Week 3 Task 3 - Factorization diagrams
Today your mission is to…
Browse a gallery of factorization diagrams below, and then make your own! Factorization diagrams show numbers in terms of their prime factors. This helps you to analyze the anatomy of numbers so you can get insights into their structure.
Ready, Set, Go
Search the web for factorization diagrams, or start with our overview of features. You have several math, art, and learning choices, for example: do you show all factors or just some? How do you tackle prime numbers? Do you always show the same factor with the same elements of art (shape, color, line, tone) or do you change the elements? Do you make your diagram straightforward or puzzling?
Count on Monsters by Richard Evan Schwartz (2003)
-
Math: Geometric (triangle for 3) and abstract representations
-
Art: Color, shape, and portraits of primes as unique creatures
Learning: Puzzling, perplexing, and unpredictable; abstract: the final quantity is not shown, just the factors

Primitives by Alec McEachran (2008)
-
Math: Nested sets show factors of factors
-
Art: Color, size, and composition of circles
Learning: Recognizable symmetric patterns, subitizing, systematic and orderly; pictures of numbers are fully predictable from smaller numbers

Diagrams by Brent Yorgey and friends (2012)
-
Math: Composite shapes (circles, polygons, fractals)
-
Art: Size, shape, compositions of small circles, color in some versions
Learning: Recognizable symmetric patterns, subitizing, systematic and orderly; color-coding has some perplexity; pictures of numbers are fully predictable from smaller numbers
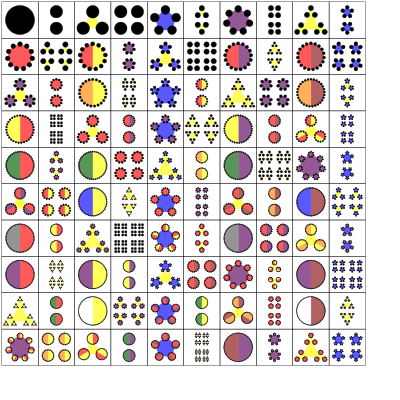
Number and letter art by Mark Gonyea (2014)
-
Math: A mix of symmetry, arrays, fractals, polygons, etc.
-
Art: Exploring one element per poster, such as line, circle, or dot
Learning: A balance of order and randomness: pictures of numbers mostly look symmetric, but are not predictable from past examples


Your forum response
- What multiplication ideas do you see in this topic? How about ideas inspired by algebra?
- Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?
How to help your child to get started
Option 1: See then make
Look at the factorization diagrams together. Ask kids to see what they notice. Accept all answers, even if they are about superficial features of the art. Ask children to find similarities, differences, and patterns:
-
Cover up a number on one of the predictable diagrams and try to guess what it should look like.
-
Find numbers that look similar. Why did the artist choose to make them similar? It may be an artistic choice, or there may be math reasons.
-
Reproduce a part of a diagram in a different medium, from Minecraft to found treasures. How does the medium influence what you do with math?
Are there numbers you would do differently? Remix some of the diagrams.
Option 2. Make then see
Invite kids to make portraits of quantities from 1 to 10, to 25, or to whatever number does not seem tedious. You may need to explain the difference between a symbol and a portrait, a number and a quantity. Portraits can be drawings or arrangements of objects, in physical or virtual worlds. Do that several times, together. Go for humour, pattern, beauty, order, and variety. Use LEGO, natural materials, found treasures, pencils, action figures, or whatever other medium your children enjoy. Take pictures as you go along. When children created some of their own diagrams and there is a pause, show them other people’s diagrams.
Toddlers
Use small numbers, up to 12 or so. Prepare beautiful stuff in just a few quantities at a time, on empty sheets of paper. Invite your toddler to arrange each group nicely, and play along yourself. You can trade object for object, but keep quantities. Your child may need to play with the stuff freely before doing that. Take pictures of arrangements.
Young children
Draw, use stickers or cutouts, use art software, make collages out of found objects. Invite kids to make connections between several numbers, for example, use the same star shape whenever the factor of five appears. Turn it into a puzzle: guess what the next number should look like from all the previous numbers. Turn it into a domino sorting game.
Older children
Explore ways to test divisibility ahead of time. For example, how do you find if a number is divisible by 3? By 5? An easier problem is to skip-count by a given number, so you find all the numbers divisible by it. Then you can use color, shape, or other elements of art to make these numbers look different, such as orange for multiples of 5 in Letters by the Number. Check out the Sieve of Erathosthenes animations. Use programming or modeling software to assist your explorations. Make the music analog of factorization diagrams: polyrhythms.
How is this multiplication?
Factorization diagrams show multiplication and division in one image. Now you see a number divided into factors; now you see factors coming together with the number.
Inspired by algebra
The most fundamental algebraic idea of factorization diagrams is reversibility. The diagrams promote the holistic understanding of multiplication and division as the reversible, connected, complementing actions.
Divisibility is the first step to building algebraic structures known as groups. Divisibility makes you focus on overarching patterns and algebraic “Whys”: numbers divisible by 4 are divisible by 2 twice over, numbers divisible by 10 always end in zero, numbers divisible by 3 have the sum of their digits also divisible by three, and so on.
Frequently Asked Question
In daily life, what are some of the very first comments we might make that can lead to more observations about multiplication?
When it comes to good chats with kids, go for:
-
Your own sincere interest. Kids sense emotions. It is okay to share fear or frustration as your emotions, as long as you are open about your feelings, and have a bit of fascination to go with them, as Blake does in The Tyger poem below. Easy start: notice something cute, funny, or nice that also has multiplication, like a kitten, a flower, or your favorite spaceship.
-
Details and particulars. These make for good stories. Easy start: make a cheat list of 3-5 particular terms that go with multiplication, for example: array, fractal, symmetry, scaling, combinations. Use these words to make your multiplication chat less generic and more detailed.
Play and adventure. Connect the conversation with children’s actions or favorite imaginary worlds. Easy start: find outdoor examples of multiplication large enough to climb, or use toys to pretend-play jumping, climbing, and otherwise adventuring in or on smaller objects.

By GapingVoid
Words
Factors, dividers, divisibility, factorization, group
Scavenger hunt
Find well-arranged quantities in nature or culture. Playing cards have groups of symbols. Windows and muffin tins come in arrays. Many folk dances, such as square dances, arrange and rearrange participants in groups that divide the total number. The children’s verse “The ants are marching one by one… two by two… three by three…” is a puzzle about different arrays made of the same ant army by different divisors.

Course links
- All course tasks
- Multiplication Lounge: our open forum for questions, comments, and ideas
- Course participants survey
People who like this
Your answer

Answer by corilewis · May 02, 2014 at 11:30 PM
Here is our picture/ diagram.

@corilewis - I love the use of color here! You may like "shape numbers" (search the web for some images). I see your kid playing with shapes of these groups.
Answer by mirandamiranda · May 11, 2014 at 04:30 AM
I love these diagrams and have been trying to figure out a way to introduce them to my children for a while. The enjoyed the video and the Primitives; we spent some time with the latter rearranging the factor order and observing how the patterns change (2x3x4 vs 3x4x2 vs4x3x2 etc...). They like the Count on Monsters book of which we have a copy, although I personally find that representation a bit less satisfying than the more abstract ones. We talked about the groups of numbers within numbers. They were not especially interested in producing their own versions.
My oldest however (8) did observe the way one of the Mike Naylor factor visualizations looked like the Eiffel Tower (looks more like a windmill to me) and drew her own. She ended up drawing mini Eiffel Towers within each branch like some of the larger numbers and we realised it was a substitution fractal! Fractals are definitely something that has come up again and again for us in this class, one daughter decided this must be why we looked at them first...

Yes, very perceptive of your daughter to notice fractals come first for a reason. They represent the cornerstone idea for multiplication: units of units (of units of units etc., if need be).
Answer by Eogruen · May 08, 2014 at 02:46 AM

This project was a big hit. We looked at the examples and the video and then each got a big piece of paper. I did mine with stickers and the girls drew. My 7 year old intuitively started asking about prime numbers. My 4 year old just drew pictures to associate with the numbers 1-5. I really enjoyed doing mine, it was just the right amount of challenge for a tired mama. Very interesting way to present primes and factors for the visually minded. I have a feeling my 7year old will refer back to this in the future.
Answer by Rodi.Steinig · May 02, 2014 at 12:30 AM
The kids loved the video - wanted to watch the whole thing.
I printed and cut out all of the factorization diagrams, and had the group examine them together. I asked "what do you think these are?" and "what do they have in common?" For the most part, the kids were stymied. One even walked away, saying, "I don't feel like doing this now." One girl did realize that the monster one represented numbers - they then thought that all of them were pictures of the times tables. Then I showed them the "primitives" online. The kids were amazed. They looked at every number up to over a hundred, and one girl looked at every number up to 1300 something. They couldn't get enough of this, and the one girl who watched it for a long time kept calling everyone back saying "you have to see this!" They were especially enamoured with the large prime numbers. Except these kids don't know what factoring is, or anything about primes. (They are beginners at multiplication.) They did notice the grouping within almost all of the number diagrams, and tried to figure out what the numbers on the right side of the screen meant (the factors). I asked again and again "Why are some of the numbers not grouped?" No one could figure that out, so I left it as an open question.
I had asked students to bring in some collections of small objects, and at this point asked them to make some of their own number tables - whatever they wanted, inspired by the diagrams. Only 2 kids did this. One other was too engrossed in the primitives online, and the other was more of a watcher. The kids who did their number diagrams, however, enjoyed it. They made visual representations of the counting numbers in planned arrangements


.
Thanks for pointing out the link to the Primitives -- I had overlooked it before. It's fascinating!
Answer by TraceySeier · Apr 29, 2014 at 12:38 AM
My kids (4.5 and 2.5) were not terribly interested in them, but all the adults who visited our house found them fascinating. I can't stop staring at them. I feel I understand the numbers better than ever before.
This is an interesting comment. With fractals or snowflakes, you see a lot of child-produced examples. All the diagrams I've seen online, as far as I remember, have been made by grown-ups. I have seen kids who could not stop staring at them... but none of the kids I've seen ever wanted to make some. Hmmm...
Answer by pkouch · Apr 28, 2014 at 03:14 AM
I showed the graphic in the domino sorting game and we made the cards. They started sorting them based on different criteria. Two of my students reached to a sorting scheme similar to what was in the blog:

They are still working on this project.
Answer by cleabz · Apr 27, 2014 at 05:34 PM
Still planning on playing with this, but one of my ideas was to use fruits and veggies, which often have a factor in them. Watermelons, when cross-sectioned, are a three and a six. Apples are a five. And so on. We play with this a lot, pointing out what number/factor we see. Then a friend on Facebook posted this, and I had to share here:
http://www.iflscience.com/plants-and-animals/mri-scans-produce-are-completely-amazing
Answer by annettehaddad · Apr 26, 2014 at 10:30 AM
My children, 5 and 7, began drawing the numbers 1-10, giving faces and legs to each. Some had hats. Then using grid paper we selected a point. Then we drew a square first by moving out one step in each direction to make it a 3x3 square. We repeated this moving out one square to make 5x5 square, then 7x7, 9x9, 11x11. We did each in a different color. Then we talked about "squares", how the 3x3 square could be called "3 squared", 5x5 would be "5 squared" and so on. They enjoyed it at the time and we will plan to add more squares to see how big we can make it.
Note: I realize the square drawing does not have all prime numbers but I used it as a starting point for drawing. Hope to build on prime number lesson.
Answer by sherylmorris · Apr 25, 2014 at 04:06 PM
I imagined asking age-appropriate children or those whose skills I know to make a design of a number's factors and having a friend guess that number. (Using Montessori beads.)




Answer by babyhclimber · Apr 23, 2014 at 03:30 PM
We loved the video shown here!!! My son immediately thought about snowflakes and element diagrams.
We had never seen the Sieve of Eratosthenes before when learning about prime numbers. Wikipedia had a cool colored algorithm of the Sieve of Eratoshenes. And we found a worksheet for making our: own http://www.mathgoodies.com/webquests/number_theory...
The most interesting for my son was polyrhythms. He is taking this one to his piano teacher tonight! http://music.tutsplus.com/articles/introduction-to-polyrhythms--audio-2573 had a great explanation and audio clips. My son is hoping his piano teacher can give him some piano polyrhythm music to try. He loved listening to the various drum ones we found and this video: https://www.youtube.com/watch?v=Zn7YtjO6Mqc
Answer by James · Apr 23, 2014 at 10:49 PM
We loved looking at the various diagrams and animations! I found this link: Prime Phyllotaxis Sprials with a neat representation of primes/composite numbers, although I admit it doesn't really deal directly with factoring. We made our own representation using music - each prime number gets its own pitch, and every number a measure to fit its prime factors into (starting with a rest so the measure numbers correspond to the represented number's factorization):

with the first 256 numbers represented here in case if you want to play around with the idea. The order and durations of notes within a measure is chosen systematically, but there's no reason not to change them up to try to make an interesting melodic line, and maybe even come up with words to match!
Answer by LeistCatalano · Apr 23, 2014 at 12:40 PM
These diagrams were a little intimidating to me at first - the remind me of IQ test - yuck!
Anyway, I did a web search, as suggested, and found these two great pages:
Animated Factorization Diagrams
I'll keep hunting around for more today.
@LeistCatalano - we may need to put a stronger warning than the word "puzzle", for people who are not into decoding. The good news is that making your own diagrams is a peaceful, meditative activity in comparison.
Love the animations in the pages you found! Thank you for these resources.
We liked the animated factorization diagrams better too!
Thanks for the links - the second one is really mesmerizing to watch!
Follow this Question
Related Questions
Week 3 Task 1: Combinations and chimeras 22 Answers
Week 3 Task 2: MathLexicon 14 Answers
Week 3 Task 4: Design by formula 14 Answers
Week 3 Task 5: Mirror books and snowflakes 11 Answers

