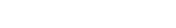Week 4 Task 1: Multiplication models bingo
Today your mission is…
Play the multiplication model bingo to see a variety of models wherever you go.
Ready, Set, Go
This is the same scavenger hunt you did during Week 1 task, What Is Multiplication. This time, invite your kids to hunt with you. Many people say they get stuck seeing the same model everywhere. Can you find all 12 models? You can print out this bingo sheet with spaces for your finds.
Your forum response
- What multiplication ideas do you see in this topic? What bridges connect this to your everyday life, sciences, and arts?
- Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?
How to help your child to get started
This activity is sort of like a scavenger hunt, only you are allowed to create your own models.

You might end up being the first who notices a particular model. Point it out to your child and connect it to an activity you did in the previous weeks. If you are stuck looking for a particular model, go through the artwork and other artifacts you and the children created over the last couple of weeks.
Find different examples of the same model. Help kids point three tips of a leaf with three fingers, hold the puppy four paws up, put feet on the two levels of a climbing structure and otherwise show numbers with bodies, as you take photos. If your child really likes a find, reproduce it in LEGO, playdough, Minecraft, paper, etc.
Frequently Asked Question
When I do these activities with my child, I feel like I need to actively teach - talk about what goes on and why. I think I’m doing too much of it though, taking over my child’s math exploration. What should I do?
You can lecture occasionally - when your child asks for an explanation. Keep it under a couple of minutes. What to do during the rest of the time? Be active, yes, but in a variety of ways: as a coworker, a naturalist-researcher, and a guru. As your child’s coworker, play in parallel: do your own experiments and explorations of the same math your child is exploring, because it creates a smooth workflow and inspires ideas. As a researcher, observe the elusive natural behaviors of your kid, take notes and photos, gently ask non-leading questions, because it will help you preserve your child’s well-being, and nurture a healthy ecology of learning. As a guru, your goal is to help kids be heroes of their own adventures. Play Yoda to your kid’s Luke.
Bob Kaplan, a math circle leader and author, says the trick is to become invisible. Active, but invisible! Read more here - http://www.moebiusnoodles.com/2013/09/becoming-invisible/
Words
Array, area, number line, set, combinations, symmetry, fractal, scale
People who like this
Your answer

Answer by annettehaddad · May 27, 2014 at 10:41 PM
My kids really loved this multiplication poster. I ordered it and had it in a corner and they keep unrolling it to look at it. They have mainly focused on the fractals, mentioning when they see something that has a fractal quality. The array and number line are others they are becoming familiar with. The others were newer and we are keeping a math journal with notes, photos and drawings to continue finding these models in our everyday lives.
Answer by mirandamiranda · May 22, 2014 at 03:58 AM
We have the poster of the models so I sat the girls in front of it (they have looked at it briefly before) and we talked about the different ways of thinking about multiplication. Some were very familiar by now (fractals, mirror books) but others they seemed unfamiliar with. We went out and had a look to see what examples we could find.
They were pretty focused on finding fractals, and immediately zeroed in on various weeds in the back yard, some which were more fractal-y than others. My oldest tried to claim that a worm she saw was an example of multiplication because it had 6 and then 4 stripes, so you could multiply 6 by 4. I suggested this should rather be addition, and she was a bit offended, so we moved on... I find it hard to be enthusiastic about all their ideas while staying accurate, just need to practice ways to approach their observation in a manner that brings out the potential multiplication. Of course now after the fact I can think of some!
I tried to interest them in some of the other models, as they were beginning to assign fractal-hood to anything with a vaguely interesting pattern. We talked a bit about arrays, amply illustrated by a Rubik's Cube that happened to be nearby. After talking about that arrays seemed to be everywhere, on book covers, peg boards, those iron-together bead things, the calendar...
We also noticed some sets, two scooters with two wheels each, and a broken chair seat with 4 rows of 8-bump springs.
The kids were not super focused on this activity to be honest. I think partly it was just happenstance, and partly the task seemed a bit overwhelming for them - so many models! Zooming in on a couple definitely helped us find a way in, I can see in retrospect that this is what they were doing with the fractal obsession.
Now that we seem to have a good handle on two or three, I am going to try and bring these up with them day to day, and gradually increase the models we notice as they get more familiar with the concepts.
Answer by Eogruen · May 20, 2014 at 01:47 PM
We did this together yesterday in the house.
Array-- decorative squares on on our door
Sets per each-- four people, two feet each
Fractals-- one of the pipe cleaner ones we made earlier in the course
Area-- the rug
Skip counting-- five petals on four flowers
Combinations-- three large dolls pair up with three little ones. My daughter was interested to find this did not equal six pairs, which was her initial guess
Scaling and stretching- my four year old very excitedly showed us this with a rubber band
Folding and splitting-- what would happen if we kept cutting their muffin for snack into halves?
Repeated addition- with Lego blocks, which led to doing symmetry, number lines with the same
Money-- how much did we pay for the splash park at two dollars a person?
Looking forward to getting our big chart!
Answer by Rodi.Steinig · May 08, 2014 at 06:34 PM
My students enjoyed looking at the chart - I don't think any of them actually realized that multiplication is more than repeated addition, despite all the activities we've been doing over the weeks! I had the 4 girls go around the house and look for examples of each model. They found and understood most, but weren't really sure about area. I don't think we had an activity specific to that in this course, unless I missed it. Each student had brought a camera in anticipation of the next activity, and each took a photo of this chart to take home. I'll email their parents the info about the poster!
Answer by mrs123 · May 01, 2014 at 09:42 PM
Here's what our family came up with. We did a photo scavenger hunt. It was surprising how many of these examples we were able to find around our house. My kids have been saying this all week--"Math is EVERYWHERE!"
Answer by perbui · May 01, 2014 at 08:29 AM
I introduced all the models right before a family trip this week, so it was fun to look for these models in contexts and locations that were out of our daily routine. We found many, some in very surprising places we had never thought of before. The thing that struck us was finding multiplication all around us everywhere! Here are only some examples:
Array: tic-tac-toe game on a playground.
Area: floor tiles at the airport.
Number line: the speedometer of a taxi cab.
Sets, per each: number of people, pairs of shoes, number of shoes.
Skip counting: 5 minutes per unit on a clock, 60 minutes per hour.
Folding and splitting: splitting our breakfast toast into pieces.
Repeated addition: counting by fives to see how many fingers we have all together.
Symmetry: looking into a kaleidescope and seeing images multiplied by 6.
Fractal: trees.
Scale and stretching: measuring relative sizes of toy plush animals.
Time and money: currency conversions. $1USD=¥6CNY, $1USD=30THB, ¥1CNY=5THB.
It's amazing to me how just over two to three weeks, my daughter's ability to observe and "find" math all around her has multiplicatively increased!
Haha, nice pun there, @perbui - it looks like your and your daughter's "math eyes" are growing! I wonder if these scavenger hunting skills will transfer to other math topics that come up in the future.
Answer by AGray · Apr 29, 2014 at 06:43 PM
This is going to be a really fun ongoing project with the kids. It was so interesting to see different kids connecting with different models. My 12 yr old is having fun making symmetry models with mirrors.
Answer by babyhclimber · Apr 28, 2014 at 01:31 PM
We played around with pictures on the internet and looking around our house & outside to come up with real life ideas for each area.
For arrays: Rubik cubes, chess board, muffin pan, egg cartons
For number line: airport runways, thermometers, measuring tape, yardstick, meter stick
http://www.mathsisfun.com/numbers/number-line-zoom... has a zoomable number line
For fractals: trees, ferns, peacocks, flowers
For area: solar panels, roof shingles, bricks on a building/tower
For set: book sets, boxed sets, deck of cards
For combinations: puzzles, Lego projects, abacus
For symmetry: snowflakes, balls, Ferris wheel, wheels, butterflies, flowers
For Scale: maps, sheet music, graphs, house plans, models of real life structures in Legos or Minecraft, model cars or trains
For time & money: clocks, watches, money in piggy bank, change counting machines
For repeated addition: sidewalk squares, counters, stepping stones, parking lot spaces
For skip counting: calculator math games (repeatedly hitting +2, +3, etc.), math charts for 2's, 5's, 10's, etc.
For Folding & Splitting: car/truck seats, origami, folding sheets/blankets/papers,
My son got more into this activity this time around now that he is has been doing daily activites of finding math in anything.
@babyhclimber, what a bounty! Good hunting there! I never thought of abacus as a source of combinations - but of course, now that you mention it, our very number system is built on them. Every place value multiplies the number of possible combinations by ten. An abacus makes this fact visible and embodied... Neat.
We had fun. My son took the assignment to mean we had to find examples in every area...LOL And he was insisting it had to be different. It was fun and definitely got us thinking outside of the box!
Answer by sherylmorris · Apr 28, 2014 at 03:44 PM
So appreciating “Becoming Invisible.” (Bob Kaplan)
“It is necessary for the teacher to guide the child without letting him feel her presence too much, so that she may always be ready to supply the desired help, but may never be the obstacle between the child and his experience.” Maria Montessori
“The most difficult thing to make clear to the new teacher is that because the child progresses, she must restrain herself and avoid giving directions, even if at first they are expected; all her faith must repose in his latent powers.” Maria Montessori
@sherylmorris, thank you for these quotes. Self-checking, choices of works, and agency-supporting accessibility are my favorite principles of Montessori design!
Follow this Question
Related Questions
Week 4 Task 2: Real times tables 6 Answers
Week 4 Task 3: Decanomial squares 11 Answers
Week 4 Task 4: Coloring the table 4 Answers
Week 4 Task 5: Healthy memorizing 1 Answer