Week 1 Task 4: What is multiplication?
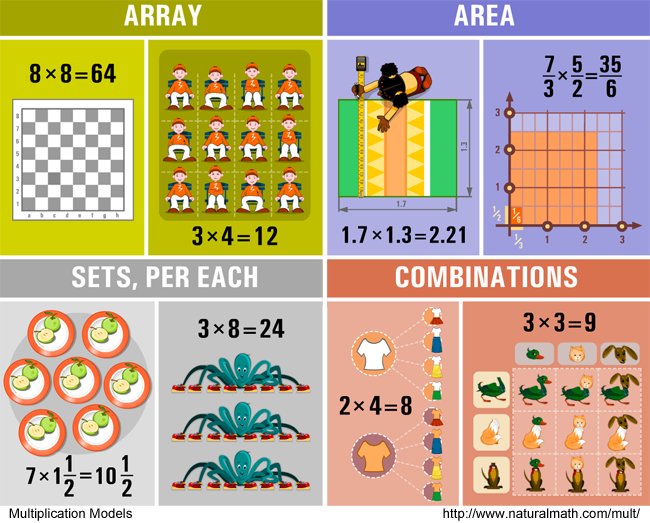
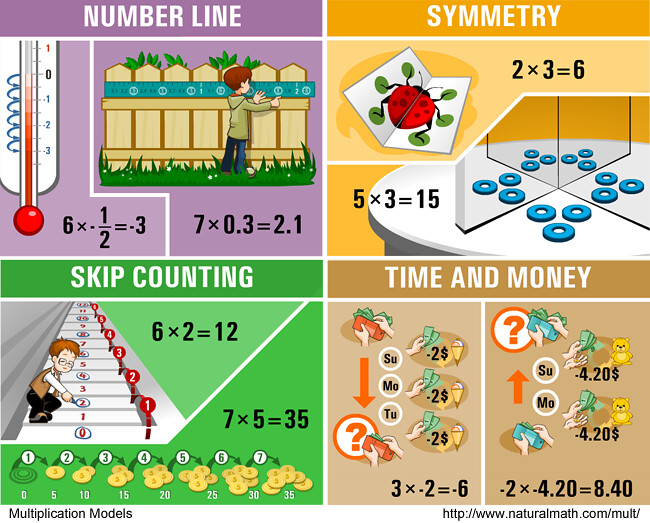

Today your mission is...
Put your math goggles on and go on a scavenger hunt for multiplication! We are not adapting this activity for the kids yet, but you can share with them any joy and beauty you find on the hunt.
Ready, Set, Go
- From the models above, select one that makes most sense to you, another one that you think has a lot of applications, and another that seems playful or picturesque.
- In the pictures, each model has two examples. Each example consists of a picture and an equation. Draw, photograph, find online, or describe in words a different example for each of your three models.
- Extra challenge: show the same equation with your three models. Can you always do this?
Why do this?
Modeling is one of the many ways to answer the question, “What is multiplication?” When adults and kids works with models, they build bridges between math concepts and beautiful, useful and personally meaningful things in their lives.
Frequently Asked Question
Is it really important to know how to do multiplication many different ways? Why three? Can’t I just use three examples of a single model of multiplication, like repeated addition?
In order to understand an idea, you need to see “many” different examples. For most people, three or more is many. And young children need even more than three. Showing many examples that are essentially the same (i.e. they use the same model of multiplication or the same delivery format) will not help a child apply the new knowledge to a different situation. This happens a lot when you breeze through worksheets, but get stumped by word problems or situations that require hands-on problem solving.
People who like this
Your answer

Answer by Elena Cook · May 09, 2014 at 12:12 AM
#1 will be Sets for me but my older children will choose "Repeated Addition" or Array
My child really liked "Head and Legs" word problems when you need to figure out the quantity of animals, so every time our trip to the zoo was about counting the sets of animals with the same quantity of legs.
#2 will be Combinations ( from a designer point of view), but my son will put it as #3
(Building a robot while looking for an optimized solution for a particular task.)
#3 will be Symmetry or Number Line
(Letters of the Alphabets/Characters in different languages-Symmetry; number line is represented by an elevator going above or below the ground level).
Answer by Jackroyd · Apr 25, 2014 at 12:06 PM
This has been an interesting exercises which I have taken my time on, making sure that I understand all of the different models. It's been quite fascinating. I haven't had a lot of time to concentrate on taking them all in which is why I'm now really behind with the course! I thought it was worth waiting until I'd understood them all though and I feel I understand the different concepts much better now.
Most sense - initially "array" as this is the model that I am most familiar with, and I felt this was very similar to "area", although with less opportunity to calculate using decimals and fractions. "repeated addition" makes a lot of sense too and this is what I use a lot with my 3 year old. Example of practical application for "array": how many new tiles need to be ordered to cover an area
A lot of applications - initially chose "area" in my more creative thought processes (cutting fabric, measuring spaces for decoration) but then went for "time and money" as a business world practical application from my pre-mummy life! Eg calculating potential earnings /losses over time for business plans and funding applications.
Most playful or picturesque-"fractals" definitely. Real life application....this reminded me of how I often get music students to remember the relationships between note values, using a "tree form" diagram (1 whole note branches to 2 half notes, which each branch to 2 quarter notes, and so on)
I managed to show the equation for working out how much you would earn over 3 weeks, working for $200 per week using the methods identified above, but I can see that it wouldn't have been easy to do this with all of the models ("folding and splitting" for example)
Answer by lisa.koops · Apr 17, 2014 at 05:34 PM
Makes most sense: Repeated addition. - Calculating how much to pay the baby-sitter per hour.
Lots of applications: Sets - silverware and tableware for setting the table.
Playful: Fractals! I've been wondering what that means every time I hear "Let it Go" from Frozen. I'll go with snowflakes - though we've had more than enough here this year.
Answer by Shannon · Apr 17, 2014 at 06:57 AM
- From the models above, select one that makes most sense to you - Sets per Each 3 chickens each of 3 different breeds (3x3), or 2 wings each per 9 chickens (2x9), or 1 comb each per 9 chickens (1x9), etc.

another one that you think has a lot of applications - Array
making sure we've made enough Valentine cards (array of 9 by 20 or 9x20)

and another that seems playful or picturesque - Combinations Love this little combination grid - 10 archetypes to cross 10 ways, 10x10

Answer by classicalmama · Apr 16, 2014 at 07:54 PM
Repeat addition: skip counting is big in our house right now. I show them when we pick up blocks for example if you pick up in 5's you get more in the basket at a quicker rate. Array make a row of pennies with 5 and columns with 5 then multiply/skip count. Sets per each cooking/plating food; 5 nuggets per person, Tator tots and 1/2cup of veggies.
Answer by TheEmily · Apr 15, 2014 at 09:43 PM
I have alway thought of multiplication as fast addition. I love how this post helped me see all of the other places I use it naturally. I use it to find out how much multiple item will cost at the store. I use it figure out the best way to stack things.
Answer by perbui · Apr 15, 2014 at 03:28 AM
Answer by scpnorman · Apr 15, 2014 at 02:51 AM
1. Repeated addition makes the most sense to me. My son might not be quite old enough to get it yet, but I can imagine dropping things into a bucket and adding them as we go (e.g. 2 cars plus 2 cars is 4, plus 2 more cars is 6, etc.). He likes processes and repetition, so I think he'd like this.
2. Folding and splitting has lots of applications around the house. When I sew II fold and cut through several layers of fabric at once, which also shows symmetry.
3. Fractals are beautiful, but they have never come naturally to me. I really have to think about one to understand how it works. It might be fun to make fractals with play dough, splitting a big ball and attaching 2 smaller ones, then 2 more for each of those, etc.
Answer by sherylmorris · Apr 14, 2014 at 09:28 PM
I had problems earlier inserting images. I wanted to share this image of a Montessori Multiplication board which has a child building an array.

Answer by yileinei · Apr 14, 2014 at 09:10 PM
Makes most sense: repeated addition. I guess it's the way I was teached how to multiply, but sometimes it isn't easy to apply, e.g. when decimals are involved.
Lots of applications: sets, per each. I think we use this everyday: putting food into plates to eat, choosing clothes for both my daughters, sharing treats...
Playful: folding and splitting. Origami games are a good example.
Answer by oxanavashina · Apr 14, 2014 at 02:45 PM
1. makes most sense - arrays/set. I went on scavenger hunt in the neighborhood, most of the multiplication examples that I registered were arrays.
has a lot of applications - sets, time&money
playful or picturesque. - fractals/symmetry
2. arrays 5x5=25:

sets 2x5=10:

symmetry 2x4=8 (or 1x2=2):

It needed en effort to get 'unstuck' from one model (in my case arrays ant sets) and at least try to see the others around.
Answer by CHabq · Apr 14, 2014 at 06:07 AM
Makes the most sense to me: Sets per each. It's the model that I can most easily and quickly picture in my mind.

Most applications: My gut reaction was combinations but after some thought, I would think lots of applications can be thought of for all the models.

Playful or picturesque: Hard to choose between symmetry and fractal so I'll say symmetrical fractals!

Seems to me that you could find equations that some of the models, whether 3 or 4 or 5 or all, would be able to show. But, maybe not all equations can be shown with each model?
Answer by jbrabham · Apr 13, 2014 at 11:54 PM
Sets of Each make the most sense to me. It may be that I was taught that way. I’m not sure. I usually introduce multiplication this way and find it easy to explain and easy for kids to understand.

3 x 5 = 15
Arrays have many applications. We organize items in arrays for ease of counting and it’s often easy to find that others have organized their “stuff” in an array and therefore making it easier for us to assess the amount. It seems to be somewhat of a natural way to organize.

Fractals seem playful and fun. They are artsy and even whimsical. I like the challenge of finding these in nature, in the grocery store, in art. I think this would be a fun exploration for students.

3 x 5 = 15
Fractals are my favorites for scavenger hunts, too! I noticed your pictures did not insert, and the path to them points to your desktop (which we can't see on the forum). Can you click the gear in the top right corner of your answer, select Edit, and then insert pictures using the Image menu, please? I would love to see them!

Answer by Reenie · Apr 13, 2014 at 02:33 PM
I am so excited we had an an opportunity to talk about scale and multiplication yesterday. My son was watching a silly youtube video which featured lots of small Lego people and one giant Lego figure. We stopped the video and measured the figures and determined the giant was three times the size of the smaller figures.
It's so sweet when serendipity like this happens! With LEGO blocks, comparing height and volume (the total number of blocks in the project) give you two different results... It's interesting for older kids to investigate these connections.
Answer by corilewis · Apr 13, 2014 at 07:37 PM
Array is what I think my brain does. I see the item grouped like that.
a different example: when I get bored (say on the treadmill) and count the ceiling tiles...
7 tiles across, 8 tiles down
An applicable one is folding and splitting. I do that all of the time cooking, or portioning out servings.
ex. strawberry shortcake. 7 people, need 8 slices, fight over that last one later.
Divide shortcake in half, then those halves in half, then each quarter in half.
Fractals are certainly beautiful.
a different example: the trees out my window.
Answer by AGray · Apr 13, 2014 at 04:08 PM
1. Sets pet each makes the most sense to me. I think combinations has a lot of applications. I find fractals really appealing and interesting!
2. We used sets to count pennies,I showed by son how to make poles of 5 and count them to find the total. I found an expletive of combinations in my 6th graders science book: pinnet squares for blood type. My daughters crochet project had a fractal pattern, in row 2 she worked two stitches into each stitch from round one and so on.
Answer by Caroline_Prochazka · Apr 13, 2014 at 11:39 AM
- Sets per each and repeated addition are the models that make I tend to fall back as easy to explain and one of the most frequent uses in my life; folding and splitting would seem to have a lot of applications; and fractals and symmetry seem most playful as they immediately inspire my creativity.
- Sets per each comes up in our lives when we pack our bags for a family trip; I use the splitting part of folding and splitting when I bake bagels, pastry or anything doughy where I want equal sized pieces so that each piece is the same; I might use fractals in a quilt design, or in a doodle, but I occasionally find one on a book cover where the picture shows a person/character is holding a book with a picture of themselves holding the book, with a picture of themselves....
- Our family has 4 people, who each need 2 full outfits for a short weekend trip; I divide my bagel dough in half, then in half again, then again and once more; My atlas shows two children standing on a model of the earth, holding the same atlas with a picture of themselves, smaller and smaller - I count 4 copies of the book shown on the front cover. In each case the math would be 4x2=8. My instinct is that one can always do this - give many examples to illustrate the same math phrase. Models may vary from commonplace to obscure, but I can't think why the rules wouldn't hold for all the examples provided.
Answer by Valerie · Apr 13, 2014 at 01:15 AM
Thanks for this question. Looking at the different ways to think about multiplication, I can see that I tend to use a few of these from day to day but I’d probably use sets or arrays approach the most. I ran through an example with my 5 year old, making different sized arrays made up of her favourite cars and using other examples such as the rows and columns of an ice cube tray. As for the most promising approach, I would say that all these approaches taught in a creative, fun way would help children to understand the concept. However, I think some approaches may feel more intuitive to some children than to others. I would predict for example that my daughter would really enjoy the folding and splitting approach but I am looking forward to seeing if this is right. We have bought an origami kit and we’re going to have some fun with that. More generally, I like the idea of using different approaches to demonstrate a deep understanding of multiplication but on the other hand I wonder if I could pull it off without confusing my daughter! I’d be interested to hear others thoughts on this. The most picturesque approach are the fractals, but it’s probably the one approach I am least familiar with. I found some lovely fractals here: http://www.coolmath.com/fractals/gallery.htm
Answer by sherylmorris · Apr 12, 2014 at 07:46 PM
More multiplication, please.
"Let's see, what multiplication stories can we find here?"
Answer by pkouch · Apr 12, 2014 at 06:49 PM
Sets: what makes sense the most
3 x 4 = 12 (three sets of four)
Time & Money: most application
Thomas earns $10.00 per hour working. If he works for 5 hours, how much money will Thomas earn?
Symmetry & Fractal: playful
1 x 6 = 6 6 x 10 = 60