Week 1 Task 4: What is multiplication?
Today your mission is...
Put your math goggles on and go on a scavenger hunt for multiplication! We are not adapting this activity for the kids yet, but you can share with them any joy and beauty you find on the hunt.
Ready, Set, Go
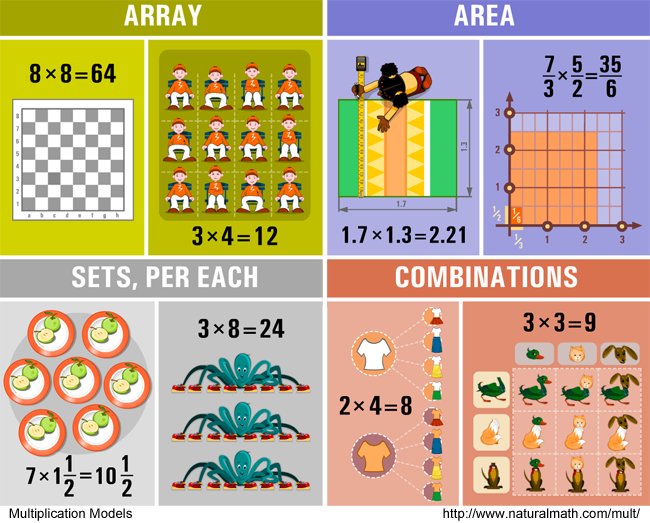
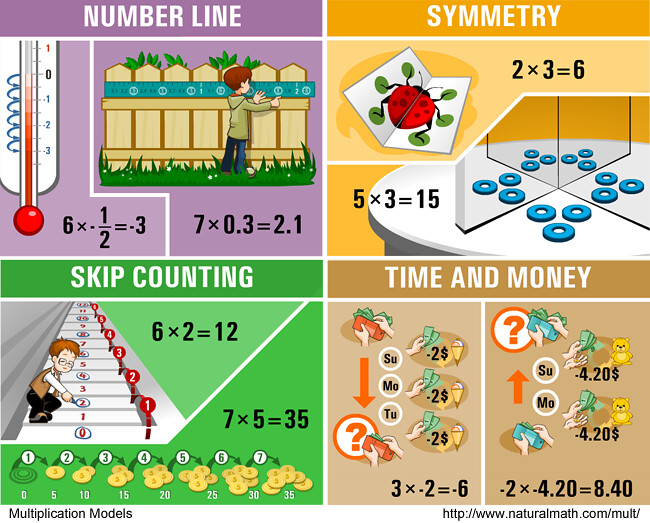
- From the models above, select one that makes most sense to you, another one that you think has a lot of applications, and another that seems playful or picturesque.
- In the pictures, each model has two examples. Each example consists of a picture and an equation. Draw, photograph, find online, or describe in words a different example for each of your three models.
- Extra challenge: show the same equation with your three models. Can you always do this?
Why do this?
Modeling is one of the many ways to answer the question, “What is multiplication?” When adults and kids works with models, they build bridges between math concepts and beautiful, useful and personally meaningful things in their lives.
Frequently Asked Question
Is it really important to know how to do multiplication many different ways? Why three? Can’t I just use three examples of a single model of multiplication, like repeated addition?
In order to understand an idea, you need to see “many” different examples. For most people, three or more is many. And young children need even more than three. Showing many examples that are essentially the same (i.e. they use the same model of multiplication or the same delivery format) will not help a child apply the new knowledge to a different situation. This happens a lot when you breeze through worksheets, but get stumped by word problems or situations that require hands-on problem solving.
makes the most sense: repeated addition. I think this makes the most sense to me because this is how I was originally taught multiplication. My example of this is getting a yahtzee! in the game of yahtzee!
Equation: 6 + 6 + 6 + 6 + 6 = 6 x 5 However, you always get a score of 50 for a yahtzee!, regardless of which side of the dice come up 5 times - so any respectable yahtzee! player will use 30 for sixes and hope for another yahtzee! Hope springs eternal...
a lot of applications: scale and stretching. My example of this is a picture of multiple shadows of a teapot, changed by distance and angle from the light source as well as by the orientation of the teapot.
Matrices are used to stretch and skew, which are two effects of the different relative locations of the light source. However, I cannot produce an equation for this! Some simple understanding of this can be found at various websites online. Look up "transformation matrix" or something similar and you will probably be able to find one that's right for you.
particularly intrigueing to me: fractals. My example is lightening - I've been interested in it since I was a kid. There are algorithms for producing simulated lightening, e.g. this one, though they never seem close enough to the real thing: http://krazydad.com/bestiary/bestiary_lightning.html
