Week 2 Task 3: Zoom and powers
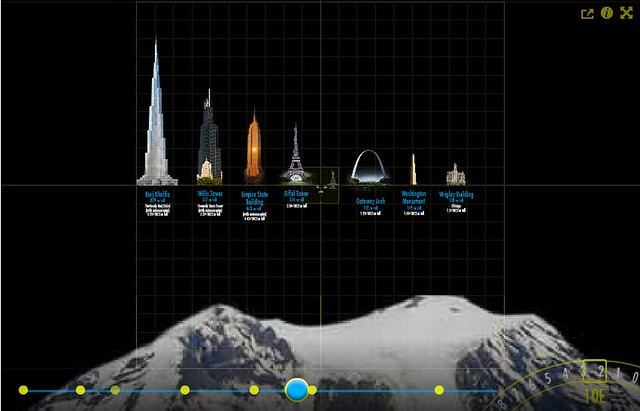
From http://www.numbersleuth.org/universe/
Today your mission is…
Explore the Universe, from its largest to its tiniest objects. Scale analysis helps us to make sense of our complex universe in terms of easy models. It lets us compare magnitudes of essential quantities.
Ready, Set, Go
Start with the powers of two, because doubling and halving is easy even for toddlers.
Trace your hand or your child’s hand on paper, and cut out the shape. This is your unit, your beginning, your 1. (The One?) Go around with this unit and hunt for other objects that are approximately the same size. You can take photos as you go along.
Now double the size - this is your 2 - and find objects that big. You can cut a piece of yarn, or a strip of paper, as long as your 2. Keep doubling your units (4, 8, 16 and so on) and finding objects of about that size. You can arrange examples of objects in a row, with the measuring units next to them. You can also halve your 1 again and again for fractional units: ½, ¼, ⅛…
You can try doing the same with powers of 10, since it’s traditional in science. Do you run out of space quicker or slower with 10s, compared to 2s?
Your forum response
Many children’s stories, such as Alice in Wonderland, feature a hero who magically grows or shrinks. Other stories have characters that are much smaller or much larger than everyone else around them, such as Thumbelina, Hagrid, The Beanstalk Giant. Reading such a story or just looking through the illustrations can be a great lead-in to this activity.
Suggest a game of pretend where you will have a magic wand that can double or halve objects around you.
Toddlers
Your hands are always with you. Keep measuring everything with one or two hands wherever you are. Encourage your toddler to estimate which objects will fit one hand or two, before measuring. Trace or print hands on long strips of paper for your 2, 4, and 8 - rather than using “abstract” strips of paper or yarn.

Young kids
Invite children to multiply or divide units of measure by ten, as they zoom from a human to galaxy and then the other way, to atoms. Use interactives to zoom:
http://www.nikon.com/about/feelnikon/universcale/
http://www.numbersleuth.org/universe/
Older kids
To fit many, many powers of the universe into one picture, invite your kids to use logarithmic scales. For example, your dog is twice as tall as your cat, but you only draw (cartoon) it one unit taller. You are twice as tall as the dog, but you draw yourself one unit taller than the dog, and so on. Here are examples from XKCD: https://xkcd.com/482/ (zoom out to galaxies) and http://xkcd.com/485/ (zoom in to strings).
How is this multiplication?
Read Addition Is Useless, Multiplication Is King: Channeling Our Inner Logarithm article for a discussion of zoom and scales. There is strong evidence that zoom and scale reasoning is inborn, but our culture so far has been imposing counting and linear reasoning. To quote:
We need multiplication, not addition. We need multiplicative number lines, not linear number lines. If we start out with logarithmic intuitions — and the evidence is strong that we do — let’s not shed them, let’s amplify them!
Read Scale Analysis: What Scientific Concept Would Improve Everybody’s Cognitive Toolkit? A favorite quote:
There is a well-known saying: dividing the universe into things that are linear and those that are non-linear is very much like dividing the universe into things that are bananas and things that are not. Many things are not bananas.
Inspired by calculus
On a hot summer day, Californians say the temperature is in the triple digits (Fahrenheit). In basketball, a double is a two-digit score in one of the five category. A great player can get a triple double in a game, that is, two-digit scores in three categories. Scale analysis gives us quick snapshots about the key characteristics of the system.
Algebra = patterns of arithmetic; calculus = patterns of algebra. Let’s look at examples of questions about zoom.
Arithmetic
A house is about 10 meters tall
Algebra
That house is one order of magnitude taller than a five-year-old kid, who is 1 meter tall.
Calculus
What height is mid-way between that kid and that house? The number which, multiplied by itself, is 10 - that is, a bit more than 3! More details in Multiplication Is King.
Frequently Asked Question
My child wants to keep going beyond the objects we can measure, handle, and fit inside the house. What do I do?
Research scales of objects online. You can usually find good examples with search phrases such as “100 meters long” or “a kilometer tall.” Or you can look up sizes of object you like, such as your favorite bacteria or planetoid, and fit them to your scale. See the adaptation for older kids for how to keep your collection.
Words
Scale, power, exponent, logarithm, zoom
Scavenger hunt
It’s time to look for examples of scaling up and down, and powers of ten. They are all around us. For example, you are carrying some powers of ten in your wallet. Most measuring devices go through at least a couple of powers. What other objects around us show the idea of scale, powers and zoom?
Watch the classic Powers of Ten video: https://www.youtube.com/watch?v=0fKBhvDjuy0
Course links
- All course tasks
- Multiplication Lounge: our open forum for questions, comments, and ideas
People who like this
Your answer

Answer by SarahKrieger · May 02, 2014 at 04:23 AM
@MariaDroujkova We kind of cheated with this the first time and used the tape measure to verify after estimating. This morning we made some "stunt doubles". When the light is less harsh I'll get some more pics.

Answer by SarahKrieger · May 01, 2014 at 06:15 AM
We used our 3.5yr old as the base measurement (she's nearly 1m tall). The door was about twice her height. Our tree is twice the height of our door. The neighbour's tree is twice the height of ours, so is 8x 3.5yr olds tall. We have been comparing objects in terms of twice or half the height since then.
@SarahKrieger - sounds like a great way for everyone to get a workout, and for a young mathematician to become the center of loving attention! Got any photos? It reminds me of a seventies cartoon "38 parrots" - press the CC button if you can't see the English subtitles.
Answer by mirandamiranda · May 01, 2014 at 04:13 AM
I did this with two six year olds. We cut out multiple hand prints, coloured them and hunted for objects that matched one, two, four then eight hands. The twin who usually has trouble getting into directed activities dived right in, while the usually compliant one sulked rather. I think this is some twin thing where at least one has to be resistant at any given time...
Larger objects were harder to find at just the right measurement. We found two sunflower plants growing next to each other, one of which was just double the height of the other, very serendipitous...


We talked a bit about powers of ten but did not really investigate. We thought about hot many hands would fit into some large items around our garden (house, skate ramp). I think this would be a good one to try again, maybe with a smaller initial unit to make multiplying by ten more manageable? I also liked the idea of using square paper.
Our string of hands is now decorating the living room which is nice, maybe it will be pulled down for more measuring.
We went on vacation to Hawaii last week and one girl asked about the distance from California to England in terms of 'doubles' of the distance from California to Hawaii (which it very roughly almost is, so it worked well). She is thinking about large distances in terms of multiples of smaller distances, and I am sure this stems from this activity.
We also enjoyed the scale interactives (especially me), but I think the controls were a bit fiddly for them to manage on their own which was a shame.
Answer by ChristyM · Apr 28, 2014 at 09:36 PM
I also showed him the video of powers of ten. He told me a couple of days later that he wants to make one too.
Answer by ChristyM · Apr 28, 2014 at 09:34 PM
Hotwheels are the toy of choice, especially for my son, right now so we used those. He loved this activity! I will try to post pictures later.
He especially enjoyed making a train of things that equal two cars. Noticing that one object is twice another object is our multiplication idea. Repeating the function leads to calculus:). I am really excited to be introducing this to my five year old. It will save so many head aches in 12 years or so.
One picture shows that two little cars equals a big car. We could repeat with two big cars. Our function would then be two cars.
Answer by Lamhita · Apr 27, 2014 at 01:51 PM
We keep going on with our math adventures but a little bit slowly ;-)
Yesterday we try your suggestiions and these are the results

one hand



Then we watch the fantastic link you provide about infinitive small and infinitive large, they were curious about size of sperm cell comparing to an adult :-)
Answer by cjmarchis · Apr 24, 2014 at 08:43 PM
I only had time to check out the number sleuth video with my husband. We were both amazed. Numbers are so powerful. We kept asking, "How is this possible?" Infinitely big and infinitely small. I'm feeling pretty infinitely small right now!
We throw around numbers like billion and trillion, without really comprehending how far apart those 2 numbers are, much less how far each is from 1. Powers of 10 are so... powerful!
I will come back to this with the kids for sure.
Answer by juggling_ginny · Apr 23, 2014 at 04:53 PM
We did this activity as part of a kitchen chemistry course we've just started. First we watched the picnic video and then had a play with the interactive zoom here http://htwins.net/scale2/. My daughter really loved this one and spent a long time playing with it, going from subatomic to universal. We haven't really covered decimals yet but she began to grasp how very long numbers can also be very small. She was also really interested in comparing the size of things in the animation. I hope to be able to go back to it at some point and ask her, 'What is 10 times as big (or as small) as this?'
Answer by Eogruen · Apr 22, 2014 at 03:17 AM

We made 1-2-4-8-16 handprint strips for my 4 and 7 yr olds. They found objects in the house and yard of those sizes. It was interesting that for both of them, the distance between their outstretched arms was about 8 handprints! Then we speculated about how tall 32 and 64 would be. This was difficult. We also discussed the step pattern made by doubling numbers versus that made by say, counting by twos, which my seven year old has worked with a lot in the past. they loved this activity and I promised that tomorrow we will cut our handprints into smaller and smaller sizes.



Eogruen, it's so interesting for a kid to notice math in herself - one of the most fascinating subjects of study! What you found surprised me, because I thought hand-to-arm ratio changes by age. You can make a life-size Vitruvian Girl times tables...
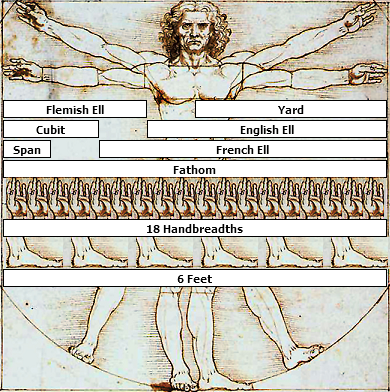
Answer by Caroline_Prochazka · Apr 21, 2014 at 01:18 PM
I am really appreciating the richness of these resources. I find the a good way to catch my 9yo son's attention is to leave the laptop open with something on the screen. This morning it was open to the text for Week 2/Task 3 and his roving eye fell on a few words, which he asked about. His question: "what is a power" led to browsing the image resources you listed. The Powers of Ten video put us in mind of another such video we had seen on the Canadian National Film Board site.
https://www.nfb.ca/film/cosmic_zoom/ from 1968, just a few years earlier. In the Power of Ten video he exclaimed that around 10E-10, the outer electrons of a piece of DNA share similarities with the image of stars and galaxies as shown in the range of 10E10 and up. We also poked around on the NumberSleuth resource with the slide bar, and talked about orders of magnitude: "the county of Isreal can be compared to the state of Illinois"...we figures about 6.5 Isreals fit into Illinois - THANK YOU background graph! And are we correct in interpreting that the area of the state of Texas is on the same order of magnitude as a cross-section area of Pluto!? The home-educating adult is getting a radical lesson, here, too:)
I asked if we could think of things in the refrigerator that shared orders of magnitude. Our list grouped grapes with olives, apples with pears and oranges, carton of eggs with bag of milk and small loaf of bread, and so on. I noticed that despite a generally high level of distraction for both kids this morning, the 9yo's range of interest spanned from the smallest atoms to the largest galaxies (we were all somewhat incapable of grasping the magnitude of the Universe!), the 5yo's range of interest went from the human sperm and egg, up to small cities and states. A good example of developmental stages, I suppose.
Leaving the laptop open is a great idea. Strewing with technology! My kids will come look when I ask to show them something, but anything that smacks of "teaching" and they turn off, eyes glazed. Watching short movies engages mine, too. Scale and comparisons are something they do naturally, but these movies and games help make them more conscious. Good idea with the orders of magnitude in food, which is much more real than Pluto and Texas. :-)
Answer by AGray · Apr 21, 2014 at 02:50 PM
My boys ages 7, 5, and 3 loved this. We traced their hands and they really got into the scavenger hunt aspect. I was surprised both how much they enjoyed it and how much trouble they had guessing what scale things around the house would be. I think they were more focused on measuring than on the powers of 3 concept.I'm going to try to introduce powers of ten next.
Answer by PruSmith · Apr 18, 2014 at 02:44 PM
I wanted to make the tasks as "native" as possible: this was quite a challenge for me as it turned out. However, the other day my 3 year old came up with the idea of measuring everything with his race car which seemed pretty close to this particular task. First we measured the bed of the dump truck toy he was using. After that we found things that were 2, 3 and 4 "race cars long" and used these larger units to measure other items. This allowed us to estimate which ones would (and would not) fit into the bed of the dump truck without having to carry the truck around with us. This seemed to make sense to him and he enjoyed the activity in a proprietary way.
I loved getting all the tasks and explanations this week! I struggle using "math" language in an accurate and meaningful way so, even without doing all of this weeks activities, this course has already been really helpful for me.
Paying particular attention to the language is one big change we implemented, compared to the earlier versions of this course. I am glad it made a difference for me.
I sometimes put up "good words" on my bulletin board and my fridge, to remember to use them more.
We need to add this idea of measuring with caravans of trucks, lined-up toy animals, and other "chains of objects" that people are likely to have at home.
Answer by Sblair · Apr 19, 2014 at 07:09 PM
We cut out two hands and calculate the area. Using one hand to measure dry erase markers, DVDs, fruit etc, then measuring both hands together going on to measure larger things we get a sense of personal knowledge of scale of ones hand but how using them can estimate how large or small an object is.
I for most think of cooking in this task. Starting out as a single person cooking for ones self, adding a spouse, then in-laws on holidays. Kids come next each time the amount of your favorite recipe increasing from the seasoning to the sheer quantity. As the children grow and find their companions, the recipe slowly increases but as holidays are frequently shared the events start to decrease and age sets in. The flow moves backwards as the children leave the home and ultimately begin again as a single person.
My sons favorite story right now is Gulliver's Travels. I asked him how is this man who looks just like the people of Lilliput so large? And how is the farm animals he takes so small too. I explain the scale factor. My daughter loved Stuart Little when she was a little girl. We are looking into homes in our new area. Using the GPS mapping to get real time(ish) photos of the area, route to work, friends and fun things to do in the area. We are explaining the zoom effect on the area and the map.
Answer by Valerie · Apr 19, 2014 at 09:21 AM
We had a look at a few videos zooming out from Earth, with the power of ten being the stand out favourite. As with the previous exercise, areas that matched her interests generated enthusiasm, such as seeing Mars (she's a big fan of H G Wells' War of the Worlds story of Martian invasion). Having the powers of ten shown on the screen whilst zooming out and back in again really helped link her understanding of simple counting with exponentiation, and also introduced negative numbers as a new concept.
We also tried cutting out rectangular strips of paper - the smallest strip was divided into 2 cells, the next 4 cells and so on. Then we found her toy cars were as long as the smallest strip, so could find out how many cars would fit in 4 cells, then how many would fit in 8 cells. After a bit of time playing with these she seemed to understand that 2 X 4 = 8.
Answer by champalto · Apr 17, 2014 at 08:55 PM
We started with random small objects - safety scissors, a crayon, a hand - and brainstormed about what item might be 10 times larger. Or 10 times larger than that! Or 10 times smaller... The video and interactive website were great illustrators of the "power" of 10, and the vastness of the universe.
Answer by Rodi.Steinig · Apr 17, 2014 at 05:05 PM
The four students (ages 9-10) enjoyed using the hand to measure, then increasing and decreasing by a power of two then a power of ten. For the power of 2 increase, by the time they got to 16 (the 5th term) they said they’d have to “hire movers” and for the power of 10, they’d have to “hire construction workers” by the third term – they “needed professionals” to gather the objects much sooner with the larger power. In each sequence, they reached a certain point where they suggested switching from a physical object to a “thought experiment.”
When we halved the units, one child wanted to rename the units (a la foot, hand, inch, etc) and the kids named ½ a dragon, ¼ a cube, 1/8 a zap, and 1/16 a slice (all names connected to objects collected).
On several occasions I called the kids back to look at what we had collected, but one child hadn’t collected an item yet. Later, when we talked about the session, she said she felt left out on those occasions. I had done this b/c of the time involved. The kids suggested that in the future, they do it as a team (instead of individual student searches) or that I give more time. I don’t think more time would have worked, though, because another student kept finding an object almost immediately then disengaged from the group by reading a book.
And J, whose house this is, was concerned that the kids were getting into her big sister’s stuff, so she suggested we place limits on where to search next time.
We kept running lists on the board of the number patterns that appeared. One student didn’t know what 1/10 meant, one did, and the 2 others figured it out immediately. For the one who didn’t get it, I showed her on graph paper. All the students watched this, and we ended up with 2 models of a unit – a paper hand, and also a 10-unit-long rectangle on the graph paper. The one student didn’t understand why the 1/10 unit of measure was a different size in each different systems – she didn’t get that fractions are ratios and not absolute numbers. I talked to her about it for a bit (using ½ of real world things instead of 1/10), but I still don’t think she completely understood.
Other interesting questions came up as this activity evolved:
- How do we use a hand to measure? (each child used it differently, but stayed consistent within their own systems)
- Why are we doing this? (to explore a type of mult. called scaling)
- How are you measuring that pillow? (One student did it diagonally and another did it by length)
- Why do we need to cut out a hand when we could just our actual hands to measure? (For that, I had no good answer at the time)
- (When we got to a scale of 100) Do we have to measure?
We did the magic wand activity, which was a fun way to wrap up this section of activities.
We looked at all the online things. The Nikon site wasn’t that interesting, and was very hard to manage in a group. The numbersleuth was more interesting. And the kids LOVED the picnic video (“classic powers of ten” on youtube). They didn’t really understand the point of the xkcd site with the drawing using logarithmic scales. They thought it was an illustration of using perspective, which is, if you think about it, kind of similar in its nonlinearity.
One student said she’d like a homework assignment of devising her own measuring system with her own units and names of things. Another said she’d hate homework of any sort. I told them nothing is required at home, but they can play around with whatever they want.
Answer by perbui · Apr 17, 2014 at 11:32 AM
I helped my 5yo son and 7yo daughter trace their hands on thick paper and cut them out. We collected quite a few items around 10-12 cm around the house after just a few minutes.

We multiplied by two, and amassed a collection of objects around 20-24 cm just as quickly.

At 4x, which was 40-48 cm, we collected only a few things, and it took much longer. They noticed right away that the nature of these objects changed considerably from the earlier two groups.

At 8x, my son gave up. My 7yo daughter continued at 96cm, but basically said that there was nothing she could pick up. They were all parts of the house's structure or furniture that was too heavy to move.
We looked at the number sleuth website to zoom in and out, starting at the level of animals because those were items that matched the length of their hands. We concluded that there are too many things in the universe that are too big for us to measure simply by addition, but that multiplication was the best way to get to those large numbers. Also, multiplication is a better way to talk about relative size or distance.
Answer by LeistCatalano · Apr 16, 2014 at 08:17 PM
I will have to try this exercise with my sons when the get home from school today. To make it simple, since they are pretty tired at the end of the day, we will look for things that are one or two hands tall. We can then discuss multiplication by 2, doubling, and halving. We may also try finding things that are one foot or two feet long.
Answer by babyhclimber · Apr 16, 2014 at 01:17 PM
OMG I had seen the Powers of Ten video in a college astronomy class and high school math class in the early 90's. Neat to share this with my son!
Of course my son enjoyed the manipulative software allowing us to zoom in & out. He equated it to like using a microscope or a telescope. And loved being able to go either in or out.
We discussed what the numbers all mean on camera lens, telescope lens, and microscope lens and better able to visualize exponents with these activities. Also viewed lots of maps and atlases in order to discuss scale and why they are useful. He found maps to be an easy way to relate to scale & power/zoom. Daddy let him play with Photoshop to zoom in & zoom out on pictures too. Some things really do look better zoomed in (insects) and some things look better zoomed out (panorama nature scenes)
I also liked the articles. I agree that multiplication is important and I think it could be taught at younger ages than typical school programs do. No need to make math seem scary. And the other article has good points on the importance of doing scale analysis.
Follow this Question
Related Questions
Week 2 Task 1: Tree fractals 49 Answers
Week 2 Task 2: Substitution fractals 24 Answers
Week 2 Task 4: Sequences and series 23 Answers
Week 2 Task 5: Multiplication towers 20 Answers

