Week 4 Task 4: Coloring the table
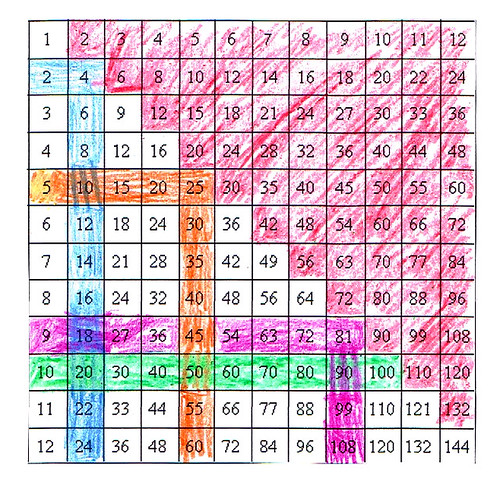
Today your mission is…
Find and color-code patterns in the times table. If you look at the times table long enough, algebra will look back at you. Instead of 100 (or 144) disjointed facts, you’ll see a jigsaw of clear, orderly, beautiful patterns. The mastery of patterns is required to be a mathematician, a scientist, an artist, or an engineer.
Ready, Set, Go
Some kids like to memorize number patterns. Others do so because of requirements. Others keep a pocket times table with them, or use calculators. This activity is designed to help all these kids, in different ways.
Invite your kids to look at the times table and color any sequence or pattern they notice. It might make sense for adults to describe such a pattern as, “A group of facts you know without any need to memorize.” Younger kids may not understand what “need to memorize” means, but they can still seek patterns. For example, there is the counting sequence 1, 2, 3 in the table; the counting sequence with zeroes behind the numbers (times ten); and the doubles, which many kids find easy, especially after activities from the past weeks. There are more exotic and hidden patterns for those who like number play. Keep seeking!
Your forum response
- What multiplication ideas do you see in this topic? What bridges connect this to your everyday life, sciences, and arts?
- Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?
How to help your child to get started
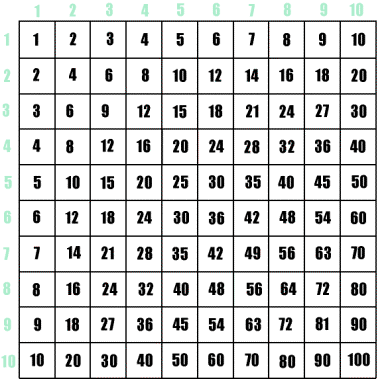
It is not necessary to reduce the table to something smaller if you work with young kids. After all, seeing more examples might help them notice the patterns. However, you do need larger cells, with numbers in large font. For toddlers and young kids who don’t yet know or are not fluent at recognizing numbers, this dot version will work. You can make your own posters using factorization diagrams.

Adapted from factorization diagrams at Math in Your Feet, Nike Naylor, and DataPointed.
It may help you to know, ahead of time, what types of patterns other people have found in the times tables so far. This does not mean you need to guide your kid to find all these patterns - let alone on the first day! This is to prepare you to expect the unexpected, because patterns come in many types. For each pattern, investigate why it works.
Patterns by the skip provide a sequence of skips that is easy on the eye.
- *10 all end in 0s: 10, 20, 30, 40…
- *2 are even numbers: 2, 4, 6, 8...
- *5 end in 5s and 0s by turn: 5, 10, 15, 20…
- *1 are counting numbers: 1, 2, 3, 4…
- *11 have repeating digits: 11, 22, 33, 44...
Personal patterns are sequences or individual facts you love and remember, for reasons of your own.
- People who like geometry love square numbers that sit on one diagonal of the times table: 1, 4, 9, 16…
- Poets love and remember rhyming or alliterating facts: six times six is thirty-six; five, six, seven, eight - fifty-six is seven times eight; five times five is twenty-five, etc.
- Psychologists note 7*8, 6*9, 7*9, and 6*8 as the facts that cause people the most confusion (see Dehaene, “The Number Sense” chapter “The multiplication table: An unnatural practice?”)
- Western musicians pay a lot of attention to *4, because many songs are in measures of four.
The symmetry pattern means that 2*5 is the same as 5*2. It makes the top right and bottom left corners of the table hold the same exact numbers, as if the diagonal were the mirror. Some people call this the commutativity pattern after the name of the property. Toddlers and young kids often like pretty math terms like this! For anyone who memorizes facts, this pattern reduces the workload almost in half.
In the nines pattern, there are many ways you can notice regularities.
- The first digit is increasing by one and the second digit is decreasing by one: 09, 18, 27, 36…
- Times nines are 1, 2, 3… away from the corresponding times tens: 09 and 10 (1 away), 18 and 20 (2 away), 27 and 30 (3 away) and so on.
- Spread your ten fingers and fold away the Nth from the left. You will see the answer to 9*N in the remaining fingers. Here’s a video from PBS: https://www.youtube.com/watch?v=Wu3JSnRaaV0
- The sum of the digits in the times nine results (up to 90) is always nine. The first digit is one less than the number you multiply by nine.
Calculation patterns are for people who love number crunching or number puzzles.
- Off-diagonal numbers run parallel to the square diagonal. They are facts like 4*6, 7*9, and in general (N-1)*(N+1). They are one less than square numbers.
- You can find a similar off-off-diagonal pattern for (N-2)(N+2), and so on.
- Times 4 is doubling, twice.
- Times 8 is doubling, thrice.
- A finger reckoning trick from 15th-century merchants, now a fun parlor trick, shows how to multiply numbers 6-9 on your hands. See details here: http://www.moebiusnoodles.com/2014/04/multiplication-a-parlor-finger-trick/

Frequently Asked Questions
Parent 1: My child believes that he is not good at math. In fact, his conceptual understanding is strong, but he’s a bit slow on calculations. Any time I suggest we play a math game or do a math activity, he just shuts down if he suspects it involves calculations. I don’t want to force him, but I do want him to be braver, and to learn how to calculate.
Parent 2: My child is overly confident, I think. Five minutes into a new activity he proclaims he’s good at it, so he’s done. He doesn’t stop to check if his answers make sense, such as 5000 mph car speed. I don’t want to lessen his confidence in himself, but I do want him to check his work, and not to be arrogant.
The two very different stories reflect the same key difference between kids and adults: metacognition, or knowing about knowing. Parent 1 and Parent 2, it’s frustrating that your kids don’t know what they know, but the good news is this is unlikely to be about character flaws of timidness and arrogance.
Use math tools to help kids grow their metacognitive skills, such as:
- Know what to check when you solve problems, where you are prone to mistakes (such as forgetting to check if 5000 mph is realistic for cars).
- Use your strengths to your advantage, pick tasks that match your strengths (Child 1 is beginning to get this awareness).
- Know your weaknesses and how to compensate for them; seek techniques, tools, learning, and helpers that can cover you (for example, using key terms from a text to seek images, if you don’t learn well from texts).
- Be aware of math values such as precision and rigor, and your personal math value system (for example, little engineers say you can’t really split a fractal into parts infinitely many times, because you have to stop at atom size, since they value realism).
- Know the size of your working memory; optimize your use of working, short-term, and long-term memory for your tasks (for example, use the partial quotient long division algorithm, which is less taxing on working memory).
Some people believe metacognitive skills can’t develop until adolescence, but we don’t think so. You can and should develop healthy math habits early on. This includes children appreciating some psychology of learning mathematics. For example, check answers after each and every problem, at all times, as a habit - but discuss how best to check for each problem. Play memory games and solve the same memory-intensive math exercises during different times of the day, so you can compare and discuss differences in how your mind works. Try to present the same problem as a picture, text, hands-on model, or whole body experience, and see which way makes sense. It will vary by problem, but some people do have favorite learning styles. In short, learn about mathematical metacognition yourself, and help your kids know what they know. Some resources to get you started:
- The Brilliant Blog
- Math Mind Hacks
- How to solve it (awareness in problem-solving)
Words
Pattern, formula, rule
- Why are waiters good at multiplication?
- Because they know their tables!
People who like this
Your answer

Answer by perbui · May 01, 2014 at 08:45 AM
My daughter noticed the a*a squares right away and colored those in first along the diagonal, then she colored each corresponding pair of rows and columns a different color, making a plaid design. Each square on the table got two overlapping colors, except for the diagonal line, which got three colors. She didn't notice any of the other skip counting patterns, like counting by 5s or 11s or anything like that. I just let her do whatever she wanted to. I printed out two of these tables, though, so next time I'll ask her some questions to see if she will find some other patterns or other ways of coloring the chart.

Answer by babyhclimber · May 01, 2014 at 12:57 PM
My kid was not into coloring the tables... He did get kick out of the parlor trick though!
As for patterns he noticed the diagonal are squares (1,4,9, 16, etc.), he pointed out that the rows & columns of the same number have the same numbers in them, he pointed out that there are more odds than evens, and that you can skip count/repeatedly add when going across each row or down each column.
Answer by LeistCatalano · May 02, 2014 at 01:09 PM
This was a fun activity for us. I printed out a stack of the times tables to color whenever. Here is one I did as an example. I colored in layers. First with the multiples of 2, then 5, then 3. The only thing left uncolored was the 1and 7's.

Answer by champalto · May 02, 2014 at 03:30 PM
My daughter was delighted to discover that the patterns need not involve adjacent numbers! She wasn't interested in coloring every square, but was quite pleased with her result:

Follow this Question
Related Questions
Week 4 Task 1: Multiplication models bingo 9 Answers
Week 4 Task 2: Real times tables 6 Answers
Week 4 Task 3: Decanomial squares 11 Answers
Week 4 Task 5: Healthy memorizing 1 Answer

