Week 1 Task 4: What is multiplication?
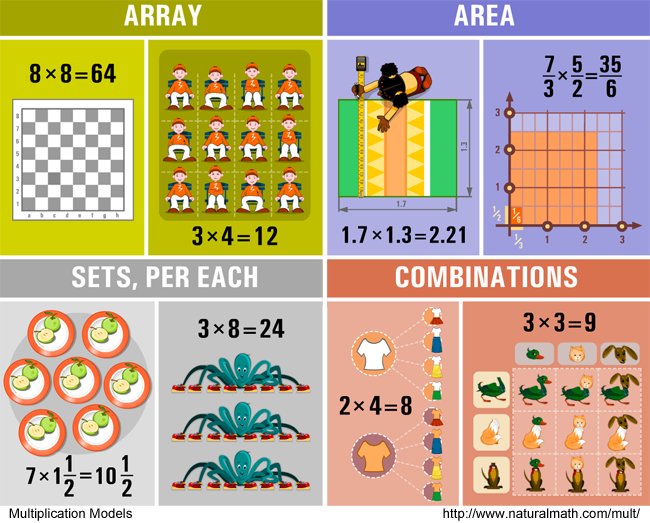
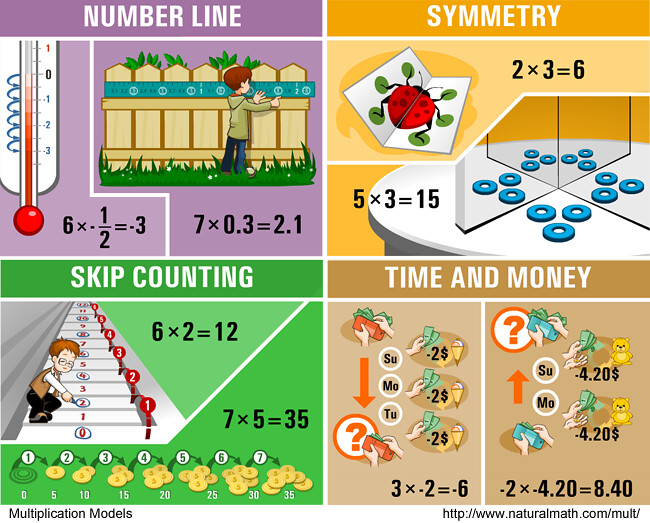

Today your mission is...
Put your math goggles on and go on a scavenger hunt for multiplication! We are not adapting this activity for the kids yet, but you can share with them any joy and beauty you find on the hunt.
Ready, Set, Go
- From the models above, select one that makes most sense to you, another one that you think has a lot of applications, and another that seems playful or picturesque.
- In the pictures, each model has two examples. Each example consists of a picture and an equation. Draw, photograph, find online, or describe in words a different example for each of your three models.
- Extra challenge: show the same equation with your three models. Can you always do this?
Why do this?
Modeling is one of the many ways to answer the question, “What is multiplication?” When adults and kids works with models, they build bridges between math concepts and beautiful, useful and personally meaningful things in their lives.
Frequently Asked Question
Is it really important to know how to do multiplication many different ways? Why three? Can’t I just use three examples of a single model of multiplication, like repeated addition?
In order to understand an idea, you need to see “many” different examples. For most people, three or more is many. And young children need even more than three. Showing many examples that are essentially the same (i.e. they use the same model of multiplication or the same delivery format) will not help a child apply the new knowledge to a different situation. This happens a lot when you breeze through worksheets, but get stumped by word problems or situations that require hands-on problem solving.
People who like this
Your answer

Answer by sherylmorris · Apr 11, 2014 at 04:01 PM
From the models above, repeated addition and sets made the most sense for me as a child; arrays and skip counting took on meaning with Montessori training and classroom experience; time and money, and splitting, I think have a lot of applications; I definitely want to play with symmetry, scale and stretching; fractals have a mysterious appeal.

1) I found the following from "Active Arithmetic" by Henning Andersen (Waldorf) Pages 80-81. It has elements of repeated addition as well as skip-counting, doesn't it?
On the floor we draw a circle, using a piece of chalk and some string, and then divide it into three as we have done so many times before. At one of the marks, we place two pupils, one on the inside and one on the outside of the circle. The teacher says “one,” and the pupil standing inside the circle runs round to the next mark. On the count of “two,” he runs to the next mark, and on “three” he is back at the first mark. Here the stationary child has his hand out, which the runner claps as he passes by. Thus we learn the 3 times table in a new way.
The next child claps hands on the count of 6, as the number-runner passes for the second time. We continue until number 10 has clapped “30” and returns to his place at the back of the queue.
Afterwards we ask the class if they can remember their number. The teacher asks Peter, who was fifth in line, which number he had, and he answers “15.”
“And you, Karen, what was your number?” Karen had number 24 and was number 8 in the line. In this way the class discovers that 15 = 5 x 3 and that 24 = 8 x 3.
Of course the class does not yet know the table “by heart,” but it does know how the tables are built up. Before we can begin to learn the tables “by heart,” there are many more games to be tried.
2) Skip-counting a handful of little plastic ants or staging the same with many children is fun for them while singing or listening to "The Ants Go Marching 3x3, hurray, hurray!"

3) An extension to work with Montessori number rods has a child making sets of little objects, 3x3.
"How many little Buddas?"
"How many little elephants?"
"How many little sunflowers?"
"How many Littles all together?"

Skip-counting and repeated addition are closely connected. We need to remix that poster to show connections between models...
Just some thoughts about the design of your poster/book art-- What if you were to use a mix of photos along with your "cartoon" graphics and have them interplay? I know that I enjoy this design approach when I see it; there are some beautiful photos here, see Eogruen.
(Please, this is not meant to criticize!!)
Answer by Eogruen · Apr 11, 2014 at 04:51 PM
The array makes the most sense to me. Can't get photos to upload, but I made 3x 3 with plastic baby toys. The sets has a lot of applications, I found five x five in the seed stars of apples I cut up this morning. The fractals are beautiful, though I don't totally understand them. My daughter and I drew a set with six pointed stars.

Array

Sets

Fractals
Beautiful! We have several fractal activities coming up in the course, so you can explore them more!
Answer by PruSmith · Apr 12, 2014 at 01:17 AM
Sets per each makes sense to me. Not sure why but it takes less effort to grasp than the other concepts. The images in the symmetry model in this case I find appealing but usually I find fractals the most beautiful. I think folding and splitting has a lot of applications (at least, this is the most common way I use or express multiplication when completing daily tasks). I couldn't come up with one equation that worked in all three cases but here are three ways to describe one of the equations in each of my chosen models.
1. Sets: Seven sweaty siblings with one and half dollars each decide to pool their dollars to buy an inflatable pool that costs ten and half dollars. After collecting the money they count it out and find 10 and half dollars exactly! 7x1 1/2 = 10 1/2
2. Symmetry: A lily growing in my garden grows 3 petals on each side of an axis down its center. When it wilts in my kitchen I dry the fallen petals and have 6 dry petals. 2x3=6
3. Folding and splitting When I make cookies I cut them this way: first I roll the dough into a long log. Then I cut it in half. Now I have two pieces. I cut those two pieces in half. Now I have four pieces. I cut the four pieces in half and now I have eight (very large!) cookies ready to go into the oven. 2x2x2=8
Math is a difficult subject for me so I've really enjoyed getting a chance to see how other people (clearly much more capable in this area than I am) have been able to communicate these concepts. Thank you to everyone!
Great examples! I could not place the warm feeling at first, but I finally remembered how as a little girl I used to watch my grandma work with dough, folding the long dough roll, cutting, folding, cutting... And I tried to help! There is something very special about dough.
What a sweet memory! Your grandma sounds like a kind soul for her to be associated with such good feelings. My oldest loves to bake with me: as soon as he hears anything clatter in the kitchen he comes running with a stool and one of my aprons to help out. He is passionate about it and gets tearful if I've made a cake or loaf of bread without him. Interestingly cooking has been the most fruitful place for spontaneous conversations about math concepts - no doubt motivated by the strong desire for our creations to taste good!
Answer by Elizabeth02 · Apr 11, 2014 at 07:55 PM
The one that makes the most sense to me is the sets one. In fact, when I first started introducing my son to multplication I would ask him "how many is 4, 3 times?" This was a strange way to say it, but the transtion to using 4 times 3 was pretty quick after that. The one with a lot of application is the Repeated Addition. Yesterday my son and I made a multiplication tower out of legos and had a blast!

(Sorry if this is huge) Anyway, the one I find most playful is the fractals image. I hope to find some fun and engaging ways to play with all of these ideas.
I am going to add this sculpture to our 2014 collection of towers. What it shows, among other things, is a big long attention span. We need those attention spans for problem-solving! I see that he took care to finish with white blocks, starting with the second layer. Neat!
To be fair, this took us about 24 hours with a lot of breaks and I suggested the white blocks, which would not have occurred to him otherwise.
Answer by Ms_Matthews · Apr 11, 2014 at 03:52 AM
All of these are 3x3=9.
For me sets are the most intuitive:

Fractals the most beautiful:

And scale must have so many applications…

Triangles as art elements - the photos go together so beautifully! All of them, not just fractals.
Answer by perbui · Apr 11, 2014 at 12:12 PM
I had some photos but for some reason I can't upload them right now. Sorry!
Makes the most sense: arrays. Anything that has rows and columns! Windows on an apartment building, bookshelves at the library, Excel spreadsheets, rows of desks in a classroom.
Lots of applications: time and money. Each week I tutor for 3 hours at $20 an hour = $60 a week. This month I tutored 12 times = $240.
Most beautiful: fractals. Snowflakes! I thought of the nautilus, too, but I'm not sure if it's a fractal or not. It's a Fibonacci sequence, isn't it?
The same equation three ways: 6 x 6 = 36
- Array: 6 rows of 6 windows = 36 windows
- Time and money: earn 6 dollars for each day of yard work times 6 days = 36 dollars
- Fractal: a snowflake has six sides, each with six little branches = 36 branches
What happens when you try to upload the photos? Is there an error message?
I bet you can connect Nautilus with fractals. It's a recursive, nested structure. Check out the Droste effect fractals: they look similar! I've never thought about it this way before, but it makes sense to me.

Answer by dnamkrane · Apr 11, 2014 at 11:07 PM
1. Makes the most sense: I'm interpreting this as "easiest way to explain multiplication", so Skip Counting and Repeated Addition fit that the best. Many applications: Combinations and Area. Most Picturesque or Playful: I'm going to go with the one that made me smile the most, and that was Fractals. 2. Skip Counting example: One book contains 11 chapters, and each chapter has exactly 15 pages each. How many pages are in each chapter? (1) 15, (2) 30, (3) 45, (4) 60, (5) 75, (6) 90, (7) 105, (8) 120, (9) 135, (10) 150, (11) 165
Combination example:
New graduate has a limited wardrobe budget for professional clothing. With 2 jackets, 3 blouses and 4 bottoms, how many different outfits can the new graduate create? 2 jackets and 3 blouses give 6 jacket-blouse combinations. 4 bottoms multiplied by each combination gives 24 possible outfits.
Fractal example: Mister and Misses Jones have three children. Each of their three children became the parents of three children. How many grandchildren do Mister and Misses Jones have? 3 1st generation children times 3 second generation children equals 9 grandchildren.
Answer by James · Apr 11, 2014 at 10:16 PM
Repeated addition makes the most sense to me (although doesn't work so well with decimals). I see area as having lots of applications. Fractals look especially interesting to me.
For repeated addition, an example is a dozen eggs - open the package, and they're arranged in a 2x6 grid. We normally use 2 at a time, so looking at the total as 2+2+2+2+2+2=12 seems to work.
For area, maybe determining the amount of wall that needs to be painted to get square footage and use that when shopping for paint.
For fractals, I've got a baby quilt I recently made that has 6 rectangles each made up of 2 big triangles, each big triangle is made of 5 smaller triangles, and each of these is made of 5 little triangles. So how many little triangles did I have to cut out to make it? 6x2x5x5=300!

To combine the three methods, let's use the quilt. Count up the number of little triangles in a medium one (5), then take 5+5+5+5+5=25 to get the next size, then 25+25=50 for the big triangle, then 50+50+50+50+50+50=300 for the whole quilt. Using area, first notice that two little triangles makes one little rectangle, which can be divided into two squares. Now count the number of squares along one edge (15) and the other (20). Total area is 15*20=300 again!
If our multiplication problem had decimals, we'd run into trouble with the repeated addition method. If the answer didn't have some of the same factors, the fractal method wouldn't work so well (or would be redundant). Negative numbers would be a bit of a stretch with the area method. So if the problem was something like -1.2 x 4.7, we'd have a challenge!
Answer by Sblair · Apr 11, 2014 at 04:01 PM

Repeated addition most application, Scale and Stretching is the most fun and Time and Money is what make the most sense.

I have my son write a draft of the information for postcards. Postcards has less space to accommodate font size and facts. Repeated addition does not always work in this scenario. In this case we had two postcard from the same city but not of the same location within the city. Most often he can write a to a few different relatives that have the same explanation.

Scale and Stretching is the most fun for us. My children love to be measured, inching up the wall. Not only can they measure there height in inches and feet but calculate the number of cm or inches they have grown within the time period noted. This works with out as long as the dates are noted.
Time and money makes the most sense for our family. We live on one income, budgeting and saving is a must. Grocery bills track easily what amount budgeted has been spent. Estimating the length of time your grocery supplies will last shows the use of the two negative amount equaling to the positive money saved for specialty items or to carry over to a time when dinner guests are anticipated.
Answer by babyhclimber · Apr 11, 2014 at 03:36 PM
1.When my son looked at the poster he immediately thought multiplication was repeated addition & skip counting but that it was also sets per each and combinations. He felt these 4 made the most sense. He said the others do make sense but that his brain does those 4 the most automatically.
2. You have to use multiplication to calculate the square footage of any room. When calculating voltages needed you multiply the number of batteries by the the 1.5 volts of the battery (6 x 1.5volts= 9volts). When you look at a fan (components inside a computer as well as floor fans) you can see fractals. To calculate the number of wood blinds you need to count how many in one and then multiply by the number of windows.
Answer by mrs123 · Apr 11, 2014 at 10:48 AM
Sets and arrays were the easiest for the kids to find. They had a blast finding these math models:
Array - buttons on our phone (4 x 3)
Sets - tea cups and saucers (2 x 4)
Number Line - Measuring cup, Coffee maker "Every morning Mommy and Daddy fill the coffee maker up to the number 4 because they always drink 2 cups of coffee each!"

Symmetry - seen in the daffodils that are in bloom right now
Scale - on a map

Answer by annettehaddad · Apr 11, 2014 at 10:42 AM
Most sense to me: sets, per each. Another example- 2 wings on each fairy. 6 fairies: 6x2=12 wings
Many useful applications: skip counting. Another ex- 10, 20, 30...yard line on football field. 10x5=50 yards in each direction from center. Two directions from center, 2x(5x10)=100
Beautiful: array. Another example- periodic table.
Answer by Brianna · Apr 11, 2014 at 08:16 AM
The two models that make the most sense to me are repeated addition and skip counting. When I was a classroom teacher- we would always brainstorm lots of things that came in groups and then write problems about them to solve in this way. Like: There are 3 elephants. How many legs are there? Or I guess this could be thought of as sets too. (Which works with Marilyn Burns' awesome Circles and Stars game. That was so fun to do with my students when I was a student teacher.)
I think that arrays has a lot of applications. I am looking at my 2 columns with 3 drawers in each column dresser right now. And my bathroom tiles. And the cookies on my son's toy cookie sheet.
For playful or picturesque- I definitely vote for fractals. As I listened to the song from Frozen today- I got a beautiful image of a snowflake crystal in my mind-- and I love this image of a beautiful repeating pattern as the snowflake extends out from the middle. (Hope I am describing this right. :o) )
Answer by KaleSprouts · Apr 11, 2014 at 03:00 AM
I find so many of the models to make sense, have a lot of applications, and be beautiful or playful. So I used today's task as a challenge to look for as many examples as I could during an outing to our local Natural History Museum and a nearby park. Here's what I was able to capture with photos:
A nice set of symmetrical objects:

An array of holes for holding crayons:

A fun combination game on the playground:

And a number line:

Answer by Nelleke · Apr 10, 2014 at 11:19 PM
I've used several of these with my son, and I'm so glad to have a few new ideas!
Makes the Most Sense: Sets. We do this with beans, as in this picture (though this is a picture scavenged off the internet... :).

A lot of applications: Time and Money, definitely. And that means that our children are naturally exposed to these all the time. We have a digital clock on our stove like this, and observing it over time has led to some realizations about multiplication: "Mama, 2 30's makes 60!" and "60 ones makes an hour."

Playful or Picturesque: Area. We play a game with graph paper, pencil crayons, and dice. He rolls two times and makes a rectangle with the numbers he gets. Then I do the same, and we see who has the biggest rectangle.

I love the fractal idea as well...I'll have to try it out soon.
Answer by juggling_ginny · Apr 10, 2014 at 09:01 PM
I love maths scavenger hunts, they really help to bring maths to life.

The array model makes the most sense to me. I like the way that you can separate the rows to give sets, or merge discrete into continuous and create area.

Sets of things - like toes on chickens - are everywhere. So many applications.

Illustrating multiplication with symmetry is fun and beautiful. I love symmetrical images, they appeal to my sense of order!
Answer by LeistCatalano · Apr 10, 2014 at 07:43 PM
Arrays make the most sense to me and are easiest to visualize. As I was looking around the house and outside today, I could see several examples already such as a dresser with 2 sets of 3 drawers for a total of 6 drawers (2x3=6).
Skip counting seems to have a lot of applications as you count off things in sets and groups (overlaps with the sets idea). I saw the row of 5 mailboxes on our street and though if each had 2 letters, we could use that to count off by twos and find out how much mail there was in total (2, 4, 6, 8, and 10 as you walk by each mail box or 2x5=10).
I also saw bunches of flowers today mostly in sets of 5, so 6 clumps of 5 flowers would be 5x6=30.
Not sure if I can tackle the same thing three ways...that's a challenge.
Answer by fcogan · Apr 10, 2014 at 05:06 PM
Area makes the most sense to me as a way of picturing the results of multiplying. Mapping, surface areas and simple things such as spills are examples of using the concept of area and multiplication. The number line concept that has numerous applications - graphing for statistical measurements, progression/regression - the use of multiples of fixed intervals to understand multiplication. Scaling and stretching is a very picturesque way of understanding multiplication - double the the height and width and quadruple the area. Scaling concepts can be taught with many materials such as playdough, rolling a pie crust, blowing up a balloon, etc..
Answer by cleabz · Apr 10, 2014 at 04:41 PM
The one that makes most sense to me is the array. Cookies on a tray, dishes I can fit in the dishwasher, and houses in a grid neighborhood. The one I find picturesque is the symmetry - I love the mirror one, and it makes me think of the mirror scene in Ramona Forever. The one that has a lot of applications is fractals. I'm watching my new seedlings grow in them, and also the tree branches outside that haven't yet leafed out. If I take 4x4, an array could be toy cars lined up in a grid; symmetry could be a ladybug with 8 spots on each side (the pictures I'm finding interestingly have 18 spots despite their name), and a fractal would be a family tree, where two couples each have two children. Fun! Going to share these examples with my daughter.
Answer by CynthiaDadmun · Apr 10, 2014 at 04:37 PM
MAKES SENSE: My 3 and 5yo are most comfortable with splitting like "If we have 12 cookies and you both share them fairly, how many do you get? What if all three of us share the cookies? What if Papa shares too?" Nothing like cookies for a concrete example they can relate to. :)

APPLICATIONS: Time and money has to be the best real-life application. I haven't used this much, but I need to find a way to incorporate it. Maybe I can pay them a penny for every minute they play quietly and let me get some work done!

PLAYFUL: Clearly the fractals. I made the name fractals for my kids this morning (http://www.edboas.com/science/ftext/index.html) and they were charmed. My 3yo said they were "zigzags" and "trees" (interesting), and my 5yo got how they worked immediately, especially after a quick google image search for "fractal" to see other examples.

COMBO: 3 x 4 =12
3 cookies for each of 4 people = 12 cookies
3 pennies a minute for a 4 minute uninterrupted phone conversation = 12 pennies
hmmm... unless I'm confused this won't work for fractals, since they are self-similar. (3x3 might but the fractal would have to stop there and thus would not be a true fractal)

