Calculus for Kids May 3, 2015 (Sundays)

Posted on May 17, 2015 by

Erin Song — No Comments ↓ Tagged with: Inspired by calculus

This is a story about the third meeting of a Calculus for Kids math circle. During these meetings, we offer children and their parents prompts, but then follow their ideas to new places. This way, children help us design!

Maria has returned from her trip to the Navajo Nation, and brought this vase. It is decorated with symbolic patterns that remind us of one of our math words: Integration. Maria asked a question about what this symbol might mean, so Allison is examining the vase to search for her own meaning.

Sometimes children fall into a curious trap; they realize they can give universal answers to many different questions. This is an excellent math principle for children to discover and should be celebrated. For example, on a scavenger hunt for hidden math, children say any object whatsoever has “a pattern” in it. Celebrate by confirming patterns are everywhere and that it’s clever to notice that. If you are looking at shapes in figures of revolution (our previous meeting), instead of seeking cylinders, castles, or flowers, children can say, “Alien spaceship” and it will probably apply to any shape. Again, celebrate children’s ingenuity by saying that alien spaceships come in all sorts of shapes – it’s just like mathematicians saying, “Shape” to mean a large category of objects.

When children overdo this, the activity becomes boring and needs to be rescued. One way to pull children out is to ask for details. What sort of spaceship? What pattern do you see? Here, Maria is leaning forward asking to hear and see Eli’s interpretation of the symbolic pattern circumventing the vase.

Let’s integrate a 3D paper spaceship out of 2D parts. Maria drew an outline of a simple rocket ship to show what we are about to create.

First, take four sheets of paper, fold them in half, and draw only a half of a rocket with the center line along the fold line. This is a nicely challenging task. Why do you draw a half? What happens if you draw the whole ship? What if you draw along the other side, not the fold line? Allison is holding the paper down so Sydney can draw easier.

Maria’s showing her rocket drawing as an example.

Then, cut along the outline of the rocket, as Eli is doing.

Maria is holding and turning the paper so Sydney can maneuver the scissors better. These types of assists help children do more with physical objects. Why do we care? Why not just cut for the younger child? Because the connection between the hand and the brain is two-way. By handling paper, children directly teach their brain about shapes and their mathematical properties. In this case, about the slope.

Next, open up the rockets and staple along the fold line. Krishnan is stapling the rocket they are making with Yash.

Once it’s securely stapled, spread the layers of paper around. This models disk integration for bodies of revolution.

Image from Wikipedia.

Spaceships look realistic enough for the shape, but do they really fly, children ask? They try, and it turns out that no, these models are just for looks.

So the group is back to the table, where Maria is about to teach them how to make a 3D paper airplanes that really fly. This is an example of how children help to redesign activities, if we only follow their actions. We did not plan to research which models fly well (and why). But, it’s a rich question that made our activities livelier.

Maria talked through every step. A lot of asides about math terms come up when you do. Here the steps are all in one place, because it’s easier to understand this way if you are reading rather than playing along with someone:

First, fold a sheet of paper in half vertically.

Then fold the top right and left halves along the middle line, forming a triangle.

Observe how children think and do things differently. One triangle is facing upward and the other downward. Which is correct? Even with simple technical tasks, there are many right ways of doing them.

Next, fold the whole triangle down – or up, if you are holding your paper the other way!

By the way, children tested their planes after each and every step! Eli tried it first as a joke when we first folded the paper in two. Maria kept up the joke and said that this “airplane” does not even fall well. Everybody wanted to try, and then they kept trying with all the intermediate steps.

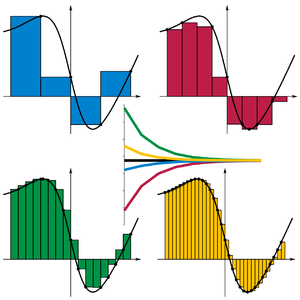
Some modeling techniques create models that get progressively better with each step. Riemann sums (above, from Wikipedia) are this way: the smaller the intervals, the better your approximation, but at each step, the approximation does work. Other modeling techniques are not progressive, and you have to wait till the very end to see any result at all. Children were experiencing that second kind of modeling with paper airplanes. They had a lot of fun with the unfinished models flying so badly that they didn’t even fall well.

Progressive techniques are used in many fields. For example, web design and image coding.

Now, fold in a stabilizer: a tiny triangular tip of the larger triangle. This way, the plane won’t wobble, but have a nice balanced flight.

Again, fold it in half symmetrically: here come the wings!

Maria is helping to fold. The next step is tricky.

Yash is about to test-fly his handmade 3D paper airplane. Sydney is still working on decorations for her spaceship. Sometimes children stay with a project longer, but they still observe others – especially their parents – doing the next one.

Maria and Sydney are flying Maria’s paper airplane back and forth and Yash keeps testing his with Krishnan.

A trick to make the planes fly better: straighten the wings really nicely.

Sydney is ready to test-fly 2 airplanes at the same time, while Maria is watching the circle flying their planes from a cozy cushion.

Sometimes things do not go the way we planned or designed – there was an airplane accident! Accidents happen even in math circles. Leaders need to be prepared to deal with sad or upset children.

The circle is about to move onto the next calculus activity: making spaceships another way. Maria is handing out packaging foam to model layers.

Ah, so soft. Sydney and Yash also assembled spaceships out of LEGO blocks.

Let’s look at the 3D paper rocket ship from the side, but integrate them from horizontal slices. From the side, the top looks like a triangle, the body like a rectangle, and the thrusters like a trapezoid.

We did not want to slice our models to see how they would look across. But Maria had fruits there. She chopped a pear horizontally (like a Fruit Ninja) and asked, “What will you see when I show you the cut?” Some children answer questions about fruit slices in 3D (a cone, a cylinder), and some in 2D, from different points of view: the side (a triangle) and the top (a circle). This is a good example of how many right answers there are for one simple question!

Maria sliced the pear horizontally, then numbered each of the four slices. Except nobody wanted numbers 2 and 3, but two people wanted number 4. We ended up creating our own number system: #1 – Sydney, #infinity – Yash, and #4A and #4B for the two boys who both liked 4.

We had a brief side discussion about naming numbers every which way – how about “cow” as a number name? Children concluded that these funky number names are more like variables than numbers.

Then children traced their fruit slices onto paper plates, cut them out, traced on the green foam, and cut out foam circles. Snacking on fruit all the way! Food makes people happy. Check out Maria’s face – yep, like a happy fruit ninja. Food makes for smoother, friendlier math circles.

The nosecone is finally integrated out of the four circles.

And later, when participants made more circles, we could integrate the whole spaceship.

Why do we care? Simpler shapes (like disks) are easier to measure, so we can build more complex shapes (like cones) out of them and measure these more complex shapes too. For example, you can approximate the volumes of cones, spheres, and parabolic antennas by slicing them into disks.