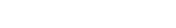Week 3 Task 1: Combinations and chimeras

Today your mission is…
Make combination tables and trees, and play guessing games with them.
Ready, Set, Go
Once you build tables and trees, hide parts of them and play guessing games. Or make a puzzle: cut the whole table apart into cells, and put it back together again. In some cases, the same cells can form many different, correct tables!
Option 1. Animal table
Your two variables are heads and bodies. Draw a cat head (or your kid’s favorite animal) in each cell of the first column, and a cat body in each cell of the first row. The corner cell will have the whole cat. Ask the child to pick the next animal. Draw the head of that animal in each cell of the second column, and the body in each cell of the second row.

Option 2. Elements of art and elements of math tables
Make a row or a column with the same color, shape, or visual symbols such as antennae for robots. Print or draw clothes for a table dress-up.

Try systematic changes from cell to cell. For example, keep adding a side to your polygons, or another eye to your monsters.

Option 3. More variables: 3D tables and combination trees
Want to use more than two variables? For color-shape-size or any other three variables, build 3D tables. Sticks and styrofoam, or yarn suspended from a cardboard grid takes you to the third dimension. A faster, easier way is to draw combination trees. You might have seen them in sandwich or ice cream shops.
Your forum response
- What multiplication ideas do you see in this topic? How about ideas inspired by algebra?
- Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?
How to help your child to get started
Help kids keep the structure. Bring up famous chimeras and modular constructs from mythology or engineering. Kids may get bored drawing similar pictures in many cells, so help them finish grids quickly. Then play with hiding cells, taking grids apart and other puzzles. Find examples of using grids for combinations in everyday and scientific media.
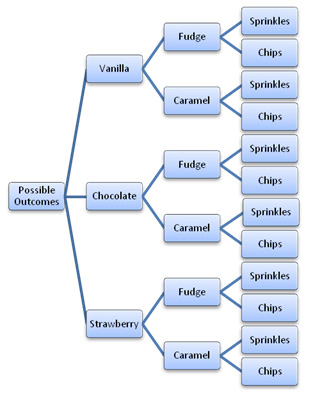
Ask “How many?” questions about combinations, which lead to multiplication. For example, a grid for three heads and four bodies has twelve chimeras total, because 3x4=12.
Toddlers
Your toddler can place cut-out parts into cells. Some kids get upset if you cut pictures of whole animals into parts, so do that step by yourself, or draw parts separately. Babies who can’t talk yet can point at toys or pictures to help you select the content of the next row or column. Toddlers and young kids often like combinatorics character creation tools in computer games, such as Hero Machine, or combinatorics toys such as Potato Head.
Young children
Kids may want to draw by themselves, or have you draw with their hand in yours. Use
different colors for different rows and columns. Children can “drive” a toy truck along rows and columns, “delivering” parts to each cell. Be prepared: between rows and columns, young children not only change the value of their variables (e.g. red, green, blue for color), but also the type of their variables (e.g. red in the first column, a hat in the second column, triangular shape in the third column). This is fine; just help kids to stay consistent within the same row or column.
Older children
As you read fairy tales or science news, keep an eye on combinations. For example, luminosity and temperature defines different types of stars, such as a red dwarf or a blue giant. Try making number tables, also called structured variation tables. Label columns and rows 1, 2, 3… and come up with your own ways of combining the labels. If you just multiply row and column labels, you will get the familiar times table.
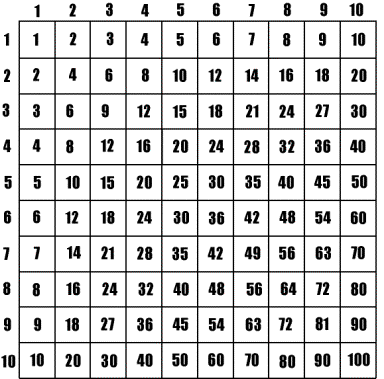
But what if you double the column label and add the row label? Or take the column label to the power of the row label? Or do something else, like the mystery table below? The possibilities for creativity and guessing games are endless! You can make these tables by hand, or program formulas in spreadsheet software.
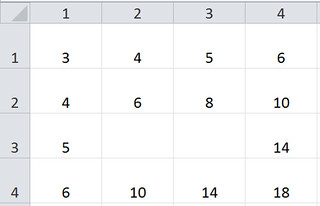
How is this multiplication?
The number of combinations in a table is the number or rows multiplied by the number of columns. In 3D tables, or trees, you multiply the number of values for three or more variables to get the total number of combinations. These visual structures model multiplication even for the youngest kids. Yet we frequently meet adults who have never perceived links between multiplication and combining different pants and shirts, or selecting bread and fillings for sandwiches. It is delightful for kids and adults alike to make this new connection.
Inspired by algebra
Combination tables and trees introduce variables: what varies from row to row, or column to column. Tables prepare kids for coordinate planes. Two tasks, “Find the point with coordinates (2, 3)” and “Find the cell with red square” mean the same algebraic action. The more subtle algebraic idea is covariation, which requires kids to notice two or more variables at once. Whenever you pay attention to both rows and columns, you reason with covariation. Kids use covariation in guessing games with missing cells in tables, or to put a table back together again when it’s cut up into cells.
Frequently Asked Question
My child is simply not interested in multiplication. Whenever I try to bring it up, show him some examples, or explain it to him, he tries to change the subject, finds something else to do, or just doesn’t pay attention. I’ve tried various approaches - living math books, board games, just plain old flash cards, but nothing piques his interest. What can I do? What if he never becomes interested in learning multiplication?
Looks like it’s time for you to move on. Some kids simply dislike some topics, and won’t learn them directly. In such a case, the child will absorb the topic from its connections and applications - if only you keep doing other, interesting mathematics. Math is not linear (even if some curricula are), so it’s very easy to skip a topic for a long while and do something more productive.
Focus on algebraic patterns, explore geometry, get inspired by calculus - there are literally thousands of math topics out there. Print out small times tables with just the results, because the patterns stand out more this way. Put these tables where you do math, for easy reference. Don’t even mention the m-word for a couple of years. Notice how our lists of words that go with activities don’t have multiplication in them…

Words
Variable, combinations, combinatorics, table, tree, covariation
Scavenger hunt
Many cultures have myths about chimeras: creatures combined from animal or human parts, such as pegasus or sphynx. Production companies from car manufacturers to t-shirt makers offer combinations of features. Hunt for words that are made out of other words, such as microphone, telephone, microscope, and telescope. Online memes sometimes feature combination tables or trees, such as alignment charts.

Course links
- All course tasks
- Multiplication Lounge: our open forum for questions, comments, and ideas
- Course participants survey
People who like this
Your answer

Answer by mirandamiranda · May 19, 2014 at 05:49 AM
This was interesting but definitely challenging for my daughters (6,6,8). We started by looking at the comics archetypes grids which I adore and they enjoyed but were not 100% on how they worked. They did like the simpler examples from you - cute aliens are always a hit!
The younger two did their own versions of the aliens, with variables ranging from eyes and headgear to antennae. We also tried out some stuff with Harry Potter characters (a current obsession) and animals. I really enjoyed making charts too!
I did copy and cut out a couple of charts to make puzzles, and there was some interest, but I think their mental energy was mostly exhausted by then.
I'd definitely like to give the trees a try, but I think I need to find a way to engage them. Ice cream flavours or paper doll outfits, I think, and a minimum of abstraction to begin with... I think we need to make some paper manipulatives.
Taking photos differently this time and they are too big - I will try and add them later.
Answer by rachelsnowden · May 10, 2014 at 04:20 PM
My son adores superheroes, so I asked him to pick four superhero toys and four villains. I asked him how many different battles he thought would be possible if only one superhero fought one villain at a time. He got really excited, and to start, I just let him start to explore with matching up the toys for different "battles" without really forcing him to be systematic in any way. I had him take a picture of each battle. After he had done that for awhile one day, I printed the photos he had taken, along with some extras of just the individual characters. I made a blank grid and then worked together with him to set it up with the heroes on one side and villains on the other. I had him fill in the pictures he had taken of battles he had already thought of as possibilities. It was actually a really great exercise for him because, in addition to the multiplication underneath it all, just starting to interact with a combination chart like this was a really good exercise for him that got him really thinking and figuring out how the columns and rows combined and lined up to show the different possibilities. Once he filled in the ones he already had (and even little brother got super excited about helping glue on the pictures and trying to predict what would go in each spot on the chart), I had him figure out what combinations were missing and use the extra character copies to fill those in.
Here is his finished chart...The pictures are really low quality, so it is a little hard to see the characters clearly, but he really enjoyed it. And, surprising to me, was that his 3-year-old little brother was REALLY into it. He hadn't even been that interested when we were doing the toy match-ups, but the chart somehow connected as an exciting activity for him.

@rachelsnowden - what a great way to remix the activity with your kid's hot interest! As for your younger mathematician, sometimes young kids are drawn to structures as such, not the story or content or objects. Try showing your 3yo Escher art!
This is such a great idea! My daughter would love this approach.
Answer by juggling_ginny · May 11, 2014 at 06:51 PM
We'd tried the chimera activity a few weeks ago, which was a big hit. The kids really loved creating weird monsters and especially liked getting parents to guess their rules. Some of the older children also tried numerical rules, mostly multiplication and enjoyed it.
I particularly liked this activity as it was a fun way to introduce children to 2-way tables which they can often find complicated.
More recently we tried branching tree diagrams to create different pizzas. Once they'd overcome confusion over why the options ended up being repeated, it led to some very productive conversations about how many possible options there were. The diagram continued to cause confusion though with some of the children still struggling to read the diagram going across to determine the toppings of an individual pizza. Still all very worthwhile though!

@juggling_ginny - there is a way to make diagrams without repeating the words. You could invite kids to create their own ways of keeping track. One way I know and like:
- Write all options on each level just once.
- Connect each option with each option at the next level
- Color-code and count all the paths from the first to the last level
This third step is hard. How do you make sure you don't lose any paths? Still, some kids prefer this option, so I should include it in the course next time around.
Answer by corilewis · May 02, 2014 at 08:13 PM
We tried this. My daughter was minimally interested. We did a 2 x2 grid of some imaginary animals and then went and looked up hybrid equine crosses, which led to looking at all of the hybrids ( odd ones) that we could find. She wasn't interested in the combination trees at all. Short interaction on this but worth a try.
Answer by Rodi.Steinig · May 01, 2014 at 06:37 PM

My students made a sidewalk chalk chimera table from their favorite animals (dog, goldfinch, turtle, then pig), figured out how to read a table, and then looked for patterns. Then they made one for pizzas (toppings and cheese types) with little help from me:

Then I complicated things by saying, "wait a minute, we have to offer people crust options - what about people who want gluten free, or thick, or (and then the kids filled in options)?" So now we had 3 variables and only 2 axis. What should we do? The kids offered and rejected many possibilities, and we left it as an open question.
We then went inside and used dolls and doll clothes to make outfit combination grids. We discussed the multiplication, and general patterns, involved. Then we did things with number grids. It was interesting for kids to see that "times tables" and "Caroline's outfit table" were the same thing, but then their interest diminished when I suggested they look for patterns with numbers only.
Answer by Eogruen · Apr 29, 2014 at 07:51 PM

My daughter happened to get a coloring book of mythical creatures this past weekend, so after doing a couple grids with colors/shapes and animals badly drawn by mom, we copied a bunch of sea chimeras and switched their tails around. Might have been more interesting if they had different types of bottoms or hadn't been chimeras already to begin with, but we still had fun! My daughters were already fascinated by the book, which is full of chimeras and they took to the idea of recombining very quickly.
@Eogruen, you rise a subtle point: is this activity more interesting if you start with "plain" objects and turn them into chimeras - or if you are in a context where magic has already happened before you came? I don't know the answer: some fantasy, sci-fi, and scientific worlds with chimeras are very, very engaging. Yet some kids love making their own worlds from scratch. It's like pretend-playing in an existing "franchise" universe vs. creating your own worlds!
Answer by ChristyM · Apr 29, 2014 at 08:16 PM
This exercise demonstrates multiplication because to factors come together to give the "answer" for each square. It also is a nice demonstration of algebra where the function (picture) is determined by multiple variables.
I started by making a grid. I asked my child to choose a color and a shape. I drew the shape in that color, then asked for another shape color combination, filling in the grid as directed. Both children were able to predict what went in the next square. One said, "This is interesting." After the pieces were cut apart, one was able to quickly reconstruct the grid, but not the other.
Answer by pkouch · Apr 28, 2014 at 02:38 AM
We used two counters, one blue and one red. I had them flip them twice and fill out the combination table:

Then, I had them follow the same steps with two dice. They ended up asking for larger papers and drawing the tree over and over again to accommodate more branches.
Answer by zzzeee2000 · Apr 28, 2014 at 12:08 AM
For me this makes a lot of sense. The meme thing is something that helps me because I understand what the characters are like and there for I understand the idea
@zzzeee2000 - exactly, with characters, you usually have a pretty deep holistic feeling for how they are, so you get a jump-start at understanding other structures involving them.
Answer by annettehaddad · Apr 26, 2014 at 10:21 AM
We made a combination tree with favorite ice cream flavors and toppings. My daughter, age 5, especially liked this. She began following the tree branches and coloring each with a separate color to represent each individual path. My son, age 7 began counting all of the paths. By the end of this week I was amazed to see my two children seated at the table with my son "teaching" my daughter multiplication! They were both so proud of themselves.
Answer by James · Apr 24, 2014 at 12:37 AM
We did musical instruments with their accessories (the glove represents a hand). Note that in this case, multiplication does not commute - playing a bow with a violin isn't the same as playing the violin with a bow (so when we study non-abelian groups in abstract algebra later, she'll be like "oh, you mean like the instruments/accessories!").
I played each combination for her, then let her choose what to play with. Two unexpectedly interesting combinations were bow/xylophone (makes a rather ear-piercing screech - didn't make any appreciable sound on anything else but the violin), and soft mallet/ukulele (with the stick hitting the strings and the head hitting the body of the ukulele at the same time). Maraca on drum was also a nice combo.
My daughter immediately went for xylophone/teeth (no, teeth weren't one of the accessories, but she's not hindered by rules), then fingernails/ukulele, then hard mallet/violin (the body of the violin, not the strings as was demonstrated to her - very individual creativity!), then an attempt was made to try teeth/violin (expensive instruments were at that point removed from the experiment), then she tried to destroy the drum with teeth and fingernails until it finally rolled away and she had to resort to chewing on the quilt.
I'm not sure she absorbed much of the mathematics, but we still had a good time.

@jwardlawbailey - this sounds like a great activity (pun intended)! I was thinking of how you can make the math of it meaningful on the baby level. I am reminded of Sim Tunes, which probably does not play on modern machines anymore. It had cute music creatures going along a grid, interacting with cells:

I imagine the columns of your table as different bars: a piece of wood, a piece of metal (like one bar from a xylophone), a hollow plastic tube, etc. I am not sure how to form rows - maybe suspend mallets, maracas, etc. from a short string on wooden sticks on bathroom curtain rings? Or place a grid from a bottle box over your bars and place a copy of the same tool in each cell in a row?

Then your table will combine different mallets and different media to bang on, in ways a baby can see. Montessori has sound toys, but I have not seen any that come in grids.
Your posts about math plus baby have all cracked me up as I have a ten month old tagging along with her older sisters as we explore this course. She has not learned any math that I know of but she has thoroughly enjoyed eating papers, trying to chew on chalk and sampling various other delights.
Answer by Valerie · Apr 24, 2014 at 11:54 PM
I wanted to do a grid ranging from slim boy slim to fat boy fat, so we could include the pop star Fat Boy Slim, but we ended up using Qwirkle. It's a great game, in which you place tiles to form lines of the same shape or colour, and we laid out all the tiles. She really enjoyed this and was able to put most of it together herself.

What a funny idea about that pop star! I can see how you can create funky paradoxes with these combinations... Or dramatic characters, like a Dark Side Jedi.
Answer by yileinei · Apr 24, 2014 at 01:41 PM
We did this and I was amazed about how quickly my daughter got it! We did 3 versions. The easiest one was the colors-shapes one, then the animals, and last the king-queen-house one because with the other two she could play. She counted how many animals we got mixing three and she was exited about how many different she could do! We put them names mixing the words: like "perrofante" mixing "perro" (dog in Spanish) and "elefante" (elephant in Spanish) (we are Spanish, thats why we did that bit in Spanish lol)



You can add the third dimension by using multiple languages! I imagine small signs with names going up in a column: perrofante, dogphant, sobakon...
Answer by TraceySeier · Apr 23, 2014 at 09:44 PM
We did Duck, Princess, Alien and Dog in chalk on the driveway. At first the 2.5 yr old just sat on the drawing, and the 4.5 yr old didn't seem to get it... then they started shouting "Alien-Princess" and "Princess-Alien", and then they drew all over the top of my pictures and laughed and laughed. They say "pretty good activity".
Answer by AGray · Apr 23, 2014 at 07:03 PM
My five year old enjoyed this! We made 3x 3 grid on the marker board and I let him pick the animals that I drew. He thought it was very funny. He counted all the combinations. These activities are great!
Answer by mrs123 · Apr 23, 2014 at 03:13 AM
My kids had a great time with this activity. Even my toddler got involved with this one. He loves scizzors and gluesticks. The girls even had fun coming up with new name combinations for our crazy version of Disneyland characters. Donkey (Donald's head with Mickey's body) and Mickdonald (Mickey's head with Donald's body) were our favorite new characters! To be honest,the idea that columns x rows = the # of combinations was a new realization for all of us, so thanks for pointing that out so clearly!

The funny thing is, even people who routinely use combinatorics in their research don't necessarily connect it to the kiddie version of multiplication! We are treating this idea playfully to make it accessible, but it happens to have very serious applications in statistics, agriculture, and most sciences. Here's a table of traditional hybrids between horses and donkeys:

Lions and tigers mix, too. Making ligers and such.
I love this!!! I forgot about a hinny... My grandma's brother still had the family farm when I was growing up and I remember explaining this to us a couple times. We used to think it was made up into she explained it...LOL
Answer by Caroline_Prochazka · Apr 23, 2014 at 02:17 AM
We started with a thorough review of the large comic times table you posted. We critiqued the art as much as the mathematical principles at play :) It got me thinking that it might be fun to make a table of sandwich toppings and imagine all the, erm, interesting possibilities. Peanut butter and lettuce, for example. But I was missing the obvious applications...read on.
The table of mix-matched heads and bodies was a hoot, too - somehow Pink Panther's body with rubber ducky's head made me think of Barbie. By the third example, though, I think the kids found it getting a little less fanciful, and straying into too much rigour (one eye, two eyes, three eyes...just not creative enough).
And so this morning, when I suggested we build a table and a tree, the theme had to be Star Wars. My 9yo worked up a table with rows showing a selection of character roles and columns showing a selection of species. We discussed how the impact of these variations would result in each cell adapting the clothing/costume/accessories of the role to the body features of the species. I'm not sure it came across in the table, and the attention span didn't last through the full table, but a point was made.

While my oldest was occupied with these illustrations, I started talking my way through a tree with my 5yo. We thought we could do a tree of species characteristics. The first branch was humanoid vs. insectoid. Humanoid then split into tall and short, then each of these into furry and hairless. Insectoid split into wings and no wings, and then legs or no legs. With this tree in place, we flipped through an encyclopedic Star Wars book to find species to fit at the terminal points. The greatest number of species fit into the humanoid, tall, hairless category (6 significant characters...and counting), while Insectoid species had only one significant character per terminal.
My older son noted that the tree form was like those quizzes in magazines (or for him, in his Star Wars books) that match your own profile with a character from a movie...(or personality quizzes, for example, I'm thinking).

I found both the table and tree activity managed to convey the idea and method without needing to be too rigorous or precise - lots of scope for talking through the possibilities. We also talked about how the tree form lends itself to a choose-your-own adventure book model.
Again, this series continues with success - I am getting engagement from the kids for up to an hour a day on 'math'.
Do you think the slogan, "Rigor and precision - not on the first date!" is too risque?
Game designers use tables and trees like that all the time. Here is the species-class table from Star Wars: The Old Republic, for example, though less artistic than yours:

For example, Chiss Ascendancy people only work for the Empire for the in-universe historical reasons, and are not Force sensitive. Humans do everything, as is traditional in game design.
Fantastic - I will share this with the boys...perhaps leave it open on the laptop (strewing with technology, as it was dubbed by another commenter). And yes, rigour and precision are a little too much for my boys on a first encounter, but then later they tend to be sticklers for detail.
Answer by babyhclimber · Apr 21, 2014 at 08:37 PM
My son informed that there are chimeras in minecraft: cow+mushroom=mooshroom, spider+skeleton=spider jockey, chicken+baby zombie= zombie chicken, skeleton+wither boss= wither skeleton....
We discussed man-made chimeras in terms of fruits, vegetables, plants, dogs, cats, and animals. People purposely mixed species to get a new one or a hybrid.
We also looked at pictures of chimeras from the Ukraine at http://www.tripadvisor.com/LocationPhotoDirectLink...
And we discussed chimeras from ancient greek mythology.
Chimeras are a way to create new combinations in just about anything.
In your mystery box my son thinks its missing the number 8 & 11. First row adding 1, second row adding 2, and 4th row adding 4, so third row adding 3.
Thanks for the tips on minecraft chimera! Will send the kids to explore that, next.
Answer by perbui · Apr 22, 2014 at 05:49 AM
Another laugh inducing activity! We started out with colors and made the following plaid. My daughter noticed patterns: pure colors, same combinations, etc. On the multiplication table, these would be squares (yellow x yellow) and the commutability of products resulting from the same two factors (yellow x blue = blue x yellow). We noticed how the way she ordered the colors changed the pattern on the table rather than just following the traditional multiplication table.

We then did an animal table. We talked about variables, co-variables, and combinations, and then played "hide and seek" games. This was her favorite part! We also cut up the table and reconstructed it, noticing how there were multiple ways of putting it back together. We noticed that unlike the colors and numbers, commutability was not the same. A lion-snail is not the same as a snail-lion. I think the next time we revisit the animal table, I'll ask her to reconstruct the whole table after supplying her with three or four of the answers. She loves puzzles so I think that would be fun for her, too!

LOVE the idea for creating plaids - my son was really into drawing plaid for a while last year, he might find this amusing. And those are some sweet chimera cartoons, too.
Answer by dnamkrane · Apr 22, 2014 at 03:59 PM
We went with pizza combinations. We came up with 6 different crust possibilities, 4 cheese, 6 sauce and 7 toppings. I had to stress that we could only have one of each, and that for this exercise that was a good thing.
We started by listing out possible pizzas, then I showed them a partial tree graph, starting with crusts then branching into sauces, then cheeses, then toppings. I couldn't even fit all the options on one page! I explained why we multiplied the number of options, then one of them did the calculations in his head and the other checked on the calculator. They both got the right answer: 1008 possible pizzas!
Of course, this would have been easier to illustrate with fewer options, but when you ask two nine year olds for input, stuff happens :-)
Follow this Question
Related Questions
Week 3 Task 2: MathLexicon 14 Answers
Week 3 Task 3 - Factorization diagrams 12 Answers
Week 3 Task 4: Design by formula 14 Answers
Week 3 Task 5: Mirror books and snowflakes 11 Answers