Week 2 Task 1: Tree fractals

Today your mission is...
Make your own fractal to admire one of the most common multiplication models encountered in nature, and the incredible exponential growth.
Ready, Set, Go
Sketch an object or shape that you or your children like. Let’s call this shape the base. Mark the points that stick out, such as the tips of cats’ ears (two), vertices of a triangle (three), or ends of a star (five). Draw smaller versions of the base at each of the marked points.
Mark the same points on each of the smaller versions, and draw even smaller versions of the base at each of these points. Repeat the process as many times as you want. You justmade several levels of a fractal! Fractals of this type are called tree fractals.
Respond to today's task
- What multiplication ideas do you see in this topic? How about ideas inspired by calculus?
- Did you use this with kids or students? How did it go? What did they say and do? What questions did they ask?
How to help your child to get started
Get some paper and colored pencils and find a spot where your child can observe you drawing. Talk about what you are doing: “I drew my favorite flower, a daisy. Now I am marking little dots at the top of each petal of the daisy. And now I am drawing smaller daisies growing out of each of these dots.” Invite your child to draw this way too.
Younger children might want to start with something really complicated. We had a four-year old who insisted on drawing an excavator. Go for it! Draw it, but talk about how many “points that stick out” you will need to mark.
Your child might not want to draw, but instead might prefer to observe you do it. Enlist your child’s help with other tasks - choosing colors for each new level, marking points that stick out, and making sure that you do not miss objects.
Toddlers
Small number of branchings (two or three) are easier. Help your toddler remember to draw every part of the picture. Use colored dots, removable stickers or even raisins to mark the places where the next level of pictures goes, or invite your child to do it. Math and art variety keeps kids engaged and invites their own experimentation. For each following level in your tree fractal, try to change the color, scale the shape to be bigger or smaller, rotate it, or reflect it upside down.
Young kids
Offer your child to use software, such as http://www.geom-e-tree.com/ (iOS, has a free version) or http://www.visnos.com/demos/fractal (computer browser). You can use the software to play, or to plan large-scale artistic projects.
Older kids
Play with predictions and estimations. Which tree is easier to draw, with two or with three branchings? How many pictures will we need to draw at the next level? What level has 8 pictures? When will the tree “branches” overlap? What happens to the shape of the tree if we scale pictures up from level to level?
Shift questions towards actions instead of words. For example, if you are using stickers, leaves or building blocks to make a fractal, ask your child to prepare enough objects for the next level. Another idea is to ask your child to point to the level where a certain number of objects would fit.
How is this multiplication?
Everyone does it! Ancient Babylonians did it in base 60. Ancient Mayans did it in base 20. We do it in base 10, unless you are a computer programmer, who does it in base 2. Our number system groups quantities by powers (repeated multiplication by 10s), like levels in the tree fractal with ten branchings. This repeated, recursive multiplication is an incredibly powerful (pun!) idea with profound effects on technology and history, from Egyptian pyramids to modern computers.
But our modern number system has a major drawback: it is very abstract. It’s been developed by adults, for adults. Fractals to the rescue! Making a fractal gives us an opportunity to touch and feel the abstraction, to feel every aspect of modern number systems - the base, the recursion of multiplication, and the sequential arrangement of powers.
Inspired by calculus
Fractals give kids a practical, hands-on recipe: how to make an infinity. The infinity kids make with tree fractals is easy to imagine and to understand, because it’s easy to make and to see. But this easy infinity comes with a more complex structure than, for example, just stairs that go on and on and on. It has built-in ideas of exponential growth, scale, and orders of magnitude. The stair (linear) structure is artificial, but fractal, recursive, nonlinear structures are everywhere in nature.

Algebra = patterns of arithmetic; calculus = patterns of algebra. Let’s look at the example of a doubling fractal tree, called binary tree.
- Arithmetic
-
How many pictures are at the next level of the binary tree, if this level has 4?
-
2*4=8
-
Algebra
-
What function gets you to the next level of the binary tree?
-
f(x)=2*x
-
What is the speed of growth of that function?
f’(x)=2
When you draw tree fractals, you mostly act at the calculus level, because your main decision is how to branch the tree.
Frequently Asked Question
Ok, so now my child can make tree fractals. But how does it help my child get better at actually multiplying anything?
There are two direct benefits of fractals for calculations. First, they give kids the hands-on, embodied access to the structure of our number system, as we explain above. The second benefit is more subtle: fractals give a big boost to children’s ANS, Approximate Number System, which is one of the cornerstones of successful calculations. Such visual, well-organized patterns help kids to picture the quantities (say, at each level of the fractal), which helps the skill of estimation. Here is a recent study about ANS, explaining why 5-year-olds can (and should) work with algebraic patterns. Like fractals!
Then there are the soft skills of math. Building even the simplest tree fractal is challenging for young children, because they have to be able to keep a pattern going, and because there is a lot of work. The mistakes are easy to notice, though. This way, kids develop the mathematical values of precision, rigor, and perseverance.
Words
Fractal, scale, power, exponent, binary, recursion
Scavenger hunt
Start with the art above, and talk with your children about trees as the lungs of the Earth. Trees and lungs and corals have the same branching structure of tree fractals, and for the same reason! They are maximizing the surface area within a given volume for super-efficient gas exchange.
Watch this slightly spooky video of a fractal hand:
Can you find other examples of fractals in nature, architecture, technology, crafts and art?
Course links
- All course tasks
- Multiplication Lounge: our open forum for questions, comments, and ideas
- Course participants survey
People who like this
Your answer

Answer by juggling_ginny · Apr 18, 2014 at 08:12 PM
We looked at this kind of fractal as part of a maths circle session on doubling and halving a little while ago. I started by reading the myth of Hercules and the Hydra heads. Even though my circle is all girls, they were immediately excited by the chopping off of heads. They were all competing with each other to calculate how many heads would be on the next iteration. Later on in the session we drew square based fractals on squared paper and triangle based fractals on isometric paper. Using grid paper encouraged a greater level of accuracy, with the necessary calculations, but became a bit overwhelming for the younger or less able children - although they could quite happily devise colouring schemes for other people's fractals.
We finished by watching Vi Hart's binary tree video and were really inspired by the crashing Hydra heads doodle. When faced with a boring half hour (like waiting for me to have my acupuncture session) this is still my daughter's favourite activity. She's had numerous goes at it and has improved in accuracy and consistency each time. Really looking forward to trying some more fractal activities with her.
Answer by Joyce · Apr 18, 2014 at 06:25 PM
My 12 year old daughter and I did a few different tree fractals, drawing shapes on paper. What was really neat about it is how easy that made thinking about powers of any base. When we used a five pointed star it easily led into a discussion of repeated multiplication and then powers/exponents of a single base, 5. Such an elegant introduction! We also discussed the idea of infinity and whether we could add up all the areas of our stars.
Answer by Sblair · Apr 18, 2014 at 12:58 PM
echer.jpgMy son (9) thought the fractal hand video was a little spooky also. However it got him to think of infinity. We started with the definition of fractal then the Sierpinski Triangle. We did a chalk drawing of the triangle that then led to infinity. We did simple addition and I explained the power of multiplication. We tried a carrot drawing and I explained the importance of single points that branch out to make fractals. I explained it by drawing stars and looking at our tree in the front yard.
We then looked at some of the art by M.C. Esher.
Answer by mrs123 · Apr 18, 2014 at 03:04 AM
My kids (6,4) also thought of the lyrics to "Let it go" when I told them about fractals. When I showed them how snowflakes were fractals they became so excited that they now understood what Elsa was singing about! They were not that interested in drawing them on paper, but were very interested in the apps and watching "Fractals-Hunting the Hidden Dimension" documentary (only bits and pieces of it because it's targeted more toward adults) showing fractals in nature and how they are being used in animated films, technology and medicine. They were much more enthusiastic about drawing them with chalk on our driveway. They also have been enjoying looking for fractals in nature in our yard/park or even while driving around.
One request: While you have provided great ideas and instructions for the activities, I was wondering if, along with the assignment you could provide a short lesson/paragraph/script or even a REALLY, REALLY SIMPLE way of explaining what fractals/scale/sequences etc. are to younger children. I've been trying to explain it to them using my own words and videos/pictures, but since I don't have a strong background in math, I'm not so confident that I'm explaining the ideas clearly (with words they understand) and accurately.
Answer by Valerie · Apr 18, 2014 at 02:12 AM
We started with a scanned picture of one of her favourite Octonauts characters, and made this into a simple fractal, although this was beyond the capabilities of a 5 year old. Then she had a go at the geom-e-tree app on the ipad, which allowed her to play with fractals interactively. I pointed out how the numbers grew at each point, which didn't seem to generate much interest - she seemed most interested in collapsing the fractal structure down into a single branch, then unfolding it, or changing the pictures that the fractal was made from. I didn't push the explanations with her - I thought it better to just let her explore and absorb it visually, which will hopefully help lay the foundations for developing an intuitive feel for multiplication.
Answer by annettehaddad · Apr 18, 2014 at 12:00 AM
I drew a fractal of the Easter bunny - in both directions - tree fractal style outward and substitution, using the eyes as the spot for repeating pattern. I didn't say anything to my children (ages 5 and 7), but just left the drawings mixed in among the other books they were reading. Boy did it stir up excitement! They were laughing, trying to figure it out, shouting "what is this? Where did it come from?" , counting how many faces they saw. I just casually said "oh, they are fractals". Then they started seeing the patterns and relationships and discussing among themselves. When my husband came home from work they grabbed the papers running to him "daddy we have fractals!". I can't believe the excitement this generated and we haven't even begun to discuss them.
Answer by oxanavashina · Apr 17, 2014 at 08:12 PM
I thought a fractal out of Cuisenare rods would be good for a start, but my timing was bad - too late in the day, so nobody except of me was impressed :) Next day my elder son was drawing chalk fractals - I just threw the idea in, he did the rest:
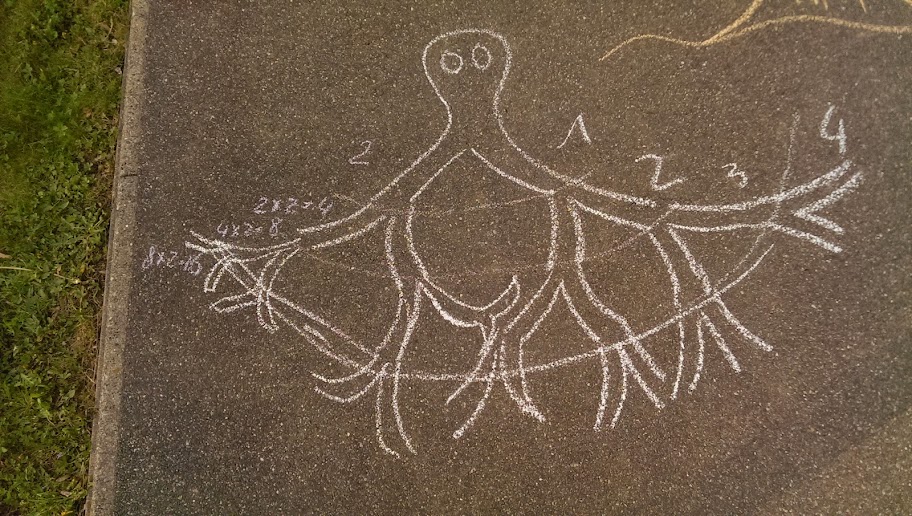

At some point he stopped drawing and started asking himself how many branches he would have at next level. A rare occasion of him asking a math question, so I shut up and listened.
The younger one (5yo) didn't have much interest in what I was showing, so I am yet to find the object he will be interested in multiplying in this manner.
Answer by Kristin · Apr 17, 2014 at 05:19 PM
I started out by drawing fractal triangles. My daughter wasn't really interested because she "has done this before." What sparked a little interest was showing her the other kids drawings. She then drew fractal bunnies. She became more interested when she realized the fractal patterns in nature. We then looked at Interactive Math virtual manipulative generate explore fractal tree www.visnos.com and a Mandelbrot video this really caught her attention with her exclaiming "now I am really interested!" We watched both the Deep Mandelbrot Zoom and The Mandelbrot Set the only video you need to watch. She was fascinated and is now outside searching for examples of fractals.
Answer by mirandamiranda · Apr 16, 2014 at 04:51 AM
Wow I feel really inspired by all the comments on here! I want to just carry on making fractals with my kids all week... We have lots of forks at the moment for some reason so I might give that one a try. Although thinking about it not sure we have 16+ so maybe not!
I was working with my children, ages 8, 6, 6 and 21 months. We started off with me demonstrating a fractal triangle, then a bunny head. Then the girls had a go at drawing their own. We had a person, a dog with floppy ears, a flower, and circles. I asked how many points a circle had, and they said zero (or infinitely many? I wonder now) but my daughter just decided to add two, then four on another example, because she said that would fit.

I found they were less interested in making perfect fractals with each layer complete than in seeing how many layers down they could get.

We talked about how we could keep drawing for infinitely long, ie fractals can continue infinitely. We also talked about how the numbers of each unit increase at each level, and the size decreases. We did have some trouble with 'mushing', as someone else so eloquently put it!
We looked at the hand video and at Vi Hart's binary trees:We liked the reference in the video to the hydra's heads as one daughter has a Heracles obsession - we talked about how the heads (which grow two in place of each one that is severed) would grow like a fractal tree.
We had a bit of a go with the ipad app, my oldest was interested but not enough to look for more than a little while. My 21 month old however loved it, although not sure how much that was general ipad love as he is not usually allowed on it!
My oldest then found a fractal weed of some kind outside in the garden.

Thanks for the suggestion of allowing kids to colour in our designs, by the way, all my girls enjoyed that:

All in all a great activity, although they did keep saying fraction instead of fractal which could get confusing...!
PS I hope my images come through ok as I have not posted any before! So apologies if not.
Sorry the link for the Vi Hart video is https://www.youtube.com/watch?v=e4MSN6IImpI
Ahh, you copied your bunnies for kids to color? Interesting! This way, you can experiment with color as a separate variable.
Your images came through, and I made them visible. If you want them to show without people clicking the link, use the Insert Image button that looks like a photo of some mountains:

That pictures with many layers down is a type of fractal too! After the first level, that fractal tree only has one branching.
Fraction, fractal, fracture - kids see similarities over differences. All these words do come from the same root! If you and the kids like words, you can go on an etymology scavenger hunt.
Thanks Maria for the image tips - I will try this next time! And I wondered about the 'fract-' root - definitely a good one to discuss.
Answer by dnamkrane · Apr 16, 2014 at 10:55 PM
My 9 year olds are at a sleepover, so I tried this out with my 14 year old.
I kept it simple and went with a triangle and then a square. The first level was one triangle, the second level was three triangles, and after that it got more interesting: the third level was six triangles, the fourth level was twelve triangles, the fifth (not drawn) would have been 24, etc.
I asked my daughter to describe an equation for the levels using 3 and 1. For 6 (level three) she said "6=3x(1+1)". I proposed an alternate: "6=3x(3-1)". She wanted to know why it made a difference. I tried to guide her to it with 12 (level four) with the same rule to use 3 and 1, and her first answer was "12=3x(3+1)". Again, I proposed "12=3x(3-1)(3-1)", but she still wasn't buying it.
I drew a square fractal: level one was one square, level two was four squares, and again, things got interesting after that. Level three was 12 squares, level four would have been 36 squares, level five 108 squares and so on.
She immediately recognized that 12=4(4-1), and also ended up arriving at 36=4(4-1)(4-1). When I asked her why, she said because the equation was simpler than 4(1+1+1)...and then she couldn't wait to leave.
The equation for a "regular" n-sided polygon-fractal after level 2 seems to be n(n-1)^(level-2). The rate of change or f'(x) would be n-1 for those levels, but n between level 1 and 2. Would love to know how to express that as a calculus equation.


Answer by CynthiaDadmun · Apr 16, 2014 at 05:58 PM
I worked with my 5yo on drawing fractals and that was good:

But what was really awesome was seeing his reaction to a youtube video that continually zooms in on the Mandelbrot set:
https://www.youtube.com/watch?v=ohzJV980PIQ
Totally blew his mind. (Mine too for that matter). After that, we spent ten minutes watching a documentary with Benoit Mandelbrot talking about it (before his attention span wavered) :)
https://www.youtube.com/watch?v=s65DSz78jW4
I'm not sure the multiplication part is coming through (although we talked about that with the triangle fractal), but wow this stuff is good ammo for making math cool and exciting!
Answer by AGray · Apr 16, 2014 at 02:21 PM
I love this assignment! I've always been interested in fractals, but not too sure how they connect to multiplication. I tried drawing a cat fractal with my 5 yr old, but he wasn't too interested. I think the drawing intimidated him. I'm going to try again today.
Answer by champalto · Apr 15, 2014 at 03:07 PM
My 6-year-old had fun creating the"frozen fractals" from the song "Let it Go!" She is also excited with the thought that our body has fractals!

I have not seen this technique before. So dramatic! I bet it would look gorgeous on glass, maybe a window.
What a great idea! I'm going to let her do it on a window. It's Crayola Model Magic - that would work easily. And the icicles would match some of the ones we have outside! :)
Answer by perbui · Apr 15, 2014 at 06:02 AM
I showed my 7yo daughter fractals on paper using triangles, flowers, stick figures, stars. When it came time for her to do it herself, she took the easy way out and did it with lines. She said, "It's easier this way." However, she did get into the artistic component of the assignment by using colors of different hues and values, starting with dark valued colors for the base and getting lighter as she moved to the edges. She commented on how fast it took to run out of room and have the branches run into each other.
We talked about exponents, exponential growth, sequences and series. We connected it to a project we did last year on infinite series reaching 1 (half of half of half of half...), and determined that tree fractals are infinite series reaching infinity. (Is that right? I don't know enough calculus to wrap my brain around that.)

Yes, this series adds up to infinity - the term for that is divergent series.
What a beautiful minimalist design, and color-coding! A lot of the times, kids choose simple design when they are focusing on the abstract, pure math aspects of the situation. Little engineers, artists, mathematicians, and philosophers approach the same task differently!
The number of lines diverges, but not necessarily the length of the lines, depending on how much shorter you make the lines at each iteration. If the lines in each iteration were a fourth as long as the previous, the total length would be 1+2/4+4/16+8/64+...=1+1/2+1/4+1/8+... which might look familiar. So you could have an infinite number of lines but only need one crayon, one piece of paper, a whole lot of time on your hands, and the ability to relax the laws of physics that only allow things to get so small.
If successive iterations only got smaller by half, you'd get 1+1+1+1+..., which would go up to infinity. If you were to try to draw all the iterations, I think you'd get lines overlapping, and the wax of the crayons would get thicker and thicker — you'd eventually need a ladder to draw the next iterations, then you'd have to take the roof off your house, then you'd need a helicopter, then you'd need a spaceship, then you'd probably get bored of drawing tiny iterations and go exploring with your spaceship instead.
Answer by sherylmorris · Apr 14, 2014 at 09:18 PM
I wanted to experiment making tree fractals with Montessori beads. I had difficulties with "crashing" and then materials ran out.


------------------------------------------------------------------------------------------
The way leaves (or cones) can represent an entire tree is actually appreciating fractals. Yes?
Unfinished artwork (below) frames in an area where I keep a nature plate. Children who visit are allowed to explore. I listen for comments like, "Look the leaf is a tree." I don't go into lecture mode, I may simply say, "Oh, you noticed that!" I like creating environments where children can learn or realize things on their own. I believe that they are more inclined to "own" it, more so than when an adult tries to "pour" information into their heads.

I'm hanging my tree fractal this time. When I work with these, I'm impressed with how quickly multiples increase. ty

Answer by James · Apr 15, 2014 at 05:09 AM
We made a "forktal" (well, I made it while my daughter watched - she's not much help at 6 months old). We counted the tines on one fork (4), made a big fork out of four forks (with a knife as a handle), and counted the total tines (16), and noted 4*4=16. Then we made an enormous forks out of big forks, and calculated the tines at 4*4*4=64. Next we made a ginormous fork out of enormous forks (we had to break out the plastic forks partway though construction), getting 4*4*4*4=256 tines. I asked her what would happen if we had another 3 tables with similar setups, and we calculated 4*4*4*4*4=1024 tines. Perhaps more interestingly, I noted that our table had 4 iterations, and a normal fork has 4 tines. What if we did the number of iterations in a ginormous fork? $$4^{256}=1.53\times 10^{154}$$ would be a lot of tines! Actually, even if all the mass in the universe was converted to forks (even really small ones!), we wouldn't have enough to build this rather large fork. Imagine that instead of 4 iterations or even 245 iterations, we used the number of tines in this new rather large fork... How many times should we keep upping the number of iterations before we have an unimaginably large number?

What a story! I like the part about the mass of the universe. The Forktal reminded me of this:

Answer by TraceySeier · Apr 15, 2014 at 07:44 PM
We tried just drawing tree fractals with my 2.5 yr old and 4.5 yr old. The favorite was an ice cream sundae fractal where each cherry had a new sundae put on top of it. We also tried cat, car, and truck. The kids seemed to understand that each layer had smaller objects, and more of them. They didn't seem to get the multiplication aspect of it, but overall, they said "it's pretty good".
Answer by Eogruen · Apr 15, 2014 at 02:01 AM
My 7 year old and I played with fractals a few days ago and Today we drew one with chalk outside and then she played with the app for a good 20 minutes. I think she understands the idea, we will keep playing with it this week. I love the idea of making one of beads. We might try that!

Today we made fractal trees with beads and pipe cleaners. I made mine two branches up to 32. My daughters pooped out on three branch trees at nine branches, but then my 7 year old made a tree of pipe cleaner dolls!
Answer by babyhclimber · Apr 15, 2014 at 03:12 PM
My son enjoyed playing with http://www.visnos.com/demos/fractal. Right away he noticed it was going by multiples of 2. He started doing them 2, 4, 16, 32, 64 (which is minecraft block limit), 128, 256, etc. He pointed out its the same language used in processing and binary code. He also played with writing it out as exponents. We then used today's activity as a challenge to make a fractal in both Scratch & Minecraft. We found someone else's Scratch program http://scratch.mit.edu/projects/1360458/ for making fractals but we also made our own. http://www.fractal-explorer.com/minecraftbasics.html gave us a start for fractals in minecraft. Our son chose to make one with redstone lamps & wool. Fractals are fun according to my son.
Would your attach your programs here, using the Insert File tool that looks like a paperclip? Scratch also has an easy uploader you could use. Or screenshots. I'd love to see!
We are having massive problems with our online Scratch program. We got it to run the program earlier just fine but now that we've gone back to re-run it and try to share it only to have the sprite disappeared and not draw. The only thing working is the exponent counter/multiplier. So you see the numbers getting exponentially larger but no drawing. My son thinks its my computer so he is trying to fix it on his and we'll see if we can get it to work properly. We are trying to figure out if its an issue with our computers or the scratch program. Playing with the Scratch program in the link I posted early is very cool. My son's was more of an exponentially increasing drawing of lines than a fractal tree. Disappointed that we can't get the program to repeat... On the old scratch (not web based) which we can't share he can't get the sprite to show but does get the drawing. I admit to not being a scratch expert so hoping daddy can help fix it when he gets home.
Answer by Caroline_Prochazka · Apr 15, 2014 at 02:54 PM
We started out with the spooky hands, followed by an easy hook for the ids: YouTube videos (sadly, kids, there is no hits for 'Star Wars Fractals'). There are some nifty computer graphic rendered fractal videos to be found - many are quite hypnotic. While watching we came up with words for what we thought of these fractals - repeating, growing, patterns, infinity, Universe, swirling.... Then we took it to pencil and paper and sketched some models (stars, lightning bolts, squares)...getting simpler and trying to find how to have the fractal fill more space and less space, and overlap itself more or less. I sent my fidgety 5yo to the fridge to hunt for a fractal (cauliflower), which he then observed under a magnifying glass. Simplifying to a tree fractal, we drew models of base 2, base 3, base 10 (looks like a dandelion, they said) to explore the difference in how quickly the numbers grow. I introduced my 9yo to the idea of base 2 (binary) for computer language and base 10 is what we know as the decimal system. His mind was blown when I noted some Ancient systems used base 20 or even base 60 - neither of us could quite wrap our minds around the scale of either of these. When enthusiasm for the pencil/paper activity waned, I got out the iPad with Geom-e-Twee and they each explored the binary and ternary tree fractal modeling in that mode for another while. My 5yo was most interested in stretching and scaling. My 9yo was interested in the effect of swirling finger movements to make a kaleidoscope effect, and had fun identifying all the shapes that came together - squares, 3Dish boxes, snowflakes, conifers, hearts and many more. By then I needed a break. What high paced exploration! I offered them a challenge: head to the playroom and see if you can build some sort of fractal idea from lego bricks. Curious what they will come up with.



Caroline, thank you for sharing your process and how everyone felt - it will help other families and mixed-age groups to organize their activities!
Base 60 sounds exotic, but we still use it a lot - directly from the ancient Babylonians to our modern clocks!
Follow this Question
Related Questions
Week 2 Task 2: Substitution fractals 24 Answers
Week 2 Task 3: Zoom and powers 22 Answers
Week 2 Task 4: Sequences and series 23 Answers
Week 2 Task 5: Multiplication towers 20 Answers

