Pi is calculus (for 5 year olds): Natural Math newsletter 3/14/15

Subscribe and read archives
Pinterest | Twitter | YouTube | Facebook | Google+ 

In this newsletter:

• Three awesome activities where Pi is calculus (for 5-year-olds) – happy 3/14/15
• March 27-28 MoSAIC: Mathematics of Science, Arts, Industry and Culture (Raleigh, NC)
• Work or volunteer for Natural Math

Celebrate Pi Day with calculus-inspired activities for the young and the young at heart

Happy 3/14/15 – and let’s hope you read it exactly at 9:26 for even more digits of Pi! Here are three activities for celebrating with your children and friends.

It’s a triangle! It’s a square! It’s a… circle?!

You will need a lot of straight thin objects about the same length: twigs you find outside, pencils on a blanket so they don’t roll, craft sticks, or simply strips of cut paper. Make a triangle out of your sticks. Add one more stick – you get a square. Add more sticks – you get a pentagon. Keep adding sticks. Pretty soon, you (better – your kids!) will marvel out loud that your shape is now a circle. Is it really a circle? Engineers say “Close enough!” and mathematicians say “No way!”

• Where is Pi? Do like the ancients. Measure the length of your stick, multiply by the number of sticks, and divide by the diameter of your circle (which you measure too). You get, and I quote the engineers, close enough to Pi – the ratio of the circumference to the diameter.
• Where is calculus? What you did here is approximating a curve with straight lines. This is a step in many calculus algorithms for integration, differentiation, and limits.
• A fun twist. Instead of sticks, use kids sitting on the floor, feet-to-behinds. It’s a great photo-op for a math circle – literally!

Three and a little bit

This is perfect for young children who are starting to fall in love with numbers: “Mom, what is a million?” Or those wishing to feel with their own hands where Pi comes from. You will need yarn, tape, or anything else you can easily unfurl and cut. Find a hula-hoop or a pot lid, or draw a large circle. Measure it across with your yarn and cut – that’s your unit (the diameter). Invite your child to estimate how many such units will fit around the circle.

Keep measuring out and adding units around your circle. Three should almost cover it, but not quite! Make an extra unit, and ask your child what part of it would fit into the space that is left around your circle. Will a half fit (fold your unit in half to show)? How about a third? Find a fraction small enough that it fits the gap. But if there is a bit more of the gap left, you can estimate that with a fraction of your fraction, and so on.

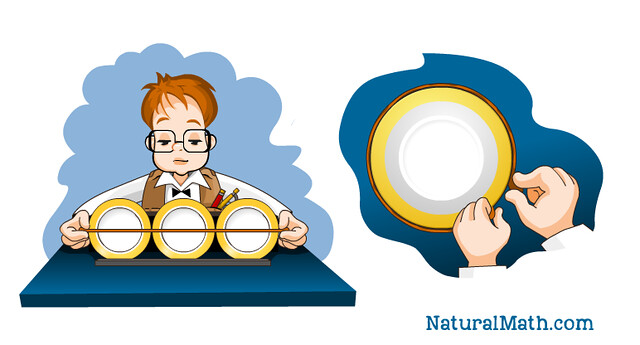
• Where is Pi? You are approximating Pi with diameter units. Start with three units, then add some piece of a unit (maybe 1/6 or 1/8), then add a smaller piece (maybe 1/4 of the piece you had before) and so on.
• Where is calculus? A mathematician claims that if you do your measurements very precisely, you will get an infinite series of fractions! Because Pi is irrational, your series will never end. Infinite series are a staple of calculus. But an engineer will say you’ll cover the circle completely in just a few steps, because your yarn measurements are approximate.
• A fun twist. With older kids, try dividing your unit (your diameter) into tenths, then those fractions into tenths, etc. You might see that the circumference is about three units, one tenth, and four hundredth… Pi = 3.14… but you may get slightly different values depending on your precision.

Pi=4

This is a teen or grown-up party trick. The steps are so simple a five-year-old would get them, but to enjoy the punchline, you do need to know what Pi is.

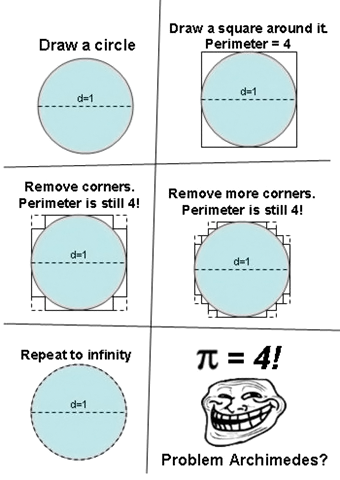
• Where is Pi? Well, we found Pi, and it’s apparently equal to four. Engineers like Archimedes who just approximate everything – beware! But wait, aren’t our previous two activities all about approximations? Were they all wrong too?! (No, they just happen to be okay.)
• Where is calculus? This intriguing piece of math trolling demonstrates that in the calculus world, things aren’t always what they seem. Taking a limit can easily go very wrong. Vi Hart has more to say. https://www.youtube.com/watch?v=D2xYjiL8yyE
• A fun twist. Could you use other shapes to “prove” Pi equal to other numbers?

For more young calculus, check out the Moebius Noodles collection!

MoSAIC Festival in Raleigh March 27-28

MoSAIC: Mathematics of Science, Arts, Industry and Culture is a festival celebrating the connections between mathematics and the arts. The festival will take place March 27-28, 2015 and it is free and open to the public. It is a great opportunity for children and adults to experience and reflect about the interplay between math and art, and for parents and teachers to find inspiration for student activities.

Join the Natural Math crew

We are growing. Join our adventures!

Part-time paid positions

• Lead math circles and courses. Help us meet the demand for family activities in the Raleigh-Durham, NC area, or lead online courses for families and teachers.
• Scout the web for young adventurous math. Want to seek young algebra and calculus around the web and blog about it? Want to look for innovative math circles and write their stories? This job is for someone who loves to browse the web, connect with interesting people online, and to blog.

Volunteer opportunities

Spend quality time with engaged people working on meaningful mathematics! You can volunteer as little as an hour per month. Our current volunteers include teens, parents, university researchers, software developers, retired professionals, social media activists, and creative writers. This is perfect for people who want more active but casual engagement, or want to ramp up their skillset and resume.

Email maria@naturalmath.com to talk about work or volunteering.

See you online! Dr. Maria Droujkova and the Natural Math crew