Calculus for Kids April 17, 2015 (Fridays)

This week was all about Flatland. Download the Math Spark that invites you to travel to Flatland with us.

Before new activities, we sat and reflected on what math we had noticed last week. Check out what we call “mathematical faces” – when children think about mathematics, their faces look special.

“Sometimes, these thoughts can make me gigglish!”

Maria is taking the tools (papers, sticky notes…) out for the hands-on creative activities on the table. Do your children have trouble transitioning into activities? Make it a ritual to set the table for mathematics with colorful materials, and whatever you need to feel good – snacks, drinks, and toys. Rituals like this give children time and a framework for transitions.

Maria:  “Look at this 2D hairband.  It is curved but also can be straightened out.”  We can manipulate some 2D surfaces to be either flat or curved.

Priyesh cut out a 2D shape (bound by curves) for his football project.

Maya is in the process of making and playing a 2D orchestra – two drums so far, a circle and a square.

Maria is listening to the story of Owen’s project: his (2D) coffee filter represents a (3D) ice block with cuts representing cracks. We use black or bright construction paper for dramatic backgrounds to models. It helps with storytelling.

Maria is about to show how to make a shape similar to Owen’s with just one cut of a (folded) coffee filter.

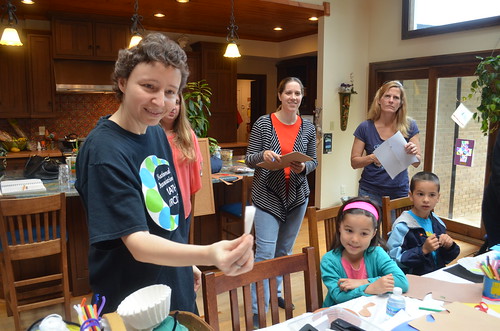
“What do we have here?”

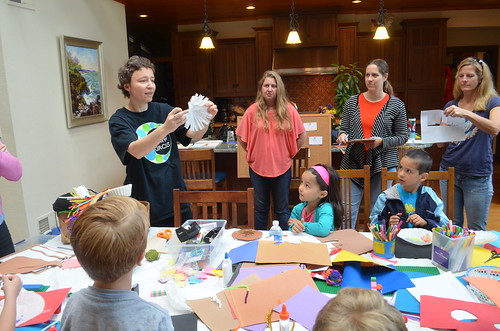
Another example of how a 2D flat paper can turn into a model of a 3D spiral snake.

Charles is making a random 2D decoration for his wall, with each piece uniquely, irregularly shaped. Another math or art term for random shapes is “abstract.”

For his next project, Charles triangulated a turtle-bobcat, then added dots for more regularity. This is similar to a technique from Australian Aborigines.

Lori constructed a curved shape (a circle) arranging LEGO blocks that are straight squares. Then she commented how the shape becomes smoother and the triangular wedges between the squares become smaller when you use more blocks. You get a more precise approximation of your circle with a polygon that has many, many sides.

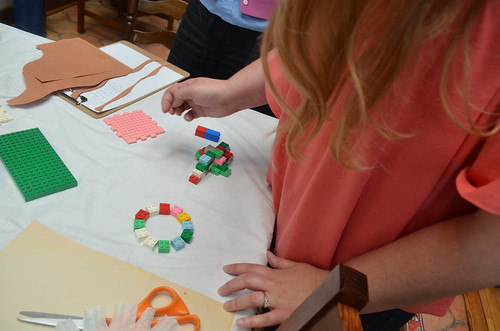
Can you cut a hole in a piece of paper that is large enough for you to fit through? Amy shared a way… Besides, you can use the resulting zigzag to form curves, like a big goofy smile or a circle.

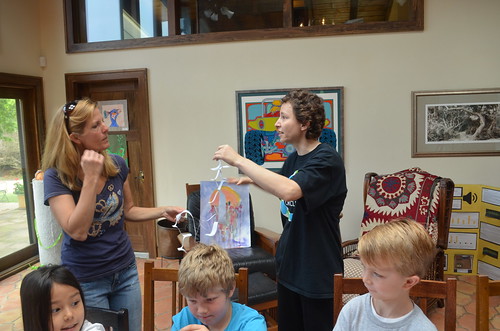
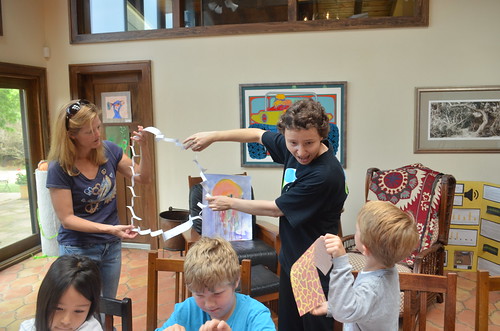
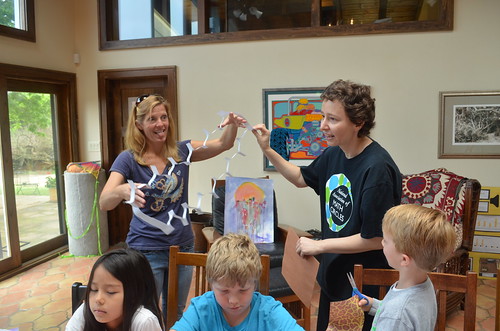
Now that the 2D ring is cut out and formed, let’s see if we can go inside the ring!  First comes Serrin.

Then, Eashan…

…Finally, Maria sneaks in for a photo-op.

Eashan is busy making a mosaic of a waterfall (2D, curved) out of sticky notes (also 2D, but straight).

Maria is showing a 2D face Serrin made with 1D details out of pipe cleaners (very curved).

“Can your eyebrows curve like this?!”

Our eyebrows can form many different kinds of shapes – but pipe cleaners can do even more.  Serrin shaped and attached a 1D shiny pipe cleaner on Maria’s right eyebrow for comparison. We can be playful even as grown-ups, but there is also a serious purpose here. People of all ages are very good at recognizing features of human faces and bodies. So any time you can use your own body to make a math point, do so. And physically laying one shape over another is the most immediate, hands-on, embodied way to compare curves, angles, sizes, and other math or art elements.

Meanwhile, Amy created an even bigger paper loop out of the same standard piece of printer paper. Amy’s science teacher said if you made cuts fine enough, you could wrap your loop around the Earth. Can you imagine doing really, really, really fine cuts to wrap loops around the house or the Earth? Half the kids said they could and half said they could not, pointing out all the problems (slippery roof, the paper will tear, etc.) Kids who point out practical problems have good engineering minds. You can invite them into the human-made world of abstract math only if you specify it’s unreal – it’s all about fantasy and imagination!

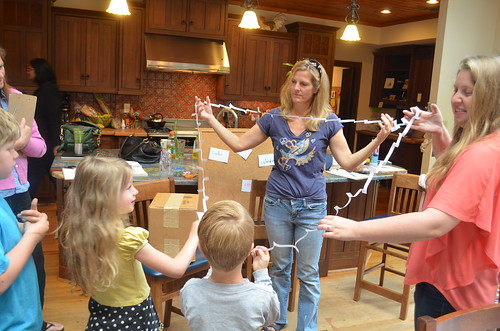
Our whole group was able to fit into the paper circle!

Discussing paper craft techniques.

Everyone gathered around the computer to watch string spin toy (on a flat, 2D screen we might add – but it fakes 3D views). http://www.zefrank.com/string_spinv2/

More math faces: Charles is totally engaged, observing and smiling.

Hanna is trying the String Spin Toy with Maria.

Owen enjoys predicting what will happen next… You ask children to predict things – but don’t judge predictions! Let them experiment and see for themselves.

Boys are happily anticipating how their conjecture would come out.

More portraits of math focus and math excitement.

It’s a spaceship! It’s a castle! It’s a cannon! It’s a viking boat cross-section! Wait, what?

Check out parents thinking and anticipating together with their children.

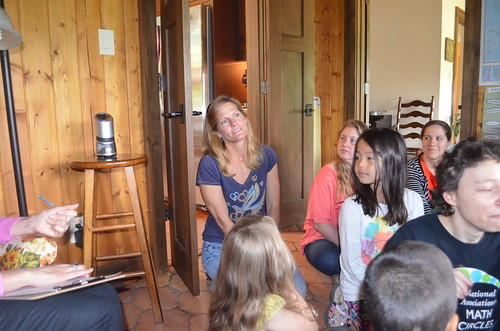
A sketch of the swing we discussed last time. What shape does this triangle make when you rotate it? What shape do you need to rotate to make a cylinder?

The strings are 1D, the shapes we see seem 3D, but we are really watching everything on a 2D screen. Pet the picture on the screen to feel it for yourself!

Each hair is a 1D line, but together all the hairs are integrated into a 3D waterfall (or a cone-like shape). Maya values engineering precision: “But really, each hair is a 3D cylinder.”

We did a bit more of scavenger hunting for shapes out of shapes in many dimensions. The ceiling is made out of planks; can you imagine them infintely thin, like 1D instead of 2D?

And this colorful creation approximates a curve with (straight) bottoms of triangles, for a colorful sun. The semi-random colors and angles of the triangles make the sun look artistic.

Photos by Erin Song, captions by Erin Song and Maria Droujkova, Math Spark by Kalid Azad, Shelley Nash, and Maria Droujkova.