This is the story of the fourth meeting of Sunday Natural Math Circle doing activities inspired by calculus. We started by reviewing some past “book art” style objects that transformed between 2D and 3D, like the spaceship…

…And the spherical paper decoration Eli opened.

Moving on to the next experiment: approximating circles. Start with a piece of plain rectangular paper (in your favorite color of course).

Fold it in half twice: along the length and along the width.

Mark the corner that’s in the center of the paper.

Fold the sides adjacent to that corner to one another, making a triangle.

Fold through that corner again, making a smaller triangle. It’s hard to fold that many layers!

Now for cutting: Maria and Chris are helping Mark by holding his paper still. What shape will we get?

Parents are doing the activity for themselves!

Something funny happens if you fold through a corner that isn’t the center of your paper.

The results approximate circles. Eli’s approximate circle transforms into a nice hat.

Cut it again into a smaller shape. What shape do we get when we unfold it? Is it the same shape (an approximate circle)?

Here comes the challenge – a different way to approximate circles. Use these small circles as a template to build LEGO circles on top of them. Maria: “You figure it out as you go along!”

Our other group tried to build LEGO circles, but they mostly stopped at squares and diamonds and called that “good enough approximations.” We thought that moving off the big LEGO board and onto paper can nudge children into thinking outside of the box. Or outside of the grid, as the case may be.

It worked! Whether the circle was covered in a random way (above) or in a systematic way (below), the LEGO pieces aren’t on the grid anymore.

Parents’ math faces, contemplating:

Maria’s LEGO circle:

Next, Maria shared a way of building circles out of parallel strips. It’s an important method that did not come up among the children. In a larger group it might have – or, if we used craft sticks instead of LEGO blocks. Something to try next time.

Maria and Mark are drawing lines using a plank built out of LEGO as their ruler:

The result is that the circle is split into parallel stripes:

Eli: “Oh yes!”

The letter O started as an approximation of a circle, then grew into a phrase. Eli would show this sign whenever somebody made progress or finished a project. A great way to cheer for your colleagues!

Maria cut the circle into stripes and gave one to each person. For each stripe, people built a LEGO plank.

Then we put all our planks together – integrating a circle.

Oh yes!

Children said our LEGO circle would be so much better if only we could make it really big (or the blocks really tiny… but that’s harder). When asked, they all wanted to try and make a really big circle. To do so, we taped four papers together.

How could we draw a circle?  By folding it like we did earlier, or simply by drawing? (Nice try drawing, Eli!)

Find the center and draw a dot.

Fold one more time.

Cut! We got a triangle.

It’s like a cone… for blueberry ice cream.

Back to the integration:

We started to fill the big circle with planks as before, but that turned out to be a lot of work.

So we filled the middle with the big square block:

Serious team building:

Checking the LEGO circle from the bird’s eye view:

What do you notice about that big circle? A triangle? Any patterns?

Children attempted to find patterns in colors of blocks around the circle, but that turned out to be random. Then Eli alternated between two neighboring single-color planks, naming the colors: green-blue-green-blue-green-blue… Everybody laughed.

Snack time. Slicing and reassembling apples and bananas (shapes out of shapes):

Guess what shape the cuts will be when we look at them from the side. There are problems like that in drafting and 3D modeling.

When I slice this banana what will we see?  Once we slice it, can we straighten it?

One way to straighten: with wedge-shaped gaps on one side.

Another way to straighten: turning every other piece 180 degrees:

A cabbage is an excellent example of a shell integration. It was interesting to just take it apart and then put it back together. Everybody got a wedge to try doing that.

Look around: shapes out of shapes (integration) is everywhere – blinds, light fixtures, woven fabric…

Photos by Erin Song, captions by Erin Song and Maria Droujkova, Math Spark by Kalid Azad, Shelley Nash, and Maria Droujkova, edited by Ray Droujkov.

This is a story about the fifth and final meeting of the Fridays session of our spring math circle. At the previous meetings, children claimed you can’t divide by zero, and Maria promised to show them how next time.

“Wave at me if you have divided by zero!” – several parents did. Then, “Children, wave at me if you believe it’s possible to divide by zero” – some do, some don’t. Hannah: “I believe my mom!” Maria: “And now wave if you think dividing by zero is a bad idea.” Offer people funny or interesting multiple choices, so however they “vote” they feel good about their chosen option.

Maria asked 3 children to come forward to be her “math magic” apprentices. But if they aren’t into magic, just calculus apprentices. Maria and Amy are helping them with apprentice capes. Usually we pretend-play without prompts, but we wanted to play this up a bit.

Maria the magician and her three apprentices are warming up for math magic.

First, grab 6 pieces of paper. Let’s think: how many groups of 2 do you have?  6:2 = 3. Children demonstrated, each with 3 stack of papers with 2 pieces in each.

Then we modeled 6:3 (2 stacks of paper with 3 pieces in each) and finally 6:6 (just 1 stack). Note that adding 0, dividing by 1, dividing the number by itself, and other “border cases” should not come as your first example.

Then we modeled the same question about parts (fractions). How many halves are in three pieces of paper? Six. Take one large piece of paper. How many halves are in it? Two.

And then we started a series of division, modeled by folding the large piece of paper. When you describe it in words, it’s messy, but imagine words only following the play. Words were only in the background of paper-folding. Even the youngest in the group loved folding their papers again and again.

• How many halves are in it? 2. Dividing 1 by 1/2 gives you 2.
• (Fold again). Now you get 4 parts. That’s because dividing 1 by 1/4 gives 4.
• (Fold again). Now you get… How many parts? (Some thought 5, because it’s the next number after 4, some 6, because we had 2 and 4 before and they skip-counted, and some thought 8.) Count! You get 8 parts. That’s because dividing 1 by 1/8 gives 8.
•  (Fold again…)

Priyesh:  “After 64, you can’t fold the paper anymore; it’s impossible!” Priyesh was squishing the folded paper tight to demonstrate.

Charlie’s trying to make that last fold happen by using his teeth.

Charlie: “Ah-ha!  I did it!”

After the fold, Hannah and Michele are counting the squares together.

Hannah is tracing the fold lines, while Serrin is numbering parts on her paper.

Small circle time.  The apprentices are sitting next to each other. Maya joined Priyesh under the same cape, and Serrin is rescuing Maya from the bright sun.

Math faces: children are following along the story of paper-folding and fractions they’ve just experienced for themselves.

As we fold: 1, 2, 4, 8 pieces… Each 1, 1/2, 1/4, 1/8 as large as the whole paper…

Serrin the apprentice represented the number of pieces (1, 2, 4, 8…) and Hannah represented the size of each piece (1, 1/2, 1/4, 1/8…) As Hannah got down to show pieces getting smaller and smaller, Michele lifted Serrin to show the number of pieces getting larger and larger… “To infinity and beyond” as the saying goes.

“Anthropomorphic personification” is the fancy term for pretend-playing your mathematics with your own body. As you can see, children enjoy it very much. This is also one of the best ways to learn and to remember. Our minds have very powerful mechanisms for dealing with people and relationships.

One enthusiastic and dedicated mom needs to catch her breath after all the heavy lifting! What wouldn’t  she do to help children learn?

Maria also used her hands to show the ratios and relationships between the size of the fraction you divide by (smaller and smaller) and the result of the division (larger and larger). Note how many ways we used to explore the same thing: paper-folding, heights of children, the distance between hands, words, and written symbols. Three to five different ways work well for new topics. As you explore your topic in depth, create more and more representations!

Next, Maya and Priyesh represented the numerators and denominators of our changing fractions, since they were together under the same cape. A fraction is one number, but it comes in two parts.

Maria is talking with Julianne after the fraction activity. Julianne is telling her own story of the experience.

(Mad-Mathematician-Magician) Maria made division by zero madly magical – with much help from the apprentices!

So what do you get when you divide by zero? Children made up their own hand or whole-body symbols for infinity. You can see three or four different versions. Creating symbols is a big part of mathematics. There are usually several different ones, for example, / and : for division.

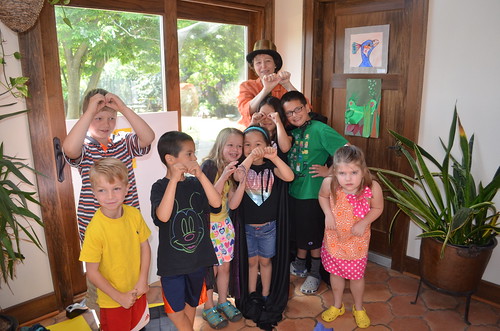
Silly faces and infinity!

Back to the table …

Maria helping Maya with her project: making curves and 3D structures out of fan-folded paper.

Maria is about to represent derivatives (slices) and differentiation (taking apart) by cutting an apple.

Apple cut in half horizontally in the middle; “What shape would you see? Circle? Cylinder in 2D or 3D? Or an approximate (calculus) circle?

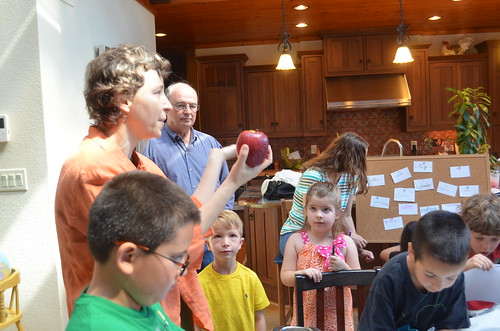
Also, what shape will that center piece of the cutter make? “A cylinder!” – say all children. Then one voice corrects, “Two halves of the cylinder” – someone remembered the apple is already sliced in half.

Modeling a cylinder out of paper while we are at it!

And after we slice (derive), we can assemble (integrate) back again.

Younger children – Owen, Julienne, Eashan, and Jake – are focusing on the “integration” of the apple. Parents sometimes worry that, to quote a favorite movie, “You keep using that word. I don’t think it means what you think it means!” – that we or the children stretch the meanings of math terms too far, or apply words inappropriately. Owen told Amy he needs to integrate his sock drawer, whatever that means.

But words end up meaning something to children. Five-year-olds have no need for high precision: they are not landing spaceships on Mars or building reliable bridges. They are just exposed to ideas. As a parent said recently about her early math games with her mom, “I don’t remember ever not understanding about negative or complex numbers.” We do want that feeling of happy familiarity. The precision and depth of understanding will grow with time.

Eashan is modeling the slicer in 2D. Check out the accuracy: there is a circle in the middle and the same number of sections.

Moving onto the next activity.  A thread from a yarn is 1D (well, a model of a 1D object – like everything else in the physical world, it’s really a 3D thing).

Meanwhile, Charlie is determined to fold the most squares possible. Children sometimes continue their projects while the group moves on.

The final result:  Ta-da!  390 squares! Maria: “That would be an interesting power of 2. But he used different folds.”

Pom-poms embody the idea of integration. Wrap the yarn at least 30 times around your hand (making a 2D surface out of 1D lines). Then tie it across the lines, cut the lines on the opposite side from the tie, and fluff up into a 3D shape.

Integrate into a toupee?

Children are creative: how about a mustache for Hannah?

The Flying Spaghetti Monster lands on Serrin’s head.

How charming, mustache ladies!

Evil Mustache Priyesh is threatening the Flying Spaghetti Monster.

Meanwhile, Eashan is still at it integrating/deriving in 2D.

Julienne is making a 3D bird’s nest. She is very much into nature and modeling natural objects. Children often go through periods where everything must be about a single topic: horses, Star Wars, the nature, and so on.

Check out Owen’s 3D mustache…

…And Jake’s 1D looong beard!

…And Charlie’s fancy, mostly flat beard and fluffy toupee.

Our final collection of Math Words. Some are made in multiple colors because several children wanted to add the same word. Each child selected a color and wrote a part of that word. “Make math your own!”

Lastly, the group is gathered to watch the trailer of “Flatland.”

After the video, the grown-ups stayed around for some math talk, while children played outside.

Photos by Erin Song, captions by Erin Song and Maria Droujkova, Math Spark by Kalid Azad, Shelley Nash, and Maria Droujkova, edited by Ray Droujkov.

This is a story about the third meeting of a Calculus for Kids math circle. During these meetings, we offer children and their parents prompts, but then follow their ideas to new places. This way, children help us design!

Maria has returned from her trip to the Navajo Nation, and brought this vase. It is decorated with symbolic patterns that remind us of one of our math words: Integration. Maria asked a question about what this symbol might mean, so Allison is examining the vase to search for her own meaning.

Sometimes children fall into a curious trap; they realize they can give universal answers to many different questions. This is an excellent math principle for children to discover and should be celebrated. For example, on a scavenger hunt for hidden math, children say any object whatsoever has “a pattern” in it. Celebrate by confirming patterns are everywhere and that it’s clever to notice that. If you are looking at shapes in figures of revolution (our previous meeting), instead of seeking cylinders, castles, or flowers, children can say, “Alien spaceship” and it will probably apply to any shape. Again, celebrate children’s ingenuity by saying that alien spaceships come in all sorts of shapes – it’s just like mathematicians saying, “Shape” to mean a large category of objects.

When children overdo this, the activity becomes boring and needs to be rescued. One way to pull children out is to ask for details. What sort of spaceship? What pattern do you see? Here, Maria is leaning forward asking to hear and see Eli’s interpretation of the symbolic pattern circumventing the vase.

Let’s integrate a 3D paper spaceship out of 2D parts.  Maria drew an outline of a simple rocket ship to show what we are about to create.

First, take four sheets of paper, fold them in half, and draw only a half of a rocket with the center line along the fold line. This is a nicely challenging task. Why do you draw a half? What happens if you draw the whole ship? What if you draw along the other side, not the fold line? Allison is holding the paper down so Sydney can draw easier.

Maria’s showing her rocket drawing as an example.

Then, cut along the outline of the rocket, as Eli is doing.

Maria is holding and turning the paper so Sydney can maneuver the scissors better. These types of assists help children do more with physical objects. Why do we care? Why not just cut for the younger child? Because the connection between the hand and the brain is two-way. By handling paper, children directly teach their brain about shapes and their mathematical properties. In this case, about the slope.

Next, open up the rockets and staple along the fold line. Krishnan is stapling the rocket they are making with Yash.

Once it’s securely stapled, spread the layers of paper around. This models disk integration for bodies of revolution.

Image from Wikipedia.

Spaceships look realistic enough for the shape, but do they really fly, children ask? They try, and it turns out that no, these models are just for looks.

So the group is back to the table, where Maria is about to teach them how to make a 3D paper airplanes that really fly. This is an example of how children help to redesign activities, if we only follow their actions. We did not plan to research which models fly well (and why). But, it’s a rich question that made our activities livelier.

Maria talked through every step. A lot of asides about math terms come up when you do. Here the steps are all in one place, because it’s easier to understand this way if you are reading rather than playing along with someone:

First, fold a sheet of paper in half vertically.

Then fold the top right and left halves along the middle line, forming a triangle.

Observe how children think and do things differently. One triangle is facing upward and the other downward. Which is correct? Even with simple technical tasks, there are many right ways of doing them.

Next, fold the whole triangle down – or up, if you are holding your paper the other way!

By the way, children tested their planes after each and every step! Eli tried it first as a joke when we first folded the paper in two. Maria kept up the joke and said that this “airplane” does not even fall well. Everybody wanted to try, and then they kept trying with all the intermediate steps.

Some modeling techniques create models that get progressively better with each step. Riemann sums (above, from Wikipedia) are this way: the smaller the intervals, the better your approximation, but at each step, the approximation does work. Other modeling techniques are not progressive, and you have to wait till the very end to see any result at all. Children were experiencing that second kind of modeling with paper airplanes. They had a lot of fun with the unfinished models flying so badly that they didn’t even fall well.

Progressive techniques are used in many fields. For example, web design and image coding.

Now, fold in a stabilizer: a tiny triangular tip of the larger triangle. This way, the plane won’t wobble, but have a nice balanced flight.

Again, fold it in half symmetrically: here come the wings!

Maria is helping to fold. The next step is tricky.

Yash is about to test-fly his handmade 3D paper airplane. Sydney is still working on decorations for her spaceship. Sometimes children stay with a project longer, but they still observe others – especially their parents – doing the next one.

Maria and Sydney are flying Maria’s paper airplane back and forth and Yash keeps testing his with Krishnan.

A trick to make the planes fly better: straighten the wings really nicely.

Sydney is ready to test-fly 2 airplanes at the same time, while Maria is watching the circle flying their planes from a cozy cushion.

Sometimes things do not go the way we planned or designed – there was an airplane accident! Accidents happen even in math circles. Leaders need to be prepared to deal with sad or upset children.

The circle is about to move onto the next calculus activity: making spaceships another way.  Maria is handing out packaging foam to model layers.

Ah, so soft. Sydney and Yash also assembled spaceships out of LEGO blocks.

Let’s look at the 3D paper rocket ship from the side, but integrate them from horizontal slices. From the side, the top looks like a triangle, the body like a rectangle, and the thrusters like a trapezoid.

We did not want to slice our models to see how they would look across. But Maria had fruits there. She chopped a pear horizontally (like a Fruit Ninja) and asked, “What will you see when I show you the cut?” Some children answer questions about fruit slices in 3D (a cone, a cylinder), and some in 2D, from different points of view: the side (a triangle) and the top (a circle). This is a good example of how many right answers there are for one simple question!

Maria sliced the pear horizontally, then numbered each of the four slices. Except nobody wanted numbers 2 and 3, but two people wanted number 4. We ended up creating our own number system: #1 – Sydney, #infinity – Yash, and #4A and #4B for the two boys who both liked 4.

We had a brief side discussion about naming numbers every which way – how about “cow” as a number name? Children concluded that these funky number names are more like variables than numbers.

Then children traced their fruit slices onto paper plates, cut them out, traced on the green foam, and cut out foam circles. Snacking on fruit all the way! Food makes people happy. Check out Maria’s face – yep, like a happy fruit ninja. Food makes for smoother, friendlier math circles.

The nosecone is finally integrated out of the four circles.

And later, when participants made more circles, we could integrate the whole spaceship.

Why do we care? Simpler shapes (like disks) are easier to measure, so we can build more complex shapes (like cones) out of them and measure these more complex shapes too. For example, you can approximate the volumes of cones, spheres, and parabolic antennas by slicing them into disks.

Maria:  If I cut this pear vertically what do I get?

Eli:  A rocket ship!

Maria: What shapes would I get when I cut this orange?

What’s the math name of the orange quarter 3D solid?

Ninja chopping continues…

Group photo-op with our 3D rockets!

Photos by Erin Song, captions by Erin Song and Maria Droujkova, Math Spark by Kalid Azad, Shelley Nash, and Maria Droujkova, edited by Ray Droujkov.