This week, we created the same object in several different ways. The goal was still to make shapes out of shapes, but this time, we compared and contrasted different ways of doing so. Do we place pieces at random like a pile of rocks making a cone, or do we tessellate them in a careful pattern? Do we use small pieces, large pieces, or vary the sizes? Do we use a continuous (pliable) medium like clay, or discrete pieces like LEGO blocks?

Here is this week’s Spark in PDF. This will help you get started on activities.

Serrin is making a braid out of 3 pipe cleaners. She already made one, and off-camera she’ll make a third braid, because…

…This way she can make a braid out of braids. It takes 3 pipe cleaners to make a braid, and three braids to make a braid out of braids, which makes 3^2 (three to the power of two) or 9 pipe cleaners. You can see this braid out of braids between 3 LEGO blocks and a cube of 3^3 (three to the power of three) LEGO blocks we made with Maya and Serrin earlier. The braid of braids fits there, because the power of two represents 2D, while the cube represents 3D and 3 single pink blocks represent 1D (especially if you line them up).

Nobody was eager to suggest a shape for everyone to build, so Maria suggested a snail, because it appeared in several crafts before and was a simple enough but interesting shape. Let’s start with 1D medium, the pipe cleaners.

Her own project done, Serrin started using pipe cleaners and other media to make snails.

Here a single LEGO block on top of 4 blocks represent an approximation of a 3D shell. The 2D pink sticky note on the bottom stands for the body. We talked on how math is similar to impressionist or abstract art, and this is an excellent example.

Hannah is testing and bending a 1D pipe cleaner while Owen is imagining how to make a snail from a multitude of them. He started with a tiny multi-colored ovoid, about half as long as his thumb, then the project grew.

Hannah made a 2D tiny green snail from yarn stapled together. Hard to see, but very soft and cuddly!

Hannah made another snail; a 3D purple sphere yarn ball topped with a 1D curved orange pipe cleaner for the snail’s antenna. Check out Hannah’s triumphant and crafty smile. That’s a math face for when you find a simple solution to a complex problem. Simplicity is a big mathematical value, and solving problems in simplest ways possible is considered a beautiful thing. “Everything should be made as simple as possible, but not simpler” – Einstein, paraphrased by the composer Sessions (because music shares this simplicity value with math).

Owen sitting quietly alone working on his snail. When transitioning between activities, leave some time for kids to get to a place where they can pause their projects gracefully and hold their thoughts.

Ecstatic smile, Priyesh! Maya and Priyesh are discussing their LEGO snail projects and just chatting. Priyesh focused on shape, making his snail sturdy and “more three-dimensional” as he put it, and Maya focused on the pattern of colors, analyzing the layers.

Julianne wished she had a real snail to draw it just the way real snails are. Maria helped in a different way: offering shapes that Julianne could choose for parts. Then Julianne integrated the snail out of parts, choosing which to draw next, which shape it will be, and which size of that shape. This “calculus way to draw” (making shapes out of simpler shapes) helps kids who want to be precise – another value some forms of art share with mathematics!

Michele integrated her (2D) snail using pink sticky notes, dramatic on black construction paper. Check out how curves are made of rectangles.

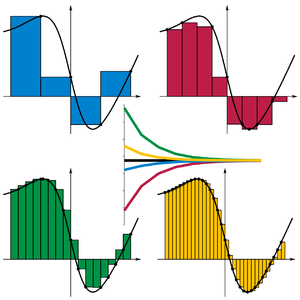
Image credit: Wikipedia article on Riemann sums.

The grand imaginary play battle – Snail vs. Snail, now in 3D! Maya and Priyesh were at it for a while, building their snails up and then pretend-battling them. Making your own pretend-worlds is what children – and mathematicians! – love to do.

Image credit: Wikipedia article on the made-up world of imaginary (complex) numbers. The picture looks like a battle of rainbow snails, but it’s a graph of sin(1/z).

This time, we had different rules for our Math Words: people got to pin the word if they did not know it yet. Children are generally okay saying they don’t know something, and this game celebrates awareness of not-knowing, then learning.

“Wave at me if you made a snail using only 1 color! Now, if you used more than 1 color to “integrate” or put together?” Many kids wanted to write the word integrate, so each wrote a letter in a different color, integrating the word itself out of  letters. Here Serrin and Hannah are about to put up “Approximation” and Owen, “Abstract.”

We had a cute little scene about abstraction. Maria asked for people to wave if they made a model somewhat resembling a real snail. Then to wave if their model was pretty far from real snails. “Mine was nothing like a real snail, AT ALL!” – very happily explained a kid, and several others nodded. Then all children started to wave. This is a happy attitude to keep, for both math and art. A formula for a parabola does not resemble the ball flying out of your hands… The formula is abstract, like a model of a snail that does not look like a snail at all.

We are sitting on the ground: “What would make our approximations more perfect?”  The participants had ideas for making shapes more precise, but also for artistic merit: “Find enough LEGO of only one color; use smaller pieces or make a larger project; use a better pattern; observe real snails!” Julianne made a passionate speech about following the nature and not messing with it too much.

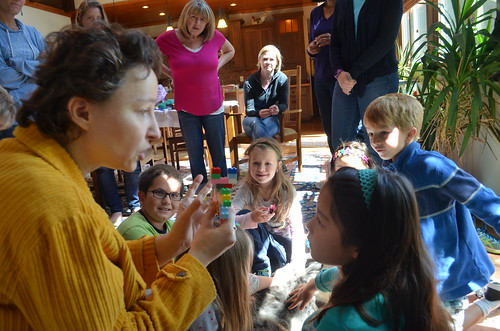
Owen: “My snail could have used a pattern…” Maria: “Look at all the randomness!”

We have a new videographer! Thank you. Videos coming up.

Maria and Jewell are discussing Julianne’s stories that Jewell was recording.

We are integrating a spiral snail out of our own hands. Try to work out your math with your own body – it makes for a very direct understanding, like nothing else does.

The sun made a piece of impressionist art out of our snail.

Making people pizza with our legs. It’s a… math circle! A child: “We are not pizza slices, we are lines between the slices.”

All the Math Words.

Video time: Watching “Infinity Elephants” by a mathemusician Vi Hart.

It’s nice to finish with a movie, because it takes less energy from the tired kids, but leaves them focused, calmer, and inspired for their trip home.

Photos by Erin Song, captions by Erin Song and Maria Droujkova, Math Spark by Kalid Azad, Shelley Nash, and Maria Droujkova.

This week was all about Flatland. Download the Math Spark that invites you to travel to Flatland with us.

Before new activities, we sat and reflected on what math we had noticed last week. Check out what we call “mathematical faces” – when children think about mathematics, their faces look special.

“Sometimes, these thoughts can make me gigglish!”

Maria is taking the tools (papers, sticky notes…) out for the hands-on creative activities on the table. Do your children have trouble transitioning into activities? Make it a ritual to set the table for mathematics with colorful materials, and whatever you need to feel good – snacks, drinks, and toys. Rituals like this give children time and a framework for transitions.

Maria:  “Look at this 2D hairband.  It is curved but also can be straightened out.”  We can manipulate some 2D surfaces to be either flat or curved.

Priyesh cut out a 2D shape (bound by curves) for his football project.

Maya is in the process of making and playing a 2D orchestra – two drums so far, a circle and a square.

Maria is listening to the story of Owen’s project: his (2D) coffee filter represents a (3D) ice block with cuts representing cracks. We use black or bright construction paper for dramatic backgrounds to models. It helps with storytelling.

Maria is about to show how to make a shape similar to Owen’s with just one cut of a (folded) coffee filter.

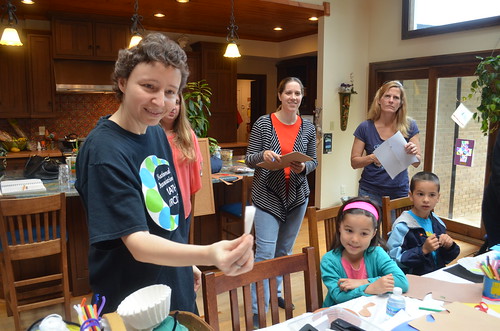
“What do we have here?”

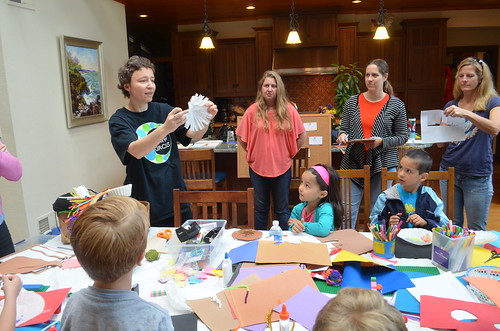
Another example of how a 2D flat paper can turn into a model of a 3D spiral snake.

Charles is making a random 2D decoration for his wall, with each piece uniquely, irregularly shaped. Another math or art term for random shapes is “abstract.”

For his next project, Charles triangulated a turtle-bobcat, then added dots for more regularity. This is similar to a technique from Australian Aborigines.

Lori constructed a curved shape (a circle) arranging LEGO blocks that are straight squares. Then she commented how the shape becomes smoother and the triangular wedges between the squares become smaller when you use more blocks. You get a more precise approximation of your circle with a polygon that has many, many sides.

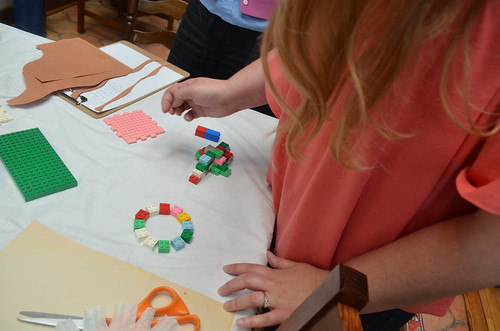
Can you cut a hole in a piece of paper that is large enough for you to fit through? Amy shared a way… Besides, you can use the resulting zigzag to form curves, like a big goofy smile or a circle.

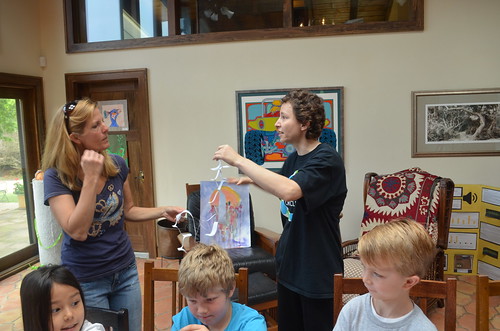
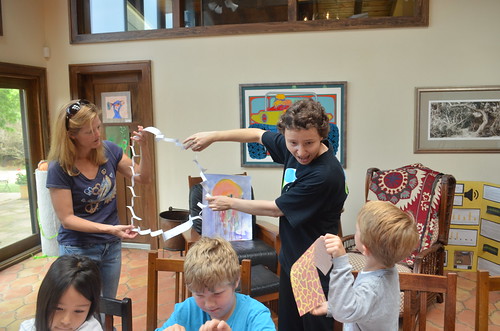
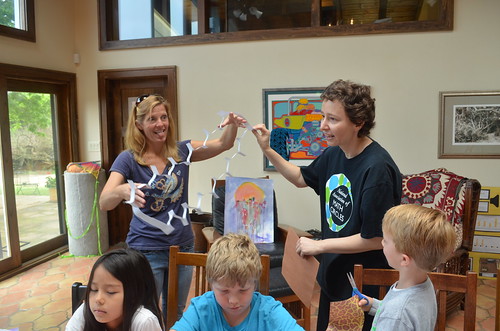
Now that the 2D ring is cut out and formed, let’s see if we can go inside the ring!  First comes Serrin.

Then, Eashan…

…Finally, Maria sneaks in for a photo-op.

Eashan is busy making a mosaic of a waterfall (2D, curved) out of sticky notes (also 2D, but straight).

Maria is showing a 2D face Serrin made with 1D details out of pipe cleaners (very curved).

“Can your eyebrows curve like this?!”

Our eyebrows can form many different kinds of shapes – but pipe cleaners can do even more.  Serrin shaped and attached a 1D shiny pipe cleaner on Maria’s right eyebrow for comparison. We can be playful even as grown-ups, but there is also a serious purpose here. People of all ages are very good at recognizing features of human faces and bodies. So any time you can use your own body to make a math point, do so. And physically laying one shape over another is the most immediate, hands-on, embodied way to compare curves, angles, sizes, and other math or art elements.

Meanwhile, Amy created an even bigger paper loop out of the same standard piece of printer paper. Amy’s science teacher said if you made cuts fine enough, you could wrap your loop around the Earth. Can you imagine doing really, really, really fine cuts to wrap loops around the house or the Earth? Half the kids said they could and half said they could not, pointing out all the problems (slippery roof, the paper will tear, etc.) Kids who point out practical problems have good engineering minds. You can invite them into the human-made world of abstract math only if you specify it’s unreal – it’s all about fantasy and imagination!

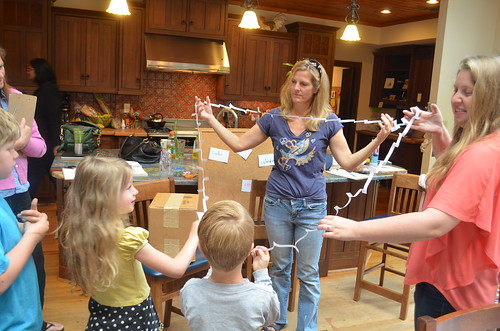
Our whole group was able to fit into the paper circle!

Discussing paper craft techniques.

Everyone gathered around the computer to watch string spin toy (on a flat, 2D screen we might add – but it fakes 3D views). http://www.zefrank.com/string_spinv2/

More math faces: Charles is totally engaged, observing and smiling.

Hanna is trying the String Spin Toy with Maria.

Owen enjoys predicting what will happen next… You ask children to predict things – but don’t judge predictions! Let them experiment and see for themselves.

Boys are happily anticipating how their conjecture would come out.

More portraits of math focus and math excitement.

It’s a spaceship! It’s a castle! It’s a cannon! It’s a viking boat cross-section! Wait, what?

Check out parents thinking and anticipating together with their children.

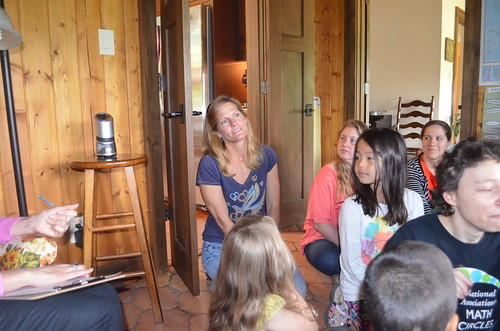
A sketch of the swing we discussed last time. What shape does this triangle make when you rotate it? What shape do you need to rotate to make a cylinder?

The strings are 1D, the shapes we see seem 3D, but we are really watching everything on a 2D screen. Pet the picture on the screen to feel it for yourself!

Each hair is a 1D line, but together all the hairs are integrated into a 3D waterfall (or a cone-like shape). Maya values engineering precision: “But really, each hair is a 3D cylinder.”

We did a bit more of scavenger hunting for shapes out of shapes in many dimensions. The ceiling is made out of planks; can you imagine them infintely thin, like 1D instead of 2D?

And this colorful creation approximates a curve with (straight) bottoms of triangles, for a colorful sun. The semi-random colors and angles of the triangles make the sun look artistic.

Photos by Erin Song, captions by Erin Song and Maria Droujkova, Math Spark by Kalid Azad, Shelley Nash, and Maria Droujkova.

This is a photo gallery for a math circle called Calculus for Kids, in Cary, NC. Math circles are informal groups where children, their families, and teachers explore math together. This session was our first introduction to making shapes out of shapes. Here are two pieces of supporting materials for the topic:

One-page Math Spark for building models.

One-page sheet with relevant terms

Emma is drawing on (2D) paper and also creating a 3D model out of pipe cleaners, inspired by a 3-dimensional dolphin.

A fictional narrative:  “A jellyfish taking a ride on a dolphin.” Check out the evolution of the pipe cleaner model from the photo above.

Maddie is using (1D) pipe cleaners to create a wide, 3D ice cream cone.

Mark is inspired by Wall-E and fractals. He brought a 3D printed fractal to share.

Inside the fractals, there are squares, lines, empty spaces…

Sydney is adapting a story of Frozen recognizing the symmetry of sun.

The song “Let It Go” from “Frozen” popularized fractals:

One of the main characters Elsa is skating; the whole composition is also symmetrical. 3D Elsa is similar to the 2D version.

A 2D balloon with circular patterns made from playdough.

Eli is miming one of the things he likes. Maria’s not getting it.

Eli finally his wish (without breaking it) by writing. Children need to have multiple modes of expression so they can choose, and we must respect their choices.

Maggie and mom Rebecca are gathering 1D pipe cleaners to build a 3D spiral bird’s nest.

“Eggs are growing in the nest…”

And the (potentially) endless spiral reminds us of infinity.

Yash is creating a laser torch project – finding squares, circles, and cylinders in LEGO blocks.

“I built a birthday cake, a sky scrapper with two elevators, and some stairs!”

The stairs represented the counting sequence going up and also down (5, 4, 3, 2, 1). Later, another example of a sequence – 2, 4, 8…  – was built as well.

Julie made a 2D spiral glasses using 1D pipe cleaners.

Allison made a ring consisting of a small sphere and a large circle.

How can we make numbers out of ourselves? Each of us is 1 (The One?) – then parent+kid makes 2, or we can use fingers, arms, legs, point out the eyes…

Again, things develop and grow (a bunny ear out of Mark’s head). And number 3 is formed by 3 boys standing in a row.

Could we try making a spiral with all of our hands together?

Let’s make a human square on the body pillows… hmm,  1, 2, 3… seems like we are missing something… we need one more person to make 4 sides!

We need to hold our arms and legs as straight as possible; a square has 4 sides, 4 angles attached to each other, like this.

A cylinder please!  Imagine 2 circles and a folded rectangle between, holding us on all sides, as we extend our arms circularly and spread our feet.

Now, this 3D shape tapers nicely from a flat base to a point, the apex there our feet stand together; a cone upside down!

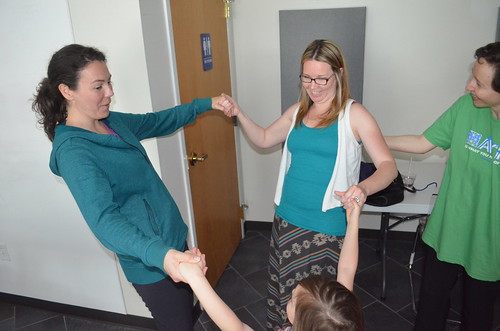
Julie and Allison are making a human pentagon; raising one side of their arms (2 sides) attached by the tips of their fingers, bodies (2 sides) and the ground as the last side.

Yash and Mark are making a 2D roof top by attaching their hands and bodies facing each other. The surface is supplied by the imagination.

Maria:  “Grown ups, try this! Feels sooo good.”

Yeah!  Jumping on two over-sized cushiony square pillowy mats: so relaxing and comfy!

What have we here on the ceiling? Lots of patterns, as children suddenly point out!

We discovered these hidden math words from our own imaginary creations (hands-on-craft) during the one hour of our math circle. For now, most words are shapes. Let’s see what words appear by the fifth meeting!

Photos by Erin Song, captions by Erin Song and Maria Droujkova, Math Spark by Kalid Azad, Shelley Nash, and Maria Droujkova.

This is a photo gallery for a math circle called Calculus for Kids, in Cary, NC. Math circles are informal groups where children, their families, and teachers explore math together. This session was our first introduction to making shapes out of shapes. Here are two pieces of supporting materials for the topic:

One-page Math Spark for building models.

One-page sheet with relevant terms

Calculus for Math Circle begins!

Ice breaking time:  Who are you? If you’re happy and you know it raise your hand… We take turns naming one thing we love, and whoever else loves it too – waves.

Bonk on the head to show whose turn it is to introduce themselves.

If Maria bonks everybody on the head, who bonks Maria on the head? All together now…

Julianne loves to draw.

Maya wants to make a 2-dimensional fan!

I want to make a pine cone in 3D shape!

An hour later, many different models of the cone:

Serrin making tree-trunk as a 3D cylinder using orange 1-dimensional felt.

Cylinders are popular: here they serve as legs for a future doll:

Let’s make a cylinder out of ourselves. Or is it a circle? It’s both, kids say: depending on how you look at it.

What kind of shape is this?  Triangle? Half-circle?

Maria pointing shapes she found in the backyard

How do we make a square?  Team building time. A square has 4 sides and 4 angles … “Let’s see, how many people do we have here? 1, 2,  … 8.  Okay, so a square has 4 sides if we divide by four that’s two people for each side.”

The group square is finally made! Smile!

We found another shape!  The table is made out of 2-dimensional glass circle! But it’s also a 3D cylinder, children say.

Here are the list of math words we collected from our creative craft makings on the board. Let’s see how the list growth from meeting to meeting.

A snail and a 3-dimensional diamond shape Lego block.

Making 3-dimensional pine cone with 1-dimensional pipe cleaners can’t possibly be this fun, right?