From buttons to the multiplication blind spots

Buttons as a a tangible representation of a set
My kids love playing with our button collection. Who does not? Buttons are colorful, cute, interesting objects. They are also an incredibly useful mathematical manipulative – a tangible representation of a set. Today we have decided to arrange 1, 2, 3, … , 34, 35, 36 buttons into groups. The first task was to divide the 36 buttons among three siblings.

36 is 3 times 12
Without the use of the multiplication table, sharing buttons is a game in its own right: “One for me, one for you, one for our toddler sister.” “I hate pink buttons. Let’s trade.” Surprisingly enough, every single one of them ended up with the exactly the same amount of buttons. So we went on to the next challenge. Can you guess what it was just from looking at the picture?

A new arrangement
One day we will arrange the buttons in a square and add the connection to 6 x 6.
In the good old (hold on, I am undecided on ‘good’, but I am definitely not that old) days, I learned the multiplication table with drills. No visualization, just tons of practice. I can still calculate the answers to mathematical problems in my head, on a piece of paper, or even on a blackboard when I teach. I also love talking to people about education and math teaching, in general. Some believe that today’s kids will live in a world surrounded by technology, thus we should teach them to type, program, and use a calculator as soon as possible. Others are horrified by today’s youth lacking mathematical skills. The rest are busy changing the educational landscape.
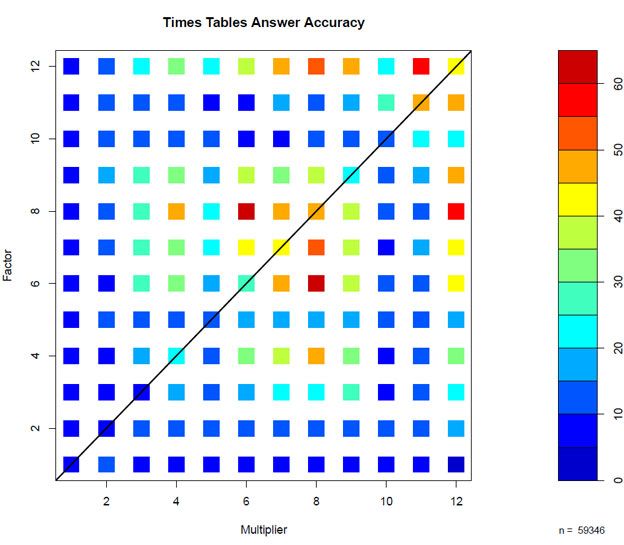
Recently, I have noticed that recalling 7 x 8 = 56 takes me a good deal longer than say, 8 x 3 = 24.
As a very curious person, I took a poll among my friends. Most of them have learned to multiply in a similar manner. :) To my great relief, I am not the only one suffering. Even though the location of the blind spots is individual. So far, I have just colored in the separate responses: 6×9, 7×8, and 8×7 seem to cause most trouble.

Multiplication blind spots
Can you recall all of the facts from the multiplication table equally well or do you suffer from a blind spot? If so, please share its location. I would love to create a more accurate map of multiplication table blind spots, but I need more respondents.
In the meanwhile, check out the Who, What, Why article Why does the sum 7×8 catch people out? about times tables answers accuracy.
Related Posts
Posted in Grow







Hi Maria,
My biggest blindspots are
6×7 and 8×7
:)
Hi Caroline,
thank you for sharing. Irina