Do your little kids draw grids?
What do you see when you look at drawings by little kids?
For example, grown-up artists noticed that many young artists draw big heads with legs. The more people talked about these shapes, the more meaning they found. By now developmental psychologists developed big theories of development around these simple observations: “Tadpole drawings appear during the pre-schematic stage…”

Grown-up mathematicians noticed that many young mathematicians draw grids. Round grids, square grids, grids within grids!
Have you kids made any grids? Please send us pictures and stories!

Here are some masterpieces from Michael Kelly.


Michael writes:
Our youngest son Francis began drawing pattern grids and intersecting lines when he was about 3 years old. He seemed to draw in a way that resembled his early language learning. He didn’t draw discrete objects but would rather make patterns and connections across the whole space. In a similar way, in his speech he did not repeat individual or ‘favourite’ words, but he often copied the cadences of, or flow within, a sentence.
Strapped into his baby seat in the car he once interrupted a stream of jokes and laughter between four adults which he had been silently witnessing. When he had noticed the pattern he gave his own version of a line of ‘speech’ followed by his own appreciative laughter. His timing was great. Everyone stopped… none of us had considered how a 15 month old child might be making sense of the vocal expressions and social conventions of our adult friendships!
Franny’s drawing showed awareness of relationships between local shapes and overall design, and the negative shapes were sometimes integrated too.
We already have a bit of theory on grids and kids. Grids are to individual cells as paragraphs are to words (in Michael’s example), or songs are to notes. The whole grid is bigger than the sum of its parts, and kids think in terms of the whole of the thing! But some children start by drawing individual cells next to one another, like so:

Even older kids and teens may draw individual cells when they work with new grid ideas. Here is another example from Math in Your Feet:
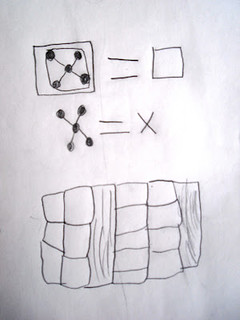
At other times, children make grids by having long lines cross in many places, so the cells multiply:

We have four chapters of grid games in the Moebius Noodles: Adventurous Math for the Playground Crowd book. Check them out!

Related Posts
Posted in Make
2 comments on “Do your little kids draw grids?”
1 Pings/Trackbacks for "Do your little kids draw grids?"
[…] collections, for example, about toddlers and young kids who draw grids, or publish them as separate guest blog posts. Another important contribution is questions, and sometimes we call for thematic questions as well, […]







Hi, I know this post is really old but I was Googling “why does my child love drawing grids” and came across this article. I couldn’t find a single other thing on it. My six year old has been doing grid like drawings for some time, then stopped maybe because of starting school and trying to draw more observational stuff like most other kids tend to (but actually he doesn’t seem to really enjoy that so much) but he’s recently started up with the grids again and I’m blown away by some of them.(happy to share if helpful). He is very mathematical, counting to over 100 before turning 3, and goes through phases of counting in bed into the thousands (which makes me feel uneasy tbh!!). I’m very conscious of the importance of leaving him to it and allowing his mathematical brain to develop as it will but would also welcome any advice on resources to challenge him a bit more which I don’t think he gets at school currently.
Hi,
Glad you found this old story! Yes, I’d love to see your son’s grids – email them to reach.out@naturalmath.com please. Each child’s grids are unique and curious. Having said that, drawing them is more common than most people notice, or realize. Anyone who doodles tends to doodle grids sooner or later. There is even a movement in the arts and crafts community for doodling grids: check out Zentangle, for example.
I hear you about the uneasy feeling. I’d like to assure you that it’s common. A lot of people, even young children, rediscover how soothing certain math activities can be. In school, we often associate math with high-strung feelings. Anxiety or fun challenge: two types of excitement. In fact, math can be serene and peaceful. You can offer your son math activities that support a wide range of feelings. Then, he can choose what to do and when. For serene, meditative feelings try math art, like http://weavesilk.com/ and similar. For a more high-energy experience, try https://www.explodingdots.org/ For a bit of pretend-play, check out https://en.wikipedia.org/wiki/Zoombinis (a classic game with a modern PC and phone app versions also available). There are some great tabletop games like https://mathforlove.com/awg/prime-climb/