Math Teachers at Play Blog Carnival #67
Want to write about playful math for the next carnival? See a blog post you like? Submit your links at Math Teachers at Play!

Deep math
Evens and odds at f(t)
Kate usually works with older kids. Following comments from elementary school teachers, she became “a little obsessed” designing a lesson about proofs for young kids. Making deep concepts accessible is an exciting, challenging quest! The post starts with the video about proofs and creativity: what makes us different from computers. It has several visual, hands-on ideas that can introduce proofs to second or third graders. The activities start from students capturing their “noticings,” forming conjectures in Socratic dialogues, and eventually proving the conjecture that odd+odd=even.
Sasha first saw modeling of deep math with dolls at our place, Moebius Noodles. The first challenge Sasha designed for her daughter Katie was to alternate boy and girl dolls, in a story about a ball. With three of each, and six chairs in a line, Katie succeeded. Can you solve the same problem if one more boy arrives? Can you change the degree of all the vertexes in the graph to two, that is, help every doll to have two neighbors, while still alternating boys and girls? Grown-ups know that to change degrees of vertices, you need to change the shape of the graph, that is, to move the chairs into a new configuration. Can a little kid figure it out? Read on!

Robert is building on factorization diagrams, especially on work of Brent Yorgey and Sean Seefried. Factorization diagrams are so simple and intuitive! A few minutes with the game prototype Robert made will get children comfortable with the diagrams. The two calculators support exploration. The diagrams will appeal to kids who like visual arts, and the game mechanics will help to focus children’s attention. Robert plans to add scoring and badges, and to develop the game for iPad.

How children learn
Do girls have more anxiety than boys? – Asks the Stochastic Scientist
“Contrary to popular convention, girls don’t actually experience more anxiety than boys do during math tests or math classes. They just think they do.” Kathy opens with this surprising finding from a study of German schoolchildren by Thomas Goetz et al. The key differences between the sexes have to do with momentary vs. habitual math anxiety. Read on to see how the same momentary experiences cause different long-term consequences for boys and girls.
Life is a zero-sum game (?) – at Steven Chang’s
Steven looks at the model of life as a zero-sum of some variables, for example: A(career) + B(relationship) + C(finance) + D(character) = 0 – a plane in 4D space. By this model, people cannot be successful in all areas of life, but have to choose what areas of life are important. The assumption that the model resembles real life is not examined.
Sheryl blogs to help adults nurture their youngest children’s sense of wonder. For her, this journey began as a year-long project for Early Childhood Teacher Certification awarded by the American Mathematical Society. It is inspired by Montessori methods and Michael S. Schneider’s book A Beginner’s Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science, A Voyage From 1 To 10. We need to be careful not to let simplicity escape us. Rather than only looking at the numbers 1-10 in the linear fashion, as we ordinarily do, SNAP is an invitation to observe various expressions of each number, individually, across all subject areas, using all of our senses. It is yet another way to support children as they practice careful discrimination, organize thought, and retrieve information in unique ways.
Maria shares her thoughts about Jo Boaler’s How to Learn Math course. “You see, all of our brains actually GROW and make new connections when we make mistakes and think about them. There is no brain growth if you can just sail through a problem set! That is why it is so important for our students to make mistakes — and then we need to VALUE those mistakes and help them learn from them.” Maria also talks about developing fluency through the number sense rather than timed tests.
Fluency and skills
Lilac from Learners in Bloom shares the list of math skills, such as parts of 3D shapes and arithmetic operations, and the corresponding games and activities for kindergarten. Her girls especially enjoyed building “mystery 3D figures” using clue cards that list the shapes of the faces. Lilac takes a list of skills from worksheets, but designs hands-on games and activities to achieve them. There are deeper mathematical bonuses than “just fun”: for example, all building tasks raise questions about different ways you can model the same concept.

Margo offers kindergarten kids a treat: a tactile enactment of addition. It is for the whole child: there’s whole body movement, use of manipulatives, some writing and creativity. Many public schools prohibit holiday parties. However, this party-ish educational activity can be done in the spirit of the holidays, without violating any rules.
Jeremy offers a homemade game, great in its versatility, to practice addition and subtraction. It can also lead to probability. Change the numbers on the die, use negative numbers if you want, change your target numbers… There are many possibilities for DIY fun!
Young children can learn all the math they need through games and activities, agree Julie and her friends. This method can be very motivating, especially when math has been a struggle in the past. Julie links specific games to arithmetic skills they teach. As a big bonus, games also teach strategic thinking, problem-solving, and other valuable mathematical practices.

This genre of puzzles gives kids one letter per exercise. The letters gradually assemble into a phrase. This procedure is a gamification device, that is, an engaging way to track progress and to manage your time and your tasks. Denise shares an exercise she remixed, since the original seemed like nagging. Traditionally, the phrases are funny or cute: they must be rewarding.
Modeling
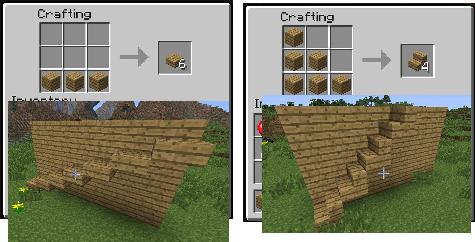
Do you model with physical or virtual objects? Why not both?! Christy invited her eight-year-old to explore positive and negative exponents, and some economics (less material for the same result) with Minecraft crafting tasks, and with plastic tiles. Why are stairs so expensive to make? Why can’t you split stacks into any number of empty inventory slots? Pet peeves in Minecraft lead to tasty math!
How do you improve your number sense? Here’s a list of objects, from tiny to huge. Can you put them in order by increasing size? Where is the biggest gap? How would you measure the gaps? Sue reviews activities and resources from other blogs, and offers her list of interesting, yet well-known objects to sort by size.

See how Fran and her kid used smileys and marine animals for tic-tac-toe? There is much math value in inviting kids to make these design decisions. It helps kids to see the essential elements of the game’s structure in general, abstract ways. In tic-tac-toe, the kid progresses from Xs and Os (a particular case) to two different types of markers (the abstraction). Fran thinks strategy games are a great way to build critical thinking and decision-making skills, as she educates her kid at home. They had a great time making and playing on their own game boards, and thought others would too!

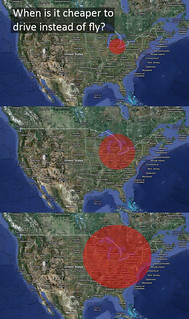
Tom shares full materials for one of the major labs he designed for his Algebra I class. The simple visual sparks interest at a very low entry cost: any student can vote which of the three pictures represents the area where it is cheaper to drive than to fly. Plus, it’s a real life dilemma for anyone who travels regularly! The lab uses spreadsheet tools, such as lines of best fit.
What do math teachers do on vacation? Hint: it involves chalk, a bucket of water, a tennis ball, and math graffiti! Lucy writes: “My kids thought this activity was so much fun! And now my 2nd grader and 5th grader understand the coordinate system.”

Posted in Grow
Inspired by Calculus: Tuesday math circle, week 2
These are notes about a Math Circle we run in Apex, NC. The main goal of this meeting was to explore the idea of limits. But the term “limit” is yet to come up! It’s a deep idea that has to grow slowly enough. In time, I’d like students to be able to:
- Make their own examples of infinite sequences and series
- Make up sequences that have finite limits and series with finite sums
- Use their own examples and words to explain that it takes infinitesimally small pieces for infinity of the pieces to add up to a finite sum
- Draw or make models of repeating decimals (or repeating positional expansions in systems in other bases) as limits, for example, that .9999…=1
Here are our activities, the whys behind them, and things to try at home. Here are all the photos.
- What math do you see in what you love? This combination of a scavenger hunt and a show-and-tell brings home the message that interesting math is everywhere. We searched for math in the “Dungeons and Dragons” book Stephen brought (stats, character progression), and in a woven bracelet Asiyah wore (patterns, infinity). At home: seek interesting math in what you love.

- Hotel Infinity story and finite space. The math motivation is to approach limits. Telling stories together is a friendship-building activity. Classic math stories, such as Hotel Infinity, ground advanced ideas in everyday objects – with some sci-fi, playful twists.

Math is about creating new worlds, so fairy tales and science fiction are very appropriate. At home: read or tell other math stories, such as “The wise man, the king, and the chessboard,” or read the rest of the classic “Hotel Infinity.” I wanted to use the hotel model to ask the question about limits: “Can you make the hotel not take infinite space?” The answer involves deep concepts. I just developed the activity. It was the first time I did the activity with a group, so it was comparatively slow to start, and some kids could not understand my explanation of the task. Next time, I will focus more on modeling the hotel with paper or clay, “to capture infinity in your hand.” Can you build the hotel, here and now? It usually takes two or three tries, at the very least, for a new activity to run to my satisfaction. An interesting question in pedagogy: don’t kids benefit more when they see you doing something for the first time? Some studies say so. It is hard to test new experimental curricula reliably, because volunteer teachers who use a curriculum for the first time are so excited that student learning is through the roof. The same curriculum sometimes becomes less efficient once the teacher learns it well. I like to have a combination of old and new activities, because they have different benefits. - Zombie binary tree. This was our move-around activity for the day. We built a binary tree out of ourselves, pretending to be zombies, because the hands were stretched out front.

Binary tree is a type of a fractal, and a nice photo-op for large groups. At home: show math ideas with your whole body(s) for great photos and videos! Next time, I think I will add a story about the zombie epidemic, with the first zombie infecting the next two, each of them infecting two more and so on.

- Make a square out of paper. Do you measure it out, estimate by eye, or use the diagonal trick? All Maker tasks are full of decisions and problem-solving! Every kid did things differently. At home: invite kids to figure out their own ways to make something, from light saber-shaped pancakes to furniture-and-sheets forts.

- Half of a half of a half. This is another take on limits: a particular example of an infinite series of shapes that takes up finite space. We used our squares. If you cut the square in half, then add half of (the other) half, add half of a half of a half, and so on… What number do you get as your sum?

Maxime came up with a clever way of cutting out corners to show the boundaries better.

The question was hard to express, and the answers varied. You get the whole square! And what number is it? You get infinity pieces. You get one… It was a rich discussion. We will continue next time. At home: cut things into pieces… repeatedly!


- Infinity elephants movie. This is Vi Hart’s artistic take on limits. At home: watch this again, discuss it, watch other Vi Hart’s movies. http://www.youtube.com/watch?v=DK5Z709J2eo
This week, we started quests for parents:
- Just do it. Complete all our activities at your own challenge level. How does it feel? Record your thoughts.
- Tinker, adapt, redesign. For every activity, come up with at least one change. Record your ideas.
- He said, she said. Catch interesting things people say and do. Record what you catch.
Here are the notes from Salima and Kristin (click for full size). Next time, I will provide the list of names with this quest.
Why capture what participants say? An example from the notes – Chris says: “”The size of cut paper will never reach zero, because you can’t split atoms!” This is a representation of a recurring topic of mathematician and engineer takes on math. Chris later asked (paraphrased) if we need to think like mathematicians, imagining the infinite number of pieces in our heads, or like engineers, who know the sequence will stop once pieces get small enough. When we write up this set of materials, the description of this theme will be richer with student quotes.
Another reason to take notes: catching more brilliant ideas. There is a lot going on, so I always miss some beauty. For example, Elena explains the difference between squares and square prisms (after Calvin brings our square-making task into space): “Prisms are hollow inside.” Stephen adds they don’t have to be hollow. Kristin captured that in her notes, and Salima wrote in hers: “It is three-dimensional” – and I remember that Kaiya said that, and then we put “3D” she wrote on a card on the terms board. Only now, reading the notes, I realize that Elena probably used “hollow inside” to point out the third dimension – that prisms have some space inside of them! And then two other kids helped with the terminology and precision. The three of children followed three big math values: exploration, precision, and taxonomic categorization of objects. This process parallels how mathematicians work. At first, you come up with the general idea and your own way to talk about it. As you start talking, your idea and your terminology improve. Yes, we need some space inside a prism, but it does not have to be hollow. Can we say, in general, that it needs to be three-dimensional? I would have missed this beautiful example of math collaboration without the notes. The kids would still benefit, but we need to describe our process for other Math Circle leaders and especially people learning to be leaders.
Kim and Christina took “Just do it” for their quest. I loved to peek into their little adult Circle, with ideas such as infinitely-dimensional space, or time travel, just flying around. There are several networks out there running Math Circles of some sort for grown-ups, notably Martin Gardner’s Celebration of the Mind and Teacher Circles. Why do it? First, doing a Circle for yourself is a joyful experience – a serious game, some meaningful entertainment. Second, doing it helps parents and teachers be more engaged, engaging, and knowledgeable as fellow travelers in their children’s learning journeys. Third, fun with math is therapeutic for people with math anxiety.
Bill was tinkering with activity designs.
Hotel Infinity: add visual aid for rooms and aliens. – This may help to engage children who don’t like to just listen to stories. The danger is “runaway imagery” where kids may remember the aliens, but not the math ideas. This is still worth doing if kids disengage.
When asking for students to draw infinity, take suggestions from kids and draw for them on a large piece of paper, if students have difficulty drawing or initiating dialogue. I will definitely try it this Thursday and especially Friday (with kids 4-6). With a white board, kids can change my imperfect implementations of their stories, as well. I love this idea.
Thanks to all participants for the adventure! See you next week!
Posted in Grow
Guest post: Math for a budding biologist
Karen Samuel Boley is the education director for Budding Biologist, a science ed company created by parents, for parents. Check out their Kickstarter for an ecological video game.
When we think of the convergence of math and science, we think of engineers designing an airfoil or biologists replicating bacteria. At the elementary school level, we tend to picture basic quantities: How much rain fell last month? How high did we build the block tower? It can be difficult to imagine teaching mathematics along with science and going beyond simple measurement.
Mathematical concepts are actually inseparable from science. So inseparable that we use mathematical concepts without even thinking about them. Activities that connect math and science are easy to do in and around your home.

Symmetry is everywhere in nature. Help your child find the lines of symmetry on leaves, and then try it with animals!

By Ernst Haeckel
Natural objects can also be used to illustrate reflections, rotations, and translations – or flips, turns, and slides. How do you move objects to make patterns and design? Children can find tessellations in nature, whether they are on a pineapple, or made by flipping leaves.

Chemistry uses ratios. If we want to make a larger quantity of a compound, we have to add its ingredients in the same proportion, no matter how much we want to make. To explore ratios, children can help with cooking. If you need one cup of rice to serve two people, how many cups do you need if you want to serve four people?
Many young children are familiar with patterns. You can point to patterns in clothing and ask if your child can figure out what would come next. You can show them patterns on animal skin, scales of a snake, the placement of needles on the branch of a pine tree, veins on a leaf, and even the center of a sunflower.

Ask children where else they can find a pattern. Take them on a pattern hunt outside. Use found objects to make your own patterns!

What would continue this pattern?
Integrating math with science activities will show children the practical and artistic uses for math. Doing so addresses the common complaint, “But I’m never going to USE this for anything!” Imagine your children’s shock when they discover they have been using math all along… and never even knew it!
Posted in Make
SAS family math event, September 26th 2013

- We will be planning a fancy tea party – for math. So we can do math with friends!
- I have several grandparents who may be interested in a Math Circle for their grandchildren. We grandparents have good opportunities for math, because we have dedicated time with the children.
- Can we do something mathy with Minecraft? My kids love it!
- I am worried about my girl. How can we help little girls in mathematics?
These are some of the comments from the meeting Yelena McManaman and I led at SAS. We presented our Early Algebra ideas, talked about baby math a bit, and discussed Math Circles. We sold more book than there were people present, since participants bought gifts for friends.
Again and again, we hear that people need know-how and support for forming local, friendly math groups they can enjoy with their kids. We will be helping SAS parents and grandparents with that. How can we help people elsewhere? We need to build stronger networks!
Thanks to Dana Aberhold for organizing the meeting!
Posted in Grow






