Inspired by calculus, grid art, street math: Newsletter October 15
Got this from a friend? Subscribe!
I am Moby Snoodles, and this is my newsletter. Send me your requests, questions and comments at moby@moebiusnoodles.com

Blogs and networks
Two weeks ago, we started several local Math Circles in our new Inspired by Calculus series for kids ages 4 to 10. Read detailed reports at the Moebius Noodles blog, see young math faces, and try it at home.


Our Facebook fans, in response to Robin Angotti’s funky iPad project, discuss childhood math objects that become treasured and special. Nancy Winans writes: “I remember a round plastic purse I had as a child around age 6 – a picture of a girl with the same purse with the same picture of her and it went on and on just like this for several repetitions that I could see. I remember looking at that image many many times and pondering it.” Yelena McManaman adds: “I had a huge collection of buttons and ribbons and I remember sorting and arranging the buttons lots of different ways and building with them, mosaic-style.” Do you remember any math objects from when you were little?

We hosted the Math Teachers at Play blog carnival #67! My personal favorites are modeling tasks like Minecraft optimization, and deep math ideas for young kids, like graph theory with dolls.

What do you see when you look at drawings by little kids? For example, grown-up artists noticed that many young artists draw big heads with legs. The more people talked about these shapes, the more meaning they found. By now developmental psychologists have come up with big theories around these simple observations: “Tadpole drawings appear during the pre-schematic stage…”

Grown-up mathematicians noticed that many young mathematicians draw grids. Round grids, square grids, grids within grids!
Have you kids made any grids? Please send us pictures and stories! See more example in our blog post, Do your little kids draw grids? with masterpieces from Michael Kelly’s son Francis. Thank you to all who sent us grid examples since we posted this!

By request from our newsletter reader Anna Belaschenko, we compiled math projects for the outdoors: 6 BIG adventures in street math.
Events
Yelena McManaman and I held a family math event at SAS. One of the interesting parts of the discussion was brainstorming different Math Circles, from a math tea party for girls to a grandmothers/grandchildren club. It’s always great to try new formats.
Write if you want to have us for an adventurous math event at your place.
Sharing
You are welcome to share the contents of this newsletter online or in print. You can also remix and tweak anything as you wish, as long as you share your creations on the same terms. Please credit MoebiusNoodles.com
More formally, we distribute all Moebius Noodles content under the Creative Commons Attribution-NonCommercial-ShareAlike license: CC BY-NC-SA
Talk to you again on October 30th!
Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter
Inspired by Calculus: Friday math circle, Week 1
These are notes from a Math Circle for children ages 4-5 and their parents. The goal of the first meeting on October 11 was to introduce cycles, iterations, and infinity. We had about a dozen quick activities, half of them from the book Moebius Noodles: Adventurous Math for the Playground Crowd, and the rest newly collected for this Circle.
Here is the set of photos from the Math Circle. I love watching children’s math faces. When children concentrate, or find a new idea delicious, or debate a paradox, their faces are mirrors of their mathematics. At home: pay attention to your children’s math faces. Capture them on camera.
Draw what you like! Say what you like! I try to start every Math Circle with some sort of sharing of what kids like. Sometimes we find math in these lovable things. Value affirmations before challenging journeys help the flow and the overall well-being. Note that some kids were drawing with two hands, as I suggested. You need to tape paper to the table first. This helps with creativity and math thinking, in somewhat indirect ways. I often do this doodle game with kids before doing other math activities.
Introductions. I bonk people on the head (lightly) and they say their name. I started to do it a while ago, because many kids freeze if you point at them and ask them to talk. Nobody freezes if you bonk on the head. This is a very simple example of a very deep math ed principle: use the body to do your math.
Spontaneous activity: Grid pictures. Pictures that look like grids, railroad tracks, wheels with spikes, or concentric circles appear in kid art sometime around the age (or instead of) “tadpole drawings” – and persist from then on. Some kids get a bit obsessed drawing grids! You can read more around the grid pictures at the Moebius Noodles blog. Mathematically, grid pictures are important for multiplication and algebraic laws, such as “distribution” of a line across all other lines. At home: notice if your kids draw grids.
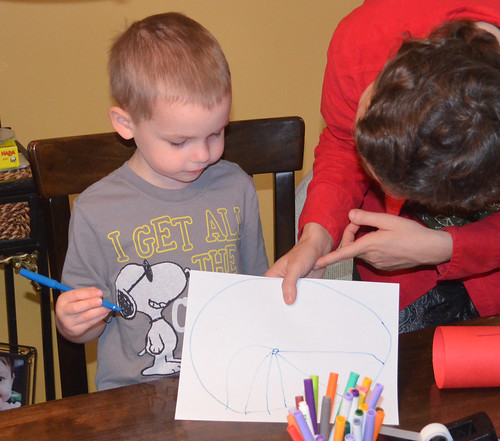
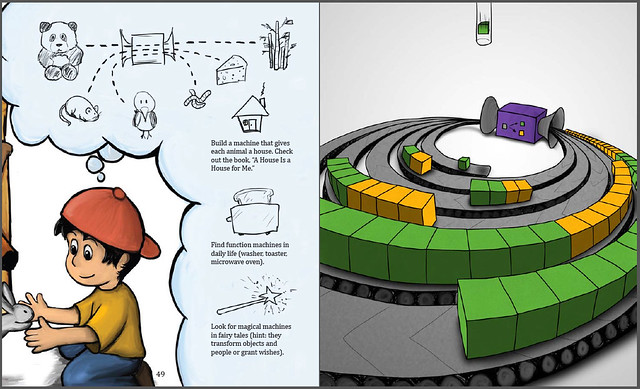
Function machines. We only looked at one function: it added a counter to whatever number of counters we already had. Kids wanted me to “work the machine” again and again and again; Dylan helped to make the machine work. I asked children to draw as many counters as will come out next time, and we checked by placing them over the drawings. Kids need to answer questions by doing, rather than only words. At home: make up your own function machines.

Cut a piece of paper in half… Again and again and again! This is an example of (potentially infinite) iterations. It’s very popular with kids of all ages, even kids who don’t usually like to cut with scissors. Children try to make their pieces as small as possible, or experiment with shapes they can make.

Grown-ups often arrange the pieces nicely, and help children see the patterns. Young ones don’t initiate this patterning, but appreciate it; that’s why mixed-age groups rock. At home: slice or fold more things – again and again and again, into infinitesimal pieces!

Going around in circles. Some kids sat on the table, and Mason and I walked around. Together, we said the name of each kid we met: “Asiya, Lucas, Dylan, Traver, Asiya, Lucas, Dylan, Traver, Asiya, Lucas, Dylan, Traver…” Then we tried with the eyes closed. It’s hard for some kids. Then we tried backwards! It was hard, but Asiya could do it, even with her eyes closed. Doing math with the whole body… Doing math with names… These two simple technique help young kids relate to math! At home: play memory games with repeating patterns your kids make up. Find some situations when repeating patterns happen, such as taking turns in a small group, or frieze designs.
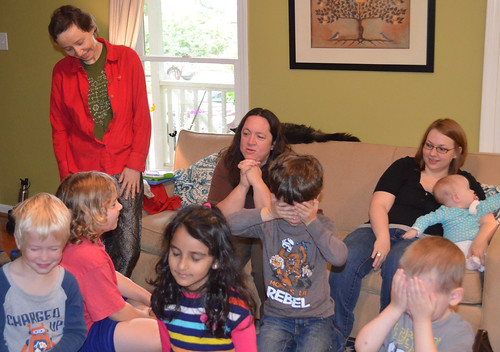
Ring around the rosie… with your eyes closed. Circle games are traditional in many places in the world. They often symbolize cycles of seasons. At home: invite kids to do math with their eyes closed. This simple trick, often used in Montessori activities, helps kids to concentrate, to get in touch with their bodies, and to focus their attention and memory on key math attributes of the situation. It also helps kids to relax and to laugh.

Where do we see things that happen again and again? Kids sort of froze at that question, and I sent them to ask parents. This is something I will do – again and again and again! – in Math Circles wherewhere kids don’t know what to do next, or when we need to deepen our activities. Kids understand their own parents really well, and can explain to the group what parents say. It just felt so good, and it was funny to see families whispering together, and kids were so eager to share the ideas afterwards.

Breakfasts, bedtimes, seasons, sunrises – a lot of iterations revolved around the Sun, so to speak. Notice that kids recognize and appreciate much deeper ideas than they can produce themselves. That’s why we read (more complex books) to kids even after they learn to read, and listen to (more complex) music than we can play, and expose them to more complex math than they would be able to produce! Iterations in your body. I helped kids to observe blinking, breathing, heartbeats – some body functions that happen again and again and again. At home: find more things that happen again and again.
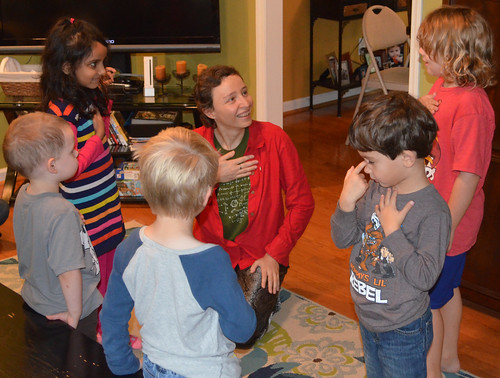
Powers of the universe movie. I usually finish Math Circles with a video. Kids can watch videos even when they are tired; they see complex math in beautiful, accessible ways; and they often share the videos with friends and family. This day, we watched the classic “Powers of Ten.” Mathematically, it’s all about zoom. At home: play with zoom in computers, cameras, or your imagination!
Posted in Grow
Inspired by Calculus: Thursday math circle, Week 2
This week, we tackled the idea that infinitely many things don’t have to add up to infinitely large space. The idea is deep, but young children don’t have the mental resistance to it yet. But they do feel the sense of wonder! In general, you want to introduce ideas early enough that they don’t cause too big a conflict with the kid’s previous thoughts on the Universe…

We have detailed notes about kids – thanks a lot, Lynna and Sally! Here is the link to all the notes. It will help us a lot when we write up these materials for other Circle leaders. Thank you for taking photos, Svetlana! Here is the link to all the photos of this Math Circle.

I am very happy with every participant’s depth of thinking, creativity, and persistence with hard concepts. You probably won’t see me praising kids (or persons in general), because in the long run, it interferes with the flow and the motivation. But I try to praise interesting ideas. And we do see lots and lots of interesting ideas.

What interesting things happened this week? Where is math in there? This combination of a scavenger hunt and a show-and-tell brings home the message that interesting math is everywhere. For example, it’s in the programming of a robotic spider Luca installed at home, and shared by drawing. At home: seek math everywhere!

Does Hotel Infinity take up infinite space? The math motivation is to approach limits. At home: find examples of “infinity pieces” that do, or do not, take up infinite space.

When I did this activity on Tuesday, I asked kids this question in the abstract. This time around, I asked them to draw the model of Hotel Infinity on paper, and see if they can make ALL the rooms fit. We had a curious problem that I (half-jokingly) attribute to gender: all the little boys wanted to expand the space of their hotels, even by attaching extra sheets of paper – rather than “go into” smaller and smaller pieces! But we got a good discussion out of comparing these two scenarios. When do you need more and more paper? Can you fit infinitely many aliens into a finite hotel, if the aliens get smaller and smaller just like rooms? Roman came up with a very meditative doodle method, reminding me of Vi Hart videos: lots and lots and lots of small doors…



In general, kids and the parents doing the Circle had divergent, creative fun with hotel designs – spirals, fractals, going into 3d… We need to expand this design activity some more.
Zombie binary tree. This was our move-around activity for the day. We built a binary tree out of ourselves, pretending to be zombies, because the hands were stretched out front. By this time, kids really wanted to run around, so the activity was a bit hard to do. We need more move-around activities for the younger groups! Binary tree is a type of a fractal, and a nice photo-op for large groups. At home: show math ideas with your whole body(s) for great photos and videos!
Make a square out of paper. It’s a Maker task, and as such, requires design decisions: every kid made a square in a slightly different way. Gray even declared that his full rectangle of paper is a square – I suggested it can definitely happen, on the Hat Planet, that we call that shape “square.” At home: invite kids to figure out their own ways to make something, from light saber-shaped pancakes to furniture-and-sheets forts, and name it in their own ways.

Half of a half of a half. Kids get a lot of joy out of cutting paper smaller and smaller and smaller… So maybe my hypothesis about the need for space expansion is all wrong! Hayden even asked for tweezers to handle the tiny pieces of paper. This is another take on limits: a particular example of an infinite series of shapes that takes up finite space. We used our squares. If you cut the square in half, then add half of (the other) half, add half of a half of a half, and so on… What number do you get as your sum? I am still to ask this question coherently. What I need is a way for kids to come up with a lot of different examples of finite limits. The example where the answer is one is not a good start (even if it’s a good activity): you don’t ever want to start new math concepts from numbers such as 0 or 1.

Even drawing that process on paper (Hayden said it reminded him of the Nautilus) did not help to understand that question. Still, we had a good discussion amid the vagueness! Jeremy thought the sum may be Pi, and Pi definitely has to do with infinite series, being irrational… At home: cut things again and again and again, put them back together, discuss infinity.
Infinity elephants movie. This is Vi Hart’s artistic take on limits. At home: watch this again, discuss it, watch other Vi Hart’s movies. http://www.youtube.com/watch?v=DK5Z709J2eo
Posted in Grow
Math Teachers at Play Blog Carnival #67
Want to write about playful math for the next carnival? See a blog post you like? Submit your links at Math Teachers at Play!

Deep math
Evens and odds at f(t)
Kate usually works with older kids. Following comments from elementary school teachers, she became “a little obsessed” designing a lesson about proofs for young kids. Making deep concepts accessible is an exciting, challenging quest! The post starts with the video about proofs and creativity: what makes us different from computers. It has several visual, hands-on ideas that can introduce proofs to second or third graders. The activities start from students capturing their “noticings,” forming conjectures in Socratic dialogues, and eventually proving the conjecture that odd+odd=even.
Sasha first saw modeling of deep math with dolls at our place, Moebius Noodles. The first challenge Sasha designed for her daughter Katie was to alternate boy and girl dolls, in a story about a ball. With three of each, and six chairs in a line, Katie succeeded. Can you solve the same problem if one more boy arrives? Can you change the degree of all the vertexes in the graph to two, that is, help every doll to have two neighbors, while still alternating boys and girls? Grown-ups know that to change degrees of vertices, you need to change the shape of the graph, that is, to move the chairs into a new configuration. Can a little kid figure it out? Read on!

Robert is building on factorization diagrams, especially on work of Brent Yorgey and Sean Seefried. Factorization diagrams are so simple and intuitive! A few minutes with the game prototype Robert made will get children comfortable with the diagrams. The two calculators support exploration. The diagrams will appeal to kids who like visual arts, and the game mechanics will help to focus children’s attention. Robert plans to add scoring and badges, and to develop the game for iPad.

How children learn
Do girls have more anxiety than boys? – Asks the Stochastic Scientist
“Contrary to popular convention, girls don’t actually experience more anxiety than boys do during math tests or math classes. They just think they do.” Kathy opens with this surprising finding from a study of German schoolchildren by Thomas Goetz et al. The key differences between the sexes have to do with momentary vs. habitual math anxiety. Read on to see how the same momentary experiences cause different long-term consequences for boys and girls.
Life is a zero-sum game (?) – at Steven Chang’s
Steven looks at the model of life as a zero-sum of some variables, for example: A(career) + B(relationship) + C(finance) + D(character) = 0 – a plane in 4D space. By this model, people cannot be successful in all areas of life, but have to choose what areas of life are important. The assumption that the model resembles real life is not examined.
Sheryl blogs to help adults nurture their youngest children’s sense of wonder. For her, this journey began as a year-long project for Early Childhood Teacher Certification awarded by the American Mathematical Society. It is inspired by Montessori methods and Michael S. Schneider’s book A Beginner’s Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science, A Voyage From 1 To 10. We need to be careful not to let simplicity escape us. Rather than only looking at the numbers 1-10 in the linear fashion, as we ordinarily do, SNAP is an invitation to observe various expressions of each number, individually, across all subject areas, using all of our senses. It is yet another way to support children as they practice careful discrimination, organize thought, and retrieve information in unique ways.
Maria shares her thoughts about Jo Boaler’s How to Learn Math course. “You see, all of our brains actually GROW and make new connections when we make mistakes and think about them. There is no brain growth if you can just sail through a problem set! That is why it is so important for our students to make mistakes — and then we need to VALUE those mistakes and help them learn from them.” Maria also talks about developing fluency through the number sense rather than timed tests.
Fluency and skills
Lilac from Learners in Bloom shares the list of math skills, such as parts of 3D shapes and arithmetic operations, and the corresponding games and activities for kindergarten. Her girls especially enjoyed building “mystery 3D figures” using clue cards that list the shapes of the faces. Lilac takes a list of skills from worksheets, but designs hands-on games and activities to achieve them. There are deeper mathematical bonuses than “just fun”: for example, all building tasks raise questions about different ways you can model the same concept.

Margo offers kindergarten kids a treat: a tactile enactment of addition. It is for the whole child: there’s whole body movement, use of manipulatives, some writing and creativity. Many public schools prohibit holiday parties. However, this party-ish educational activity can be done in the spirit of the holidays, without violating any rules.
Jeremy offers a homemade game, great in its versatility, to practice addition and subtraction. It can also lead to probability. Change the numbers on the die, use negative numbers if you want, change your target numbers… There are many possibilities for DIY fun!
Young children can learn all the math they need through games and activities, agree Julie and her friends. This method can be very motivating, especially when math has been a struggle in the past. Julie links specific games to arithmetic skills they teach. As a big bonus, games also teach strategic thinking, problem-solving, and other valuable mathematical practices.

This genre of puzzles gives kids one letter per exercise. The letters gradually assemble into a phrase. This procedure is a gamification device, that is, an engaging way to track progress and to manage your time and your tasks. Denise shares an exercise she remixed, since the original seemed like nagging. Traditionally, the phrases are funny or cute: they must be rewarding.
Modeling
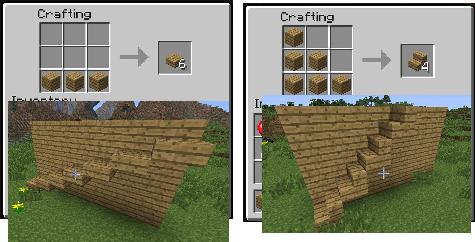
Do you model with physical or virtual objects? Why not both?! Christy invited her eight-year-old to explore positive and negative exponents, and some economics (less material for the same result) with Minecraft crafting tasks, and with plastic tiles. Why are stairs so expensive to make? Why can’t you split stacks into any number of empty inventory slots? Pet peeves in Minecraft lead to tasty math!

How do you improve your number sense? Here’s a list of objects, from tiny to huge. Can you put them in order by increasing size? Where is the biggest gap? How would you measure the gaps? Sue reviews activities and resources from other blogs, and offers her list of interesting, yet well-known objects to sort by size.

See how Fran and her kid used smileys and marine animals for tic-tac-toe? There is much math value in inviting kids to make these design decisions. It helps kids to see the essential elements of the game’s structure in general, abstract ways. In tic-tac-toe, the kid progresses from Xs and Os (a particular case) to two different types of markers (the abstraction). Fran thinks strategy games are a great way to build critical thinking and decision-making skills, as she educates her kid at home. They had a great time making and playing on their own game boards, and thought others would too!

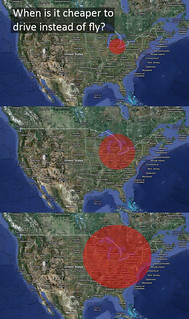
Tom shares full materials for one of the major labs he designed for his Algebra I class. The simple visual sparks interest at a very low entry cost: any student can vote which of the three pictures represents the area where it is cheaper to drive than to fly. Plus, it’s a real life dilemma for anyone who travels regularly! The lab uses spreadsheet tools, such as lines of best fit.
What do math teachers do on vacation? Hint: it involves chalk, a bucket of water, a tennis ball, and math graffiti! Lucy writes: “My kids thought this activity was so much fun! And now my 2nd grader and 5th grader understand the coordinate system.”

Posted in Grow




