Inspired by calculus: Tuesday math circles, Weeks 4 and 5

These are notes about a math circle for kids ages six to ten. Thank you for your write-ups, Kristin and Sally! All photos are in the set on Flickr.

This time, I talk about several activities that did not work as I hoped. In hindsight, I think I know how to fix the experiences, and what to avoid in the future. I am sharing these notes to help parents and designers, and to ask for input. Please tell me what you think on how to improve, and ask your kids. Even knowing such experiences are necessary for innovation, it’s hard for me to write about experiments that fizzle.

There is an endless list of design issues that make activities go south, for example, the room is too small, the rules are too numerous, not enough storytelling to feed the imagination, manipulatives distracting from ideas, and so on. There are many checks and balances between too much and too little of this and that. But if children have enough freedom, and sympathetic adults, most of the time they just self-regulate in all these aspects!

There are three levels of freedom in activities I choose or design. As a side note, the lowest level is more freedom that many textbooks or classes ever give students.

1. Problem Solving. Students receive problems with known answers. They have the freedom to use, develop, or acquire any method of solving the problems.
2. Inquiry. Students receive open-ended problems with infinite possible answers. They have the freedom to interpret the nature of answers, as well as choose methods of solving the problems.
3. Self-Organized Learning. Students choose (or accept an offer of) a broad starting area, and pose problems or projects within that area. They have the freedom to make their own problems, to interpret the nature of answers, and to choose methods of solving their problems.

For example, the task of drawing infinity is at the third level, and the task of drawing Hotel Infinity so that all infinity rooms fit on paper is at the second level. I need to try harder for more third-level tasks. Impose too many restrictions (as in the shape tasks below), and you are in the first level territory, or even lower! Ouch!

Shape out of similar shapes. The goal of this puzzle is to connect partitioning and grouping. We have been doing a lot of partitioning activities, splitting shapes into infinitely many pieces. Can kids reverse the process? I asked kids to make a shape out of similar shapes, but not infinitely many of them. This was an engaging, meaningful activity that I will use again. The fact it’s rather challenging, and takes a long time, is surprising, since we did a lot of “take shape apart” activities before. But any sort of reversal is challenging for kids. For example, if you introduce addition separately from subtraction, children find subtraction much harder to do. Taking square roots is often harder than squaring. I want kids to see seamless connections between partitioning and grouping, for example, positive and negative powers of ten, or fractions and multiples.

I loved that some kids made shapes out of one single shape, for example, a square made out of one square. This is an example of an extreme case. Looking at extreme cases is a valuable math practice, because you often notice new properties when you look at extreme cases. Kids who love to find loopholes in rules are especially strong at this math practice. Support it.

Another emergent behavior was to make “zoom shapes” or “frame shapes” that looked like nested dolls. I have tried the “shape out of shapes” activity with four groups of kids so far, and this idea came up in all four.

There are two strong math principles behind it. First, it works with absolutely any shape; the idea is powerful because it’s universal. Mathematicians always strife to make conjectures or rules apply to as many things at once as possible. That’s how they figure out how to take square roots of negative numbers, or divide by zero. The second powerful principle is from calculus. A nested shape consists of infinitely many infinitesimal thin strips. The same idea of thin strips is behind numeric integration. I don’t know yet how to turn this into a separate activity, but I will keep thinking about it. Maybe when we get to integration!

Formal rules: shape out of shapes. I told kids the next round of the puzzle will be more challenging. Here were the restriction to up the challenge:

1. The big shape has to be the same type (e.g. a rectangle or a triangle) as the little shapes.
2. No gaps or overlaps!
3. The big shape is made out of two to ten little shapes.

The goal of the restrictions was to approach a particular math topic, namely, decimal fractions and the corresponding fractions in different bases. I wanted to share my fascination with things like .9999…=1 and the whole idea of positional system viewed from the calculus perspective. But these ideas, in the form I tried to approach them, required rather narrow and symbolic path to them. For example, I narrowed down the requirement to make big shapes out of small enough number of little shapes, because I wanted kids to do the sub-divisions again and again and again. This I could not communicate, and so it came across nitpicky and random, and kids just did not follow. They continued with various doodles of infinitesimal shapes.

I think they suspected I am trying to take them out of the realm of calculus and into the realm of arithmetic, and resisted that. The three rules became more tedious than challenging. Even the idea of making a movie about the shapes was only momentarily exciting.

Shapes out of shapes: now with the story and a maker component. The week after, I attempted to salvage the activity by adding two components that generally make activities more alive. First, we tied it to the story of Hotel Infinity. Kids were to draw a group of 1-3 aliens that would go into one of the three hotels. Then kids were to make up a symbol for the type of the rooms within the hotel. It worked better, because stories and making things up are good to have, but there is still room for improvement.

Minuses: making up symbols for counting numbers wasn’t really enough of a maker activity for calculus, and wasn’t puzzling enough to make for strong problem-solving. Conclusion: increase the problem-solving (puzzle) component; clarify and strengthen the idea of symbols; and scaffold children’s attention to the development of the positional systems via a series of puzzles that can lead to better discussions of infinitesimals. Here are my notes for the future:

1. First, go on a scavenger hunt for all sorts of symbols. Just telling kids “make up alien symbols” was too sudden, and required too much backtracking into what symbols are, anyway! But hunting for symbols is a fun activity for people of all ages. I’ve done it with groups before. My teen has done it in a philosophy class.
2. Stick with one hotel at a time, but invite kids to pick one room instead of a group of rooms. I’ve done a variation of this with a group of kids at the MusArt camp, and it worked fast enough (~10 minutes) and was fun enough that they wanted to keep going longer than I did. So I could introduce multiple hotels next. This would lead kids into their own versions of positional systems with symbols. I think starting with Base 2 would work the best, because you only need to indicate the level within the hotel (the position) – like using 1 in a particular position in a binary number. Then we could make the puzzle harder by using Base 3, Base 5, Base 10… And ask kids to contribute shape ideas when hotels are built, so we can use someone’s favorite shapes.
3. Add a stronger maker component focused on sequences and series, infinitesimals, or other related calculus ideas. I am not sure how to do this, yet. I think creating your own sequence may be engaging. At least if you judge by thousands upon thousands of submissions in the Online Encyclopedia of Integer Sequences. I want kids to be creative with what they make – using drawings and models, not just numbers. It’s not clear to me yet how to promote this aspect.

I later noticed that several kids used spatial symbols, for example, Chris used a planet with a ring for the sixths level (hint: Saturn), Ben used a flag to mean the top level, and Calvin used up-arrows to show that the alien can change its size and also needs to occupy the top level.

Jason and Kim both used objects to indicate the third level; they discuss their work with one another a lot, and sometimes their ideas develop together.

Other kids used number or quantity symbols: Maxime x4, Elena the mirror 1, Kaiya +2 and Asiyah two pumpkins. Stephen used 1 2 3 to indicate the third level.

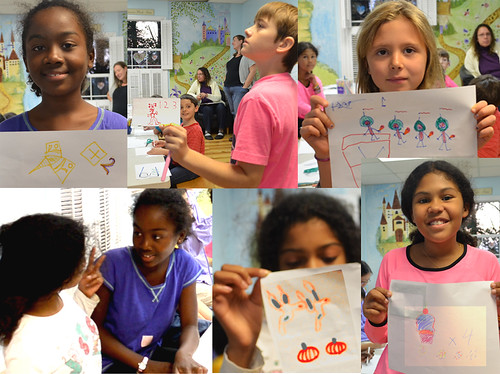
It is a joy to see ideas spread. I am happy the kids pinpointed the essential idea that levels of the power structure can be numbered, and came up with a variety of symbols. At home: come up with symbols for various ideas.

The Zeno walk. Can you reach the camera? What about all the infinity halves you have to pass? Zeno paradoxes are resolved through calculus. For example, the arrow paradox we roleplayed is resolved if you realize infinitely many time intervals can add up to a finite time total. And kids did explain this idea, in their own words. They weren’t very surprised, either. Some of the calculus ideas that baffle adults seem easy, almost trivial to kids. Wow.

Interactive: Universcale. I think the above activities helped kids to engage with the Universcale interactive at a deeper level. At home: find systems that zoom in and out, split or group, such as measurement units.