1001 Leaders: EuclidKids LLC begins as a friend helps a friend’s 5 year old
 Marcia Cooke is the author of two beautiful toys, called Powers of Two and Binomial Squares. They can be used to explore infinity, series, multiplication and proportions, place value, and equations with young children. Marcia likes to meet children and parents to play math together. From the vantage point of a high school teacher, Marcia shares her wisdom about playful, deep, beautiful mathematics with young children.
Marcia Cooke is the author of two beautiful toys, called Powers of Two and Binomial Squares. They can be used to explore infinity, series, multiplication and proportions, place value, and equations with young children. Marcia likes to meet children and parents to play math together. From the vantage point of a high school teacher, Marcia shares her wisdom about playful, deep, beautiful mathematics with young children.
In our 1001 Circles series, we feature math circles stories from the point of view of a circle leader, who acts as an invisible tour guide. In 1001 Leaders, the companion series to our 1001 Circles, we put the spotlight on the leaders themselves. What got them started and what keeps them going? What are their math dreams and worries? If you lead a math circle, an engineering club, or an informal playgroup, we would like to hear your story or interview you. Write moby@moebiusnoodles.com to talk about your adventures.
How did you get into design for young children?
My teaching career is unusual. I am a high school teacher, but I started as an elementary school teacher with an extensive background in using manipulatives. I took higher-level university math courses, but it was my own learning to use manipulatives, and observing children, that made a big difference. All of a sudden I found math learning so much easier, and intuitive. I think that’s because in my own mind, math understanding was not restricted to symbols, but expanded to dimensions and images. It made it easier for me to understand high-level mathematics. Gradually, I went into high school teaching, and became the chair of the math department.
Our history teacher asked about good mathematics for her 5 year old. Together, we invented the puzzles. Then her husband said we should form a company, EuclidKids LLC, because the puzzles had so much effect on their daughter’s learning. The puzzles are very similar to Key Curriculum pieces in the 1980s. I used to play those games with my 1st graders, and a disproportionate amount went to be very, very good students. This knowledge has been around, but people are not using it enough. Maybe because it’s more suited to homeschool or Montessori than a traditional classroom.


Can you give an example of what you understood through manipulatives?
There are so many instances when my own study of mathematics has been improved by learning to use math manipulatives, and they are so varied that I am having trouble making a brief response. Trading games and grouping activities help 5-7 year olds understand place value. Place value concepts are based on exponents and geometry – the connection I saw through manipulatives.
If we think of x as a length, then x2 is a square region, x units wide by x units in length. Similarly, x3 is a cube, x units long, x units wide, and x units deep. Even learning to use base-ten blocks to understand place value and regrouping adds a spatial reasoning element that deepens mathematical understanding.
What are the trading games you mentioned?
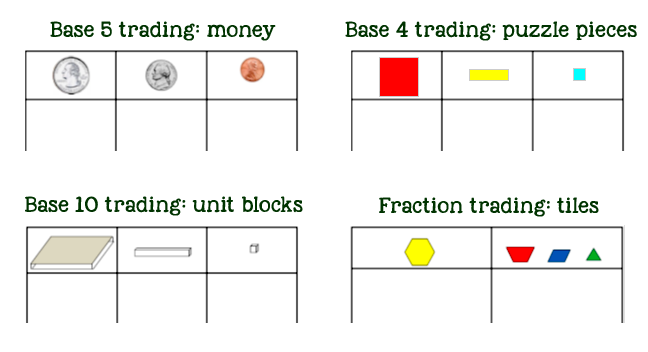
One to three children sit in front of an adult “banker.” The children have a place value mat in front of them. This mat is divided into 2 to 4 place value columns. The column farthest to the right is the ones column. When a player rolls the die or spins a spinner to determine how much, the banker pays her in ones. When she has the base number of ones, the player trades for the next unit. The base number can be adjusted to the developmental level of the child. For example, a pre-kindergarten student might play in base-five using a mat with column headings depicting pennies, nickels, and quarters. Six and seven year olds can play base-ten games. Children can also play with fraction pieces and wholes. The winner is the first child to obtain the agreed-upon number of the objects in the leftmost columns, such as two quarters or five hexagons.
What is it all about for you? What will change in the world when more people use these approaches?
In educating young children, we tend to think of teaching them numbers and counting. We teach them numbers in terms of quantity. Of course, quantity is important, as well as associating quantity with symbol. Math is equally a study of dimension. When you introduce young children to the area model, they focus on the length of the sides (1D), and the area of the region that is filled in (2D). From the first, second, and third dimensions, exponents come in. This way children operate on objects with their hands! You help young children to create visual imagery that later will suddenly make sense in algebra courses, and become associated with expressions like x2.

Children who engage in spatial reasoning tasks do better in advanced math courses. The goal of calculus courses is to help students associate symbolic reasoning with images. For example, an equation with its graph. Manipulatives help students integrate counting and measuring, as in many historic uses of mathematics. Even long ago, people weren’t just counting: they also had to measure distances and land. This bridge is ancient. Something that starts as pretty and interesting to young children is helping to create the visual imagery they need later on.
There is an element of beauty that mathematicians talk about. When we play with binomial squares with young children, we are just talking at first: here is dark red, light red… What colors are pretty together? That grows into associating intensity of the color with the size of the piece. The color varies, and the size is another variable. A Montessori education is all about helping young kids develop their powers of observation – even at the beginning, when children see the puzzle not mathematically, but as a piece of art, and enjoy rearranging it.

Picture: two-variable (covariation) games from the Moebius Noodles book
What will be different for young children who have had these experiences? They will find mathematical learning more intuitive. They will ask their own questions, such as, “How many squares can you make from the puzzle pieces?” Instead of place value being explained to them verbally, it will come naturally, or the verbal explanation will make perfect sense. There will be less anxiety about math learning.
Perimeter and area are too often taught by rote, but they can be taught intuitively. Children can see and feel perimeter as the edge of the square, and area as the two-dimensional space within. Kids have difficulty – many, many kids do – because we focus on counting. That is, we focus on number as a count instead of number as a length. For example, the document for the Common Core geometry standards has an image that is similar to the binomial square puzzle. This image is used for teaching fourth graders to multiply 1 1/4 by 1 1/4. Students often think the answer is 1 1/16, but it is not. It’s a four-part multiplication, which is intuitive with the area model. 1*1, 1*1/4, 1/4*1, and 1/4*1/4 are the four products you need to add up. The puzzle can be used to teach why.

What are the benefits of advanced ideas like dimensions, or different bases in the trading game?
I believe adults should not use the Binomial Squares and Powers of Two puzzles to impose higher levels of teaching upon young children. It would take the joy out! These are universal ideas that any person can understand: dimension and space. Allow children to enjoy the puzzle, interact with the puzzle, and put it together in many different ways… Later, you may ask some questions, similar to the questions kids ask: “How many squares can you make?” You can play a base 4 trading game. For example, if the small square is 4, then the big square is 16, because it fits that many small squares (four by four). This helps to introduce place value just by playing the little game. These manipulatives integrate counting, measurement, and dimensions. Hopefully, the child will associate the learning with pleasant, exciting time of exploration later in life.
How do you know when the time is right to start asking questions?
When a child responds to the question with interest and engagement, that’s the right time. If the child ignores the question, it means she is not ready to engage in that way. One of the wonderful things about trading games is that I have never known a child between the ages of 5 and 7 who doesn’t love them, and as the grown-ups share that joy, they are also learning how to ask questions.

If a 5 year old is enjoying putting puzzle together, it is not a good time for questions. If the child is focused on the colors, she may not respond to questions about other topics, such as “Can you put together squares made of different pieces?” Ask questions about what the child is paying attention to.
Here are sample questions from our materials that accompany the Binomial Squares puzzle.
- Explore combinations
- How many ways can the puzzle be put together with the little squares at the center?
- How many ways can the puzzle be put together with the big squares at the center?
- Problem solving
- Can you make a square using four pieces?
- Can you make a square using nine pieces?
- Proportional reasoning
- How many small squares make up a rectangle?
- How many rectangles make up large square?
Ask more open-ended questions. Jerome Bruner had a wonderful research project with children ages 5 to 7. He divided the subjects into two groups. The task was to fetch a piece of chalk from a transparent box without leaving your seat. He gave the children short rods, connecting clamps, and hooks. In one group, he taught children how to retrieve the chalk. In the other, he gave the kids the materials and let them play without explaining or demonstrating. Only after they played did he ask them to get the chalk. In the first group, children gave up if they did not succeed immediately. But in the second group, children were more inventive: they made multiple attempts, with different strategies.
In his book The Process of Education Bruner argued that even young children could engage with challenging material. In his constructivist model children approached such material through three stages: handling materials, forming visual images, and using symbols – in his terms, enactively, iconically, and symbolically. Bruner, who taught for many years at the Harvard School of Education, advocated “a science of toys.” Such toys give opportunities for physical manipulation that leads young minds to form images.

I know other researchers say manipulatives are not magic: that they don’t do any good if adults don’t structure learning in some way. That’s why in Montessori schools teachers ask questions. I say even playing with the visual imagery alone will be a benefit.
Research says that one of the perceptual differences between adults and young children is that children tend to pick out one feature of the puzzle, such as color, and focus on it. In other words, they have trouble integrating different qualities of the object. That’s why I am opposed to things like teddy bear counters. Yes, they are adorable, kids enjoy them, but they can also distract children from the idea of counting, because they may be thinking about teddy bears. Children older than 7 are much more capable of interacting with physical objects in multiple ways.

Will children focus on different qualities of objects on different days?
I would say yes, definitely, but I don’t know if it is days, weeks, or months. It could be a long time for young kids. I have seen kids interact very intensely with the puzzle over several days, and be very interested, then not interested for months. They come back in six months or a year later, ready for questions like, “How many small squares equal the rectangle?” The puzzle’s use as a learning tool is spread over several years.
Related Posts
Posted in A Math Circle Journey, Make







This is such a find for me. I appreciate, so much, someone with a both a math background and a Montessori background blending approaches, seemingly, channeling Maria Montessori and taking things beyond where Maria had to stop.
I would love to know who Marcia Cooke works with and if she works with Montessorians, researchers, etc.
So many juicy tidbits in this interview:
Children who engage in spatial reasoning tasks do better in advanced math courses.
. . . education is all about helping young kids develop their powers of observation – even at the beginning, when children see the puzzle not mathematically, but as a piece of art, and enjoy rearranging it.
. . . mathematical learning more intuitive.
. . . less anxiety about math learning.
. . . opportunities for physical manipulation that leads young minds to form images.
. . . playing with the visual imagery alone will be a benefit.
The puzzle’s use as a learning tool is spread over several years.