Bojagi: Cute multiplication puzzles by and for families
Multiplication is not just repeated addition, but what is it? From Montessori beads to algebra tiles, many developers claim the array and area models are great for growing children’s conceptual understanding and fluency in multiplication. You can go on scavenger hunts for the area model in tiles and bricks, and draw your own models using graph paper or computers.
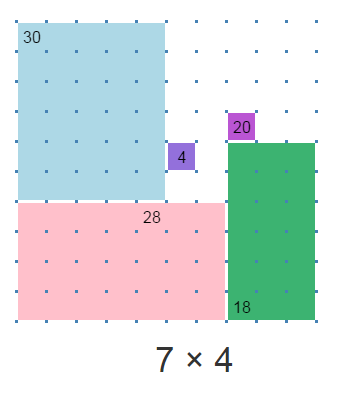
The new puzzle game Bojagi by David Radcliffe (@daveinstpaul) is all about drawing areas. Bojagi’s puzzles make you think, but the rules are easy. Draw a rectangle around each number by clicking and dragging with a mouse. Each rectangle should contain exactly one number, and the area of the rectangle should be the number that it contains. Rectangles must not overlap.
As you draw, the game tells you the two dimensions of your shape, for example, 7 x 4. If you break the rules, your shape disappears. The puzzles provide meditative fun for grown-ups and kids alike. The game helps kids learn multiplication in a gentle, playful manner. Making your own puzzles also feels great: you can draw designs, demonstrate algebraic formulas, or simply play with shapes in open-ended ways. A family or a math circle can take turns designing puzzles for one another.
You can find all the puzzles made so far in a big list, and add your own using the puzzle creator. Here are three quick puzzles I made when I first started playing:
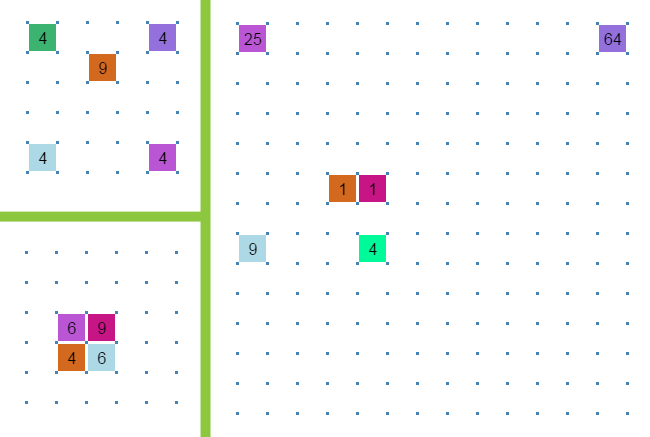
- Not Squares has only square numbers, 4 and 9.
- The Fib is about the Fibonacci sequence.
- A Plus B Squared shows the four natural parts of the area that is 2+3 units by 2+3 units.
Bojagi demonstrates these design principles:
- Intrinsic learning. The area model of multiplication is the foundation of gameplay and tactics: you can’t make Bojagi without it. This is in contrast with extrinsic games, where computations are separate from the game mechanics (for example, correct answers let you explode monsters).
- Answer-first approach. You are given the result of the multiplication, rather than numbers to multiply. The task is to “reverse-engineer” the result.
- Strategic problem-solving. Not only do you need to find individual areas correctly, but these areas must also fit the whole puzzle. If they don’t, you have to retrace your steps and try the puzzle again. When solving good math problems, not only do you need to solve each step correctly, as in an exercise, but also to devise an overall strategy that works.
- Make your own math. The puzzle creator supports free play and open design of your own patterns.
Here is my interview with Bojagi’s creator, David Radcliffe.
 Please tell us a bit about yourself.
Please tell us a bit about yourself.
I am a college math instructor who is changing careers to software development. I graduated from the University of Wisconsin-Milwaukee with a Ph.D. in mathematics. I am interested in finding new ways to use software to help students learn mathematics, especially the tools that encourage exploration and creativity, not just memorization and skill development.
What is the motivation behind your game?
My game presents multiplication in a meaningful context: the area model. I think that it will help students to memorize multiplication facts, but also to understand them visually. It was very important to me that students should be able to create their own levels and share them with their friends, because I want to encourage exploration and play.
Many people say the area model is their favorite model of multiplication. What about you?
The area model is my favorite model of multiplication because it is so easy to visualize. The area model makes many of the properties of multiplication clear, such as the commutative and distributive properties. One weakness of the area model is that it is difficult to interpret multiplication with negative numbers using this model. In that case, I prefer to describe multiplication as scaling.
Your game has a lot of bridges to ideas. Can you name a few?
Besides practicing multiplication facts, the game can be used to explore factorization, divisibility, and prime and composite numbers. A child playing this game can discover that prime numbers can be covered by only one kind of rectangle. Kids may be led to ask which numbers can be covered by two kinds of rectangles. This line of investigation quickly leads to some very interesting concepts in number theory.

(This is a screenshot I took while making a puzzle that can lead someone to explore different ways to factor the same number – MariaD)
Anything else you would like to add, David?
I am a fan of your work with Moebius Noodles, so I am very happy that you are interested in my game. I would be glad to answer any questions that you have. Also, if you have any great ideas for games that I could implement, please pass them along.
Please leave questions and game ideas for David in the comments!
PLAY BOJAGI
Related Posts
Posted in Make







Really wonderful game and fantastic implementation. I’ve had my eye out for a game that intrinsically uses multiplication facts and I love this puzzle. Also, making it so easy for users to create their own puzzles was a great idea and I hope to see it again in a lot of other games/puzzles.
So fun to do puzzles and get the whole family involved! Great interview!
Thank you, Lisa. What did you family like about it? Did your child noticed anything cute?
This is originally a Japanese puzzle that I’ve seen many times in Japanese puzzle books:
http://shikakuroom.com
Credit should be given.
The website for Bojagi is not working. I would love to use this resource with my students! Is there a new link? Thank you
Emma,
I fixed the links to lead to the new website, bojagi.us I hope your students enjoy making and solving the puzzles. Thank you for letting me know the links changed!