These are notes about our activities at the third meeting of the Math Circle. The main goals of activities were to contrast linear and non-linear growth, and to approximate curves with straight lines. Children’s activities brought my attention to three other ideas: consistency of patterns; differences; and measurement.

Here are all photos from the Circle. Yelena took notes (here they are) and Sally took photos this day – big thanks, ladies!

Fractal lichen. Mark found fractals and infinity in gray lichen. Every meeting, we find math in interesting objects. Do try it at home.

New words in what we did the last time. We talked about the activities from the last time. Gray suggested the word “smallz” to describe objects that grow smaller and smaller and smaller. I brought up the old long word “infinitesimal.” I think kids like “smallz” better. It has a nice ring to it! I asked kids to come up with examples of infinitesimal things. They got stuck, I sent them to ask parents. It’s a good lifetime practice to go ask your elders. Examples: squares (from the last time), Hotel Infinity rooms, bacteria… At home: search for infinitesimals; invite your kids to name their ideas.

Guess my pattern. I should have invited kids to make growth patterns of any sort, but I first invited them to guess what comes next in my pattern (1, 3, _). Guessing particular patterns before building your own causes two issues. First, it does not allow kids to work out the idea of consistency, which is easier if they are free to build any pattern they want. So we had to work on consistency too much.

Second, kids always want and need free play before they work systematically. Guessing someone else’s pattern is systematic. So children built their own patterns anyway, in the background, as we worked on my rule… At home: take turns guessing patterns you build, but let the kids build theirs first, any way they want!

Building patterns. I asked children to build a growing pattern “all in one line.” Note Hayden building complex shapes that formally follow this rule! We then checked if tops of each column formed straight lines or not. At home: come up with stories about things that look like histograms or growing columns. I am thinking of supporting columns for roller coasters. We need more motivation to look at this type of graphs. Kids assumed “linear is good” – Jeremy was somewhat concerned his pattern that grew by 1, 2, 1, 2… wasn’t linear. Again, we need story motivations for when we want linear and non-linear patterns to happen. Roller coasters? Skylines? Meanwhile, kids focused on differences from one column of LEGO to the next. Difference equations and the attention to differences (“deltas”) are key ideas in calculus. We will work on these ideas some more. Slopes (derivatives) have to do with differences!

Seeking straight lines. We went outside to look at straight and curvy lines – that was our “move-around” activity for the day. My hypothesis was that most straight lines were human-made. Kids found many straight lines in nature: blades of grass, leaf veins, and the flat ground (“technically not human-made” – Jeremy).

The ground example surprised me, because it’s not a line but a surface (a plane). Jeremy extrapolated the idea of lines to the next dimension. At home: look for human-made and naturally occurring straight lines, curves, planes, and curved surfaces.

The doubling pattern. This activity illustrates the simple principle of learning math: don’t show, don’t tell, but help to do. I invited kids to make a pattern where every next column is twice as high as the previous one. Telling was confusing. I started to build the example, with four columns. Showing my example was confusing too. Extra explanations did not work… Then grown-ups helped each kid to make two columns as high as the last one in the sequence, and stack them to make the next column in the sequence. Bingo!

Kids were very involved in this exponential growth, and making their towers higher and higher. They even took apart their past freeform creations to have enough blocks for tall towers. After a good while of playing with this amazing pattern, I asked kids to go through it backwards. Smaller and smaller and smaller, 8, 4, 2, 1… Then what? Jeremy: “If you had another type of brick…” I asked kids to imagine bricks getting thinner and thinner and thinner. Infinitesimal bricks. They were quiet for a while, imagining, thinking.

Runaway measurement. While measurements or counting are not the goals of these meetings, kids keep bringing them up. “This column is almost as long as my leg!” – this expresses the surprise at the speed of exponential growth. The length is more tangible if you compare it to familiar objects, as journalists often do. We used rulers to see if lines were straight or curved, but kids also wanted to measure the lengths of their LEGO columns. “My column is literally as tall as yours” (Gray) – with some hint of wonder. The fact that the same rule (doubling) produces the same outputs every time is not quite obvious, at least not in its applications. We probably need to do more measurement activities, since it’s a big interest. At home: check out the Universcale interactive for relative measurements in our universe; look for examples of exponential growth.

From polygons to circles. Adding more and more sides to a regular polygon makes it look closer and closer to a circle. Jeremy: “Interesting that you started doing this as soon as I mentioned Pi!” Me: “That’s because you keep mentioning Pi, and I prepared a Pi-related activity.” At home: look for more examples of how straight lines can form curves.

Video of the day: Sierpinski Dream.

Notes from home: Lynna sent a couple of observations. It’s always interesting to see what discussions happen at home! Do share what you do, and what kids say.

Maria – we stopped on the way to math tonight and our car wont restart. We are awaiting help and are sad to miss our wonderful class this evening. We are having an interesting discussion about zero and negative integers after he said that numbers have a beginning at 1 and go on forever to infinity in one direction.

 I had to share the saying on my tea bag this morning with you ~ Act selfless, you will be infinite.  Once we start thinking of these ideas we start to notice them everywhere!

Please shoot me a quick email if kids do or say anything related to functions, infinity, and other such topics, at home. It really helps to plan for the next time, and it’s always interesting!

Thank you for taking notes, Kristin, Bill, and Guy! I use full notes for write-ups. And thank you everyone who helped with photos. Here is our full photo set.

Share something you love. Ben brought a set of building magnets. Kids found geometry and infinity in it.

Kim built a hexagon out of small counters, and kids found infinity in it.

Maxime made the diagram of her family tree (it’s a binary tree, like we made last time) – and said that family, and people, can go to infinity. Kids grew their math eyes: now they see infinity everywhere!

What did we do last time? This is an activity about math terms, and about math connections. As kids recall what we did, I ask them if they want to add math words to our board. As a participant, I get my turn adding words, too. You probably noticed that we take turns a lot. Grown-ups often share the knowledge of past generations (existing math) when it’s their turn. Children often make something up, or at least make new connections. Even on mundane tasks such as naming terms, we can expect the unexpected from children’s divergent thinking and creativity. Tradition+creation=progress. At home: try to find some of our math words in the world around you.

Use counters to guess function machines. Three counters go in, and five come out. Four go in and five come out. Can you guess the rule? Children created their own machines and guessed one another’s rules. The goal is to connect the idea of function to calculus ideas, such as limits. At home: play the function machine game without counters, just giving inputs and outputs as numbers. Or use objects of your choice to model function machines.

Negative zero? This was a short spontaneous discussion from something Stephen said. None of the kids had ideas on what a negative zero could mean. That’s one reason I invite parents to participate. Alicia suggested approaching zero from the left (on the number line). Children liked the idea! It will come handy later, when we work more with limits. Kids often say weird things that you can unfold into interesting, deep math.

Accidentally, exponents! “What I noticed today: when kids worked with LEGOs, they made these exponential functions…” – Alicia told me after the Circle was over. This observation, and our conversation about it, started a train of thought I’d like to share.

When we worked with the counters and drawings of “function machines,” all kids designed linear functions. Their machines multiplied or divided by a number; or their machines added or subtracted a number. This is a consequence of the existing math curricula and math materials. Even if kids have been exposed to non-linearity, as I am sure all these kids have been, the bulk of their number fluency is linear.

The task was to build LEGO towers out of our function machines: bar graphs, though we did not use the term. The first tower was the output for the input of 0, the next for the input of 1, the next for the input of 2, and so on. But this is not what most kids actually did! When working with LEGO, most children used their formulas recursively: that is, they applied the rule to the previous output.

There are two strokes of genius in this change the kids made. First, iterations greatly simplify the structure of input-output functions. Instead of keeping accounts of two series of numbers (inputs and outputs), and their connections (this input for that output)… Children only need to keep track of one series that builds on itself. Here are side-by-side comparisons for Kaiya’s rule (+5) and for Jason’s rule (*3), with the towers they made.

Elena came up with a hybrid way to represent patterns. “One goes in, two comes out… Two goes in, four comes out…” She iterated x2, but she represented both inputs and outputs in one line: 1, 2, 2, 4… The horses were doubling, too.

If you count the LEGO bricks in the pictures, you will see some of the patterns change mid-way. Are these mistakes? Why didn’t we fix them? Most of the time, you see breaks and mistakes in patterns when kids get a bright idea. Kids can either chase a new idea, or keep the old pattern going, but there is not enough both. Do not pay too much attention to mistakes – instead, ask kids what they are thinking. You can chase the new idea together, and fix the pattern later. All the kids in this group pointed out breaks in their patterns. Don’t be afraid children will forever miss a mistake. Losing new ideas is more dangerous.

Chris wanted only whole numbers to come out of his function machine that divided by three. So he skipped the inputs of zero, one, two… four, five… seven, eight… and so on. Kids often have very particular wishes about domains of their functions, either because they prefer computations to be nice, or for aesthetic reasons.

Malcolm used volume rather than height to represent his function, because there weren’t enough bricks, he said. We may follow up on that idea and do more with volumes next time. Yay for creative solutions!

“Make things as simple as possible, but not simpler” – Einstein explains about a core principle of math and science. To make things simple, you often kick the abstraction up a notch. Kaiya: “It starts with two [this is a choice; she could start with any number – Maria], and goes to [pauses to check again] seven, which is five more. And then it goes to five more than that… whatever it is. And five more than that, again.” Note the phrase – whatever it is – a child’s way to describe variables. This is the language of abstraction, of algebra or calculus. We don’t care as much about particular numbers, as we do about the patterns. Because we are making things as simple as possible, we want algebraic patterns! A pattern is simpler than listing all the numbers in it. At home: find ways algebra helps us simplify pesky calculations. Celebrate simplicity.

You might have noticed that using the same rule as input-output (with inputs of 0, 1, 2, 3…) or recursively gives different results. This is the second stroke of genius. Kids accidentally produced nonlinear, exponential systems when they iterated multiplication. We now had examples in the group to make some nice comparisons between linear and nonlinear functions – the goal of the whole day.

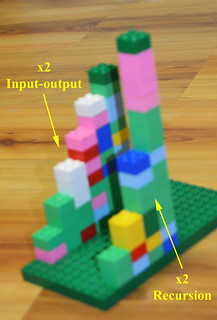
Why make things as simple as possible? Because you can deal with more complex things!

“But it is always straight if you only use two towers” – Stephen explains a property of a function, any function. We used straightedges to check if each set of towers was growing “straight like a slide” or “curvy like a roller coaster.” Children enjoyed making predictions, and then checking. If you only use two of the LEGO towers – whatever the overall pattern of towers! – you can always make a straight line between them. Drawing a straight line between two points on a curve is exactly what you do to find tangents, and to perform numeric integration, and in myriads of other calculus tasks. We will continue with this line of thought next time.

Video of the day –Sierpinski Dream