More math circles, multiplication, Math Future: Newsletter October 16
Subscribe and read archives
Pinterest | Twitter | Facebook | Google+
Hi, I am Moby and I bring you the news about Natural Math. Send me your questions, comments, and stories of math adventures at moby@moebiusnoodles.com

In this newsletter:
- More math circles for more kids!
- Easy and cute multiplication puzzles
- Live open Math Future event: Russian School of Mathematics (US Northeast and online enrichment)
Watch out for a BIG announcement tomorrow!
We’ve been very busy creating something really big and exciting! What is it? It is something many of you asked for over and over – an online course unlike anything we’ve offered before. Usually when you sign up for our courses, you receive plenty of ideas for math games and activities. In this course, you will learn how to create your own activities and how to lead your own math circles (and you will still get lots of ideas for math activities).
We wanted to make sure that everyone who enrolls in this course gets individual attention and support from us, so we limited the 8-week pilot program to 20 participants. We will send a separate e-mail with all the details of the course (including an early-bird registration offer) at 10am EST on Friday, October 17th. Don’t miss it!
Who leads math circles and why?

Anna Ignatov attended a math circle as a child, and then, as a mom, organized two circles for her two daughters and their friends. Since 14, Anna’s daughter Ida has been organizing math circles of her own: the third generation of circles, and counting! Why do they continue this tradition?
As Ida told us:
In school, we are taught that math is something boring, that we have to learn for some strange reason: you will need it in the future. Yeah, sure… It is nice to show the kids the beauty of math before they will learn once and forever that math is boring.
Read the entire interview with Anna and Ida in our 1001 Circles series and try a combinatorics game Anna and Ida shared with us.
Play this cute and easy multiplication puzzle with your kids
The new puzzle game Bojagi by David Radcliffe, which we review on the blog, is all about drawing areas. The rules are easy to learn, but Bojagi puzzles themselves are can be tricky to solve. Draw a rectangle around each number by clicking and dragging with a mouse. Each rectangle should contain exactly one number, and the area of the rectangle should be the same as the number it has. Rectangles must not overlap. That’s it!
Playful and gentle, this puzzle will help your kids see multiplication as more than just repeated addition. Take turns making puzzles for each other. Bojagi interface makes drawing designs, using algebraic formulas, or just playing with shapes easy. An online game, like Bojagi, that you and your child can play together is a great example of a new development in gaming called “intergenerational game design”. It is also one of the guiding principles we use in designing all Natural Math activities.
Speaking of multiplication games, come November we will once again be offering our most popular course, Natural Math Multiplication. We will announce the exact dates and registration details in our next e-mail.
Live open Math Future event: Russian School of Mathematics

On Wednesday, October 22 at 1 PM Eastern Inessa Rifkin, Irina Khavinson, and Nina Dubinsky will talk about the Russian School of Mathematics, one of the largest enrichment programs in the Northeastern US. Come and listen to a short presentation, chat with like-minded people from all over the world, and pose questions for the founders of RSM.
Register to join the event and get notified when we post the recording.
Math Future is an international network of people who care about mathematics education: researchers, developers, teachers, parents, and students. Since 2009, it has organized more than a hundred live online events with leaders of amazing projects.
Sharing
You are welcome to share this newsletter online or in print.
Talk to you soon! Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter
1001 Leaders – Ida and Anna on three generations of math circles: “Math is nice!”
Why would you decide to lead a math circle? Anna Ignatov attended a math circle as a child, and then, as a mom, organized two circles for her two daughters and their friends. Since 14, Anna’s daughter Ida has been organizing math circles of her own: the third generation of circles, and counting! Read Anna and Ida interview to see how their wishes for different mathematics as well as their happy childhood memories of math circles inspired them to organize their own circles.
Ida: When the kids are thinking, they suggest ideas that you would never expect.
In our 1001 Circles series, we feature math circles stories from the point of view of a circle leader, who acts a tour guide. In the companion series 1001 Leaders, we put the spotlight on the leaders themselves. What got them started and what keeps them going? What are their math dreams and worries? If you lead a math circle, an engineering club, or an informal playgroup, we would like to hear your story or interview you. Write moby@moebiusnoodles.com to talk about your adventures.


What brought you to math circles?
Anna: Since the age of 10 I was participating in math activities for kids. When my daughter Ida started school, I was looking for some activities to show her the beauty of math, but I couldn’t find anything that looked nice enough. So I invited Ida’s friends and we started this adventure. Our group kept going for six years, until the kids turned twelve, with five kids participating. Later I organized another group for Ida’s sister and her friends.
The idea was to show that there are not only instructions on “how to do math”, but also a place for thinking. I was also trying to find connections between math we learn at school and our real life.
Ida: When I was 14, I tried to repeat my mom’s experiment. I led a group of six-year-old children under my mother’s supervision. This group met for one year. Later, when I graduated school and started at the university, a boy I babysat since he was born went to school, so I created a group for him.
In school, we are taught that math is something boring, that we have to learn for some strange reason: you will need it in the future. Yeah, sure… It is nice to show the kids the beauty of math before they will learn once and forever that math is boring. Otherwise, their only chance to find out that math is nice is at the university, and only if they choose to study math. Another great thing is to see them thinking and enjoying it.

When the kids are thinking, they suggest ideas that you would never expect. For example, we checked different shapes for symmetry by building them with magnets, or by folding paper. Children came up with their own definition of a symmetric triangle: “Two identical edges, and the third one is even.” A child’s answer might be wrong, but the way of thinking is creative. Children become very happy when they feel that they caught the idea or found the reason for something.
Can our readers try one of your favorite activities from your math circle?
Ida: Once we decided to check how many different “chains” (sequences) of five objects we can make. We had two green stickers and three blue stickers. Everybody made a chain, and then we checked together if we already had that chain or not. Little kids don’t know combinatorics theory, but guess what? We eventually found 10 chains.

After that, we made a “tree” of those chains. You start with the two options, blue or green. Then you build “branches” and reason: to this branch, you can add blue or green, but to this one, you can only add green, because you ran out of blue… We counted the branches, marking them with stickers, and found out that there were – you don’t say – 10 branches! Making chains and making trees were two different activities. We discussed the connections only after we made the tree. Children liked discussing the connections. We didn’t attempt a rigorous proof that we found all the combinations, but we discussed why the tree shows us all of them.

It took us three meetings to explore and model the problem in depth. Children understood that there are 10 and no more chains, and were interested in discussions. We took breaks from the problem when kids got tired, did other activities, and then came back to the problem at the next meeting.
Anna: One very popular activity was “programming the robot.” To start, we decided together what we wanted our robot to do. We used a little doll (“the robot”) and a chess board. At first we just wanted our robot to arrive to the given corner cell, from any other cell. We had cards with commands, like GO, TURN RIGHT, and also conditional questions, like AM I AT THE EDGE? The algorithm was built from these cards. The task for the doll was to arrive from any cell on the board to the corner. One of the kids was looking only at the algorithm, giving orders to the robot and asking questions. All the other kids were moving the robot and answering questions. [This is an incredibly rich math circle task; check out a story in our 1001 Circles series about a similar activity, by DrTechniko – MariaD.]
The activity inspired discussions with kids. For example, they wondered how a robot knew when to stop. Could it see? Maybe it had some kind of a switch that turned the robot off when it touched the edge of the board?
Then we wanted to define some new robot – and one of the kids proposed to create a flight simulator. We never finished it (I wonder why!) – but we had very nice discussions of what it was supposed to do. We talked about maps and scales, and even tried to guide a robot-pilot through the map.
We returned to the robot game during several meetings. The nice thing is, the kids led the activity, bringing their own ideas of what they wanted to do.
Can you tell us about a difficulty you had when you led math circles?
Ida: One of the difficulties I had with the kids was to make them concentrate. Our circles started at 6 PM, we were tired by that time, and it was often very hard for the kids to get into the lesson. So I decided to begin the lessons with something very intriguing, to catch the kids right away. Then we moved on to the calmer main activities.
Anna: We had one our lesson every week. Sometimes we had to reschedule, or a kid missed a meeting. Young kids do not remember much after a week, let alone two. So, there was the feeling that we were not moving anywhere! I started to record what was happening and to post if online for parents. It helped parents to discuss our lessons at home. Kids could not always explain what we were doing. These posts really helped with our progress, because the parents took a more active part in our mathematics.
What advice can you give to newbie circle leaders?
Anna: The visual part of every lesson is very important. For example, it was a nice idea to build the robot algorithm with cards, rather than just saying the commands. We always used some objects to solve logical problems. We used toys for the classic river-crossing problem, “How can we take a wolf, a goat, and a cabbage in one small boat that can only carry one of them?” Without the toys, it was really hard for kids to follow.
Ida: Don’t expect fast results. Be prepared to return to the same idea again and again, from different points of view. Some day children will surprise you!
Posted in A Math Circle Journey, Grow
Bojagi: Cute multiplication puzzles by and for families
Multiplication is not just repeated addition, but what is it? From Montessori beads to algebra tiles, many developers claim the array and area models are great for growing children’s conceptual understanding and fluency in multiplication. You can go on scavenger hunts for the area model in tiles and bricks, and draw your own models using graph paper or computers.
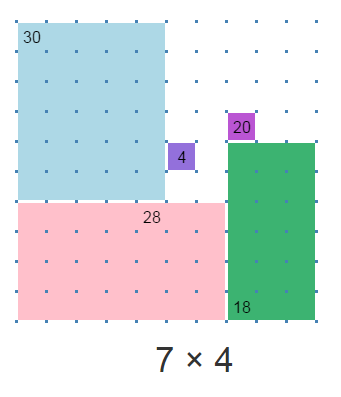
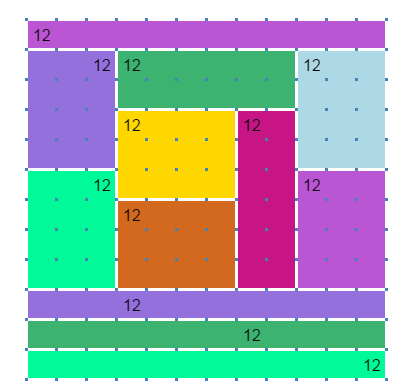
The new puzzle game Bojagi by David Radcliffe (@daveinstpaul) is all about drawing areas. Bojagi’s puzzles make you think, but the rules are easy. Draw a rectangle around each number by clicking and dragging with a mouse. Each rectangle should contain exactly one number, and the area of the rectangle should be the number that it contains. Rectangles must not overlap.
As you draw, the game tells you the two dimensions of your shape, for example, 7 x 4. If you break the rules, your shape disappears. The puzzles provide meditative fun for grown-ups and kids alike. The game helps kids learn multiplication in a gentle, playful manner. Making your own puzzles also feels great: you can draw designs, demonstrate algebraic formulas, or simply play with shapes in open-ended ways. A family or a math circle can take turns designing puzzles for one another.
You can find all the puzzles made so far in a big list, and add your own using the puzzle creator. Here are three quick puzzles I made when I first started playing:
- Not Squares has only square numbers, 4 and 9.
- The Fib is about the Fibonacci sequence.
- A Plus B Squared shows the four natural parts of the area that is 2+3 units by 2+3 units.

Bojagi demonstrates these design principles:
- Intrinsic learning. The area model of multiplication is the foundation of gameplay and tactics: you can’t make Bojagi without it. This is in contrast with extrinsic games, where computations are separate from the game mechanics (for example, correct answers let you explode monsters).
- Answer-first approach. You are given the result of the multiplication, rather than numbers to multiply. The task is to “reverse-engineer” the result.
- Strategic problem-solving. Not only do you need to find individual areas correctly, but these areas must also fit the whole puzzle. If they don’t, you have to retrace your steps and try the puzzle again. When solving good math problems, not only do you need to solve each step correctly, as in an exercise, but also to devise an overall strategy that works.
- Make your own math. The puzzle creator supports free play and open design of your own patterns.
Here is my interview with Bojagi’s creator, David Radcliffe.
 Please tell us a bit about yourself.
Please tell us a bit about yourself.
I am a college math instructor who is changing careers to software development. I graduated from the University of Wisconsin-Milwaukee with a Ph.D. in mathematics. I am interested in finding new ways to use software to help students learn mathematics, especially the tools that encourage exploration and creativity, not just memorization and skill development.
What is the motivation behind your game?
My game presents multiplication in a meaningful context: the area model. I think that it will help students to memorize multiplication facts, but also to understand them visually. It was very important to me that students should be able to create their own levels and share them with their friends, because I want to encourage exploration and play.
Many people say the area model is their favorite model of multiplication. What about you?
The area model is my favorite model of multiplication because it is so easy to visualize. The area model makes many of the properties of multiplication clear, such as the commutative and distributive properties. One weakness of the area model is that it is difficult to interpret multiplication with negative numbers using this model. In that case, I prefer to describe multiplication as scaling.
Your game has a lot of bridges to ideas. Can you name a few?
Besides practicing multiplication facts, the game can be used to explore factorization, divisibility, and prime and composite numbers. A child playing this game can discover that prime numbers can be covered by only one kind of rectangle. Kids may be led to ask which numbers can be covered by two kinds of rectangles. This line of investigation quickly leads to some very interesting concepts in number theory.

(This is a screenshot I took while making a puzzle that can lead someone to explore different ways to factor the same number – MariaD)
Anything else you would like to add, David?
I am a fan of your work with Moebius Noodles, so I am very happy that you are interested in my game. I would be glad to answer any questions that you have. Also, if you have any great ideas for games that I could implement, please pass them along.
Please leave questions and game ideas for David in the comments!
PLAY BOJAGI
Posted in Make
Fractal BugFest, future of learning, math storytelling: Newsletter October 6, 2014
Subscribe and read archives
Pinterest | Twitter | Facebook | Google+
Hi, I am Moby and I bring you the news about Natural Math. Send me your questions, comments, and stories of math adventures at moby@moebiusnoodles.com

In this newsletter:
- Math coloring pages and other activities to try
- Math Future live online meetings for teachers, parents, and teens
- Math Storytelling Day stories
Math coloring pages and other activities to try

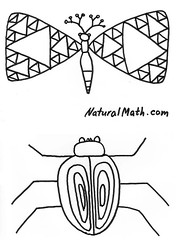
BugFest is a big annual celebration of insects and crustaceans at the North Carolina Museum of Natural Sciences, attracting some 35,000 visitors to its hands-on learning centers – for example, to explore fractals in nature at our table. We miss you already, BugFest friends, and hope to see you again next year! Huge thanks go to the amazing kids who liked our activities so much that they taught them to others. The two most popular activities at the BugFest were insect-themed coloring pages and origami.

The youngest math explorers and people of all ages who like art can color the Sierpinski butterfly and the Droste beetle, named after the fractal designs on their wings. Or you can design your own fractal fantasy creatures, as visitors did at our table.

Kids develop their intuitions of exponents and infinity with these easy but complex designs. Click to print a larger picture:
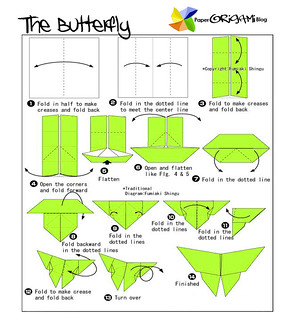
Some visitors wanted to go beyond the flat, 2-dimensional drawings – 1.58-dimensional, to be more precise, in the case of that Sierpinski butterfly. We invited them to fold origami butterflies. As a craft, origami develops several precious mathematical practices directly useful for geometric construction, topology, integration, and analysis of functions – and indirectly for all of math:
- Making shapes out of shapes, and seeing shapes within shapes
- Precision and accuracy
- Reasoning between flat, 2-dimensional medium (paper) and 3-dimensional shapes made out of it
- Decoding words, symbols, and visuals from directions into the kinesthetic experience of folding

Here are origami symbol and video instructions similar to the butterflies we folded. We skipped shaping the wings at the end (step 10) to make folding easier for the little fingers. Simplifying other people’s patterns is an easy way to start remixing your own origami designs.
This year, FIRST LEGO League world class challenge is, “What is the future of learning?” Two local teams invited Maria Droujkova to talk with them about learning – and once again, she invited kids to fold paper, airplanes this time. The first fold of the paper, just in half, can be explained with just words. As you build the airplane and the folds get more difficult, you have to show the folds, not just tell about them. Toward the very end, you must add the kinesthetic mode of learning to words and visuals. You and your student hold the project together; you guide the folds, so your student can feel how the fold must go. The future of learning is in making your own math – and in using all your senses as you do so.

We also came to a playdate with a local parent group called Wee Play. We met the kids and parents at a park, did a Math Trek scavenger hunt, drew some fractals, and made mandalas out of found materials.

All these activities help to grow your math eyes so you notice mathematics everywhere you go. If you’d like to try a Math Trek, choose a place you like and look for the items listed on the Trek Clue Card (click to get the PDF with 4 copies). Once you find the item, don’t forget to take a picture. You can always share the pictures with us via e-mail, on your blog mentioning Natural Math, or by tagging @NaturalMath on Twitter.
Another big September event was SparkCON, where Maria Droujkova presented a PechaKucha talk called 5 Year Olds Can Learn Calculus. It is a sign of a good connection with the audience when people come up to Maria afterwards and share their math stories – often grief stories: “Let me tell you what happened to me in the third grade!” You can watch the (homemade) video of the talk or look at the slides and the text.
If you would like to invite the Natural Math crew for your events, big or small, write moby@moebiusnoodles.com
For teachers, parents, and teens: Math Future live online events
Math Future is an international network of people who care about mathematics education: researchers, developers, teachers, parents, and students. Since 2009, we have organized more than a hundred live online events with leaders of amazing projects.
On Monday, October 6, at 1 PM Eastern Time, Dr. Keith Still of SaferCrowds.com will introduce his Crowd Sciences work. Learn more and register.
On Wednesday, November 5, at noon Eastern Time, Dr. Joseph Mazur will talk about his new book, Enlightening Symbols. Learn more and register.
Come and listen to short presentations, chat with like-minded people in the audience, and pose questions for presenters!
Math Storytelling Day stories
September 25 was the Math Storytelling Day – thank you for all the stories you sent! Check out these people and groups who joined the fun.
- The Hospital Floor. Denise Gaskins the brave, of Let’s Play Math, shares her thoughts about a semi-random tile wall in her hospital room where she landed with appendicitis.
- Crafting Stories is Juliana Lee’s blog about, well, stories, and she celebrates by reviewing three excellent children’s math readers.
- Bradenton Herald, a Florida newspaper, included Math Storytelling Day in an article by Stephanie Katz about absurd observances, in the excellent company of Talk Like A Pirate Day, our second-favorite September holiday. Arrr! (The official Pirate language page says it means “I am happy.”)
- The Upside Down Triangle author thinks Math Storytelling Day is the best holiday of the year – and posts one of my favorite animated math stories ever, The Cyberchase, to celebrate.
- 4 The Love of Math, a very prettily patterned, pastel-colored blog of Randi Loveland, posts a mini-guide to nerd t-shirts, so you can celebrate in style.
- Awkward Silence Comedy had an improv event staged, described thus: “ASC rides a Mobius strip to the moon! It’s Math Storytelling Day and you know what that means! Bust out those anecdotes about infinite hotels, sketch out some knots, remember that time that grandma forgot to carry the 1. Good times with Grandma, indeed.”
- Math Road Trip Project is a homework assignment that structures a math story around a road trip. How many calculations can you include before your story turns into a non-magical pumpkin, that is, a story problem? Try it and find out!
- Sequence Story Competition was held at Furness Academy, Cumbria, UK. Their intro video has several prompts for writing stories.
This week, we are producing and sending the official Math Maker t-shirts for everybody who ordered or won them. Don’t wait for Math Storytelling Day 2015 to share your story. You can send us a tale of your math adventures any day of the year!
Sharing
You are welcome to share this newsletter online or in print.
Talk to you soon! Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter