Snowflakes, Part II: 3D origami, fractals in the Alps, artistic apps
Subscribe to the Moebius Noodles newsletter
Welcome to adventurous math for the playground crowd! I am Moby Snoodles, and I love to hear from you at moby@moebiusnoodles.com
Special snowflakes, take 2!
Happy holidays! Last December, we wrote about snowflake-related math in our December newsletter. “Special Snowflake” is one of the most popular activities in the Moebius Noodles book (see below) and our workshops, so we are doing a snowflake newsletter again!
Snowflakes as fractals
What do snowflakes, trees, corals, and your lungs have in common? They consist of branching structures! These types of structures are called tree fractals. Check out instructions on how to make a hexagon-based fractal snowflakes designed by MathRecreation. You can make some snowflake tree fractals – or maybe tree tree fractals – as holiday decorations.
3D origami snowflakes
Most people know how to cut snowflakes out of paper. The Japanese term for paper craft with scissors is kirigami. But you can also make snowflakes in the tradition of origami, that is, folding without cutting. Just follow video instructions from Origami Maniacs. Origami is an art, but also a type of geometry, with its own set of axioms more powerful than Euclid’s. And as far as young kids are concerned, paper folding develops attention, precision, and appreciation of beauty: the values necessary for doing mathematics.
Giant snowflakes in the Alps… or at the beach
Check out giant snowflake art pieces covering whole mountain slopes. Even if you are not joining Simon Beck’s math adventures in the French Alps, you can make smaller symmetrical designs at the park or in your yard.
Snow is not an option? Make snowflake art at the sandy beach or in a sandbox!
Snowflake lapware
Lapware is the software for the kid cuddling in your lap. Here are my picks that show both beauty and symmetry of snowflakes.
Weave Silk feels great on touch screens (Android, iOS), but you can also play it on PC. The interface is easy enough for toddlers, and includes terms like 6-fold symmetry for parents.
Make sure to click both 2D and 3D rotate buttons after designing a snowflake with zefrank’s browser applet. The transformations are mesmerizing!
SymmetriSketch software for Mac, Windows or Linux comes from EvilMadScientist.com – with the name like that, it must be awesome!
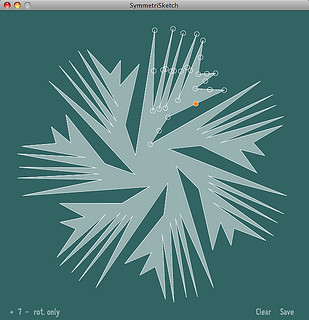
Sharing
You are welcome to share, remix and tweak. Please credit MoebiusNoodles.com under the Creative Commons Attribution-NonCommercial-ShareAlike license: CC BY-NC-SA.
Happy Holidays!
Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter
Purple Comet! math meet: 4 awesome design features, and a book
Many math symbols are really pictures, such as 0 for emptiness or ∞ for endlessness. In the title Purple Comet! Math Meet the exclamation mark in the middle is the picture of a comet, of course. But what is a math meet?
Pictures: the Buddhist symbol of emptiness, the infinity logo of the Journal of Humanistic Mathematics, and the Purple Comet! logo.
Imagine a group of kids who like to solve math problems, and who get together for the purpose. This is one of traditional ways to run a Math Circle. You just need some enthusiastic, more experienced kids or grown-ups as helpers, and good problem collections. Right? Not exactly! Turns out that in a few months, just solving problems becomes too monotonous.
Let us look at gaming. All successful games have a series of doable, satisfying, repeatable tasks. But these tasks build up to larger, more complex goals. Good games have sophisticated end-level puzzles, big construction projects that take all your resources, or fierce boss fights you can only win by heroic measures. You valorize the daily tasks, because you anticipate and remember these awesome special events.
The traditional big events for problem-solving Math Circles are math competitions. There are many competitions, but Purple Comet! math meet stands out because of its clever, modern design. As other quality competitions, Purple Comet! offers children original, meaningful, interesting, tricky problems that are a joy to solve – that is, real mathematics. But there is more:
- Global network, local communities. Purple Comet! is an international festival and an online event – but it consists of local experiences with friends. The global network generates energy, problem-posing support, and the sense of scale that a local circle would not achieve alone. But local communities provide the depth of discussion, camaraderie and nurturing that a global network lacks. Together, the two aspects work their magic.
- Teamwork. The vast majority of math and science is done collaboratively, but children often take tests and competitions alone. Purple Comet! invites teams to solve problems together, only competing against other teams. This allows for more interesting types of problems. For example, some problems require insight, which is more likely to happen in group brainstorming. Other problems split into multiple sub-problems, so each person can tackle a piece of the bigger puzzle.
- Technology is welcome. While doing things by hand can be artistic, quaint, or cute, most children who love science and math, and of course all STEM professionals, use computational tools in their problem-solving. Purple Comet! problems are designed with computing devices in mind. The problems focus on ingenuity and reasoning, rather than memory or computation. However, many problems are based on number patterns, so students learn to appreciate how numeracy and computational fluency help in problem-solving.
- Self-checking. The design principle of self-checking goes back to Montessori. All problems have nonnegative integer answers. At the beginning, this principle made it easier to program Purple Comet! software. By now, it became an appreciated tradition. If a team gets a different sort of answer, they know to rework the problem. The known format of an answer is a hint, but not a big reveal, like knowing the correct answer would be.
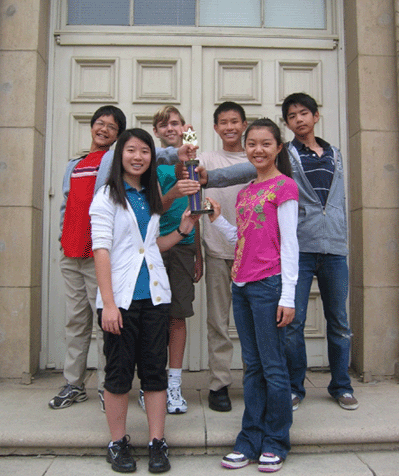
Photo: Pasadena Middle School Purple Comet! team
To share the joy, Titu Andreescu and Jonathan Kane of the appropriately named AwesomeMath assembled problems from the first ten years of Purple Comet! math meet in a hardcover book with beautiful, clean layout of formulas and diagrams. You can use the book as a source of problems for family math or Math Circles. If you are a designer, the collection will be a valuable source of strong practices in curriculum development centered on problem-solving.
This December, Purple Comet! and other books from AwesomeMath are 20% off.
Posted in Grow
Do your kids draw grids? Part II: shape-filling grids
Want to participate in citizen science, collecting data of children’s math art? Happy to display your child’s creations beyond your the fridge? Then send us grid drawings!
Thank you, Alexia Idoura, Maria Genkin, and Dan White for sharing your children’s art and stories.
Here is Part I of “Do your little kids draw grids?” And here is the fresh grid art, with a few comments on the psychology of math ed.
Alexia Idoura: This is one of Maxime’s grids from preschool – still have on my bulletin board!
Filling shapes with girds is more challenging than it looks. Notice how Maxime decided to continue grid lines from the edges of fingers to the edge of the thumb, rather than to the wrist? This allowed her to make the lines across, and still fill the space of the palm. She also changed the spacing and direction of the lines on the palm, but not on the fingers – because she was very aware of the boundaries! To make it work, it took a pretty sophisticated analysis of the shapes. Some five years later, Maxime is still doing grid art, rocking fractals at our Inspired by Calculus Math circle.
Here are two related grown-up art projects. David Chelsea‘s curvilinear perspective fill spheres:
Escher nested grids, also called Droste Effect fractals, fill curved spaces:
Maria Genkin gave me permission to post her son Ronik’s art. In Maria’s blog post with the pictures, she laments that young kids are pressured to adopt a primitive visual language of representational art, like stick figures and square houses with triangular roofs. I hope our collections of grids will help parents value and appreciate kids as abstract artists.
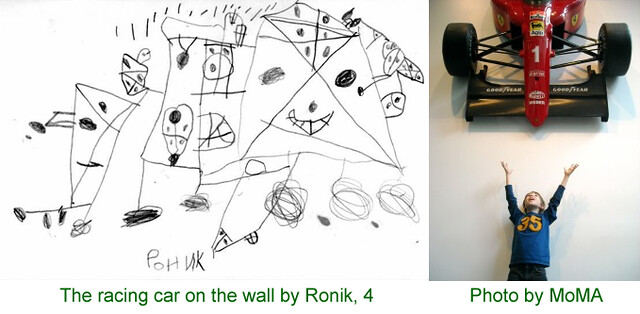
Note how Ronik uses different criss-crossing patterns to fill different shapes: the heart, the smile, kite-like forms. Check out the nested (fractal) element at the top of the “face” of the car. The square is separated by the diagonals, then the topmost triangle is separated some more. This grid within grid is an advanced stage in children’s grid art.
Here is another picture by Ronik, turning concentric circles into a grid. Before they learn to draw grids, children draw spirals or circles, by moving their hands around and around. They sometimes learn to do so before their first birthdays, but typically between two and three years of age. Even older kids often start an art project with concentric circles, and then turn it into a spiderweb grid.
Dan White says his daughter Addie (5) has been drawing grids for a while, more and more as she’s growing older. Addie often fills shapes with a variety of grid-like, regular textures, including parallel lines, zigzags, rows and columns of circles, and square grids. The creative math/artistic puzzle or problem with each of these grids is, “Which texture goes well with each shape?” You can see a curious stage of cognitive development in the top right corner of the picture above. Note how Addie (almost 3) drew a grid cell by cell by cell, rather than making longer lines cross. Some of the cells line up, but mostly they do not. In the bigger picture on the left, Addie (almost 4) drew some grids by crossing long lines, and some by arranging individual cells – this time, lined up much more. In this picture, Addie can line up cells by hand, because she now has a stronger image of grids in her mind.
Above is the illustration of the cell-by-cell grids from Moebius Noodles: Adventurous Math for the Playground Crowd. It comes from the chapter about doodle games parents and kids can play with grids.
In this more recent picture, Addie superimposed diagonals (which form triangles) over a square grid. That is, she built the new structure right over the old structure already in place. That is somewhat difficult, like speaking over another speaker. It requires pretty reliable mental images of the grid structures.
Posted in Make
Mood-o-meter, 0/0 yin-yang, books with friends: Newsletter December 2
Got this from a friend? Reading online? Subscribe! I am Moby Snoodles, and this is my newsletter. Send me your requests, questions and comments at moby@moebiusnoodles.com 
Questions and answers
Help @remypoon at the Ask and Tell hub with this new question:
How can we help young students to know learning mathematics is more than just getting the answer? Click to reply.
Sheryl Morris emailed Moby:
Manipulatives don’t always help – they sometimes impede learning. How do you feel about manipulatives?
Moby:
Here are some examples of known issues with manipulatives.
- Kids are driven to distraction and totally free play, away from any math whatsoever.
- The manipulative only represents one aspect of an abstract idea, but kids are forever stuck with that aspect, because the manipulative is so memorable (e.g. multiplication as repeated addition).
- Kids don’t know where the analogy in the manipulative breaks down (e.g. that points aren’t really tiny dots). No manipulative can capture a math idea completely and absolutely right.
- Often manipulatives aren’t sustainable. They take a lot of time to make, or a lot of money to buy – while a kid only spends a few minutes using them.
I feel that the best use of manipulatives is for students to MAKE them!
Bright, Brave, Open Minds: an online course starts December 2
More than 70 participants registered for the open online course on problem-solving by Julia Brodsky. The goals of the course are to help parents and teachers preserve children’s divergent thinking, and to develop critical thinking and problem solving skills. The course is the last round of crowd-sourced feedback for the Creative Commons book Julia is writing. 
Blogs and networks
Try an easy math craft: two paper gears that make mood-o-meter smileys, from our Facebook friends at New Gottland. The table on the right is like a multiplication table… of moods!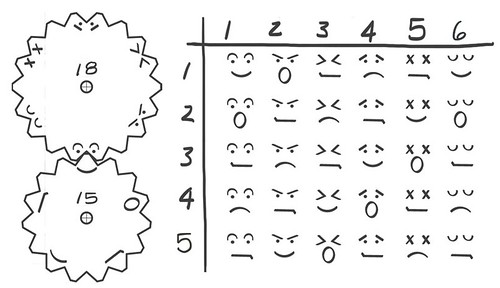 
When you need lapware (software for the kid is on your lap), try the PhotoSpiralysis nested fractal maker with your kids. My young guests and I had a lot of fun with it this Thanksgiving. 
Michel Paul discovered the zen of dividing zero by zero when he circled an expression on the blackboard. Loren Renee commented: “It’s a “pair of ducks” as my son used to say.” 
Yelena McManaman’s blog post “Fluency or complexity” sparked a discussion at our Facebook page. 
- Yelena: I am very proud of my 6-year old and the math discoveries he makes. Two days ago he came up with a proof that zero is an even number. Yesterday he built something he called “a square that has volume” (a cube), then connected 4 of them into a larger cube. And today, well before I had time to drink my morning tea, he shared his new discovery – turns out, Russian nesting dolls are fractal! I am very concerned about my 6-year old’s struggles with math. He still gets mixed up counting past 10. He is shaky with his math facts. He still needs to use fingers, counting bears or abacus a lot.
- Jeremy Vyska: I imagine it’s much the same way kids can do complex things like riding bicycles, climbing various playground equipment, etc; then have issues of tripping while walking. Practice will make the simpler things resolve/repair over time.
- Malke Rosenfeld: Most of the children I work with (upper elementary) do not yet have the skills they need to learn and perform complex percussive dance steps. I still wanted to give them a sense of what it feels like to dance in my art form, and also to create their own dance steps. How to do this without a lot of technique? I created Jump Patterns which allow children to think, create and communicate within the discipline. Their technical skills are developed on a parallel track.
- Kyle Griffin: Many of us who love chatting with our young children about the ideas of calculus and relativity and such still recognize an enormous gap between “ideas” and ability to do. I personally find that most of the time, one eventually hits a point with the ideas where the inability to do the thing results in an impenetrable barrier. That’s not to say that the idea-set isn’t fun, useful, interesting, and motivational. But it’s also nearly 100% independent of what other folks will care about in a child’s education. “I don’t care if you know the theory of good writing. Can you write well?”
- Peter Appelbaum: The misnomer that counting and arimethmetic is somehow fundamental to other kinds of mathematics really does lead to so many missed opportunities. Think if all of the successful mathematicians who are calculation-phobic. Of course, this is how ideology works. It masquerades as “reality.”
Book news: sharing with friends and math circles
Several people asked for easy ways to order Moebius Noodles: Adventurous Math for the Playground Crowd for a group of friends or a buyer coop. Now you get discounts if you order with a friend or three (2-4 copies), with your math circle (5-10 copies), or with a larger learning coop. You also save a lot on shipping. Happy holidays! 
Sharing
You are welcome to share the contents of this newsletter online or in print. You can also remix and tweak anything as you wish, as long as you share your creations on the same terms. Please credit MoebiusNoodles.com More formally, we distribute all Moebius Noodles content under the Creative Commons Attribution-NonCommercial-ShareAlike license: CC BY-NC-SA Talk to you again on December 15th! Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter
