Math like music
This story is a part of the ongoing conversation about children’s participation in math and the arts with Malke Rosenfeld of Math in Your Feet.
Photo by Kirsty Kelly
What if we could learn math like children learn music within a cultural tradition? What if we could learn math by being immersed in meaning and expression from the moment we’re born?
What does it look like when children fully participate in a culture as persons of recognized value?
Here children provide a high-energy improvised beat for a joyful street performance. The children are at the center of the action, and the adults smile as well as provide visual, gestural and verbal cues to encourage the children.
And here a little dancer’s performance is the heart of flamenco. It is obvious she is steeped in the music. We see the same kinds of encouragements as in the video above: warm smiles and supporting cues.
Alexandra Beller is following intuitive dances of a toddler to compose a profound interpretive piece, Milk Dreams. In our interview (coming up on this blog), Alexandra said:
“When I watch my company doing that material, I am totally transported. It’s a complete other world. I have never experienced anything like that. I can’t speak for a while. It’s a completely different space.”
Those teachers and parents who follow young children’s mathematics also describe how they feel transported to incredible, unexpected Wonderlands. While children take adults on adventures to the new frontiers, adults help to sustain connections to the homeworld. Kids and grown-ups make a great team, together.
Children in the first two videos perform music and dance at very high levels. But the third video shows the same mix of child inspiration and adult support with an obvious beginner: a baby! Children who have been supported that way from a very young age can do amazing music and dance. How do we build or find such a culture of participation and mentorship for children, so they are immersed in amazing mathematics?
Posted in Grow
How to Make Multiplication Tables with Perler Beads
My child has been playing with Perler beads for a while now making all sorts of things, including a map of Minecraft. So when I suggested making a multiplication table, the kid was very interested. Except a) I didn’t have a clear idea of how to make multiplication tables out of multi-colored beads and b) my child didn’t know what multiplication was.
No worries, I figured we would both learn by doing. Pretty soon we figured out that we wanted to use the large beads, not the little ones, and that making the entire tables would be too boring and time-consuming. So we decided to concentrate our efforts on square numbers.
After we put the cornerstone 1×1=1 round bead in the top left corner, the kid asked why do we call these square numbers if 1 didn’t look like a square. “Let’s make some more and see what happens, shall we?” Sure thing, 2×2=4 looked like a square and so did 3×3=9. But would 7×7 be a square? How do you know?
At first we made each square filled in with beads of the same color. So our 2×2 was all orange and 3×3 was all blue and 4×4 was all green and so on. It was pretty, but pretty boring. Then we started experimenting, taking out the inside beads so that only a square frame was left. So we decided to fill this frame with different colored beads. As we were discussing which colors to use for the 4×4 square, we noticed something:
2×2 square frame had no opening
3×3 square frame had a 1×1 opening
4×4 square frame had a 2×2 opening
What opening would a 5×5 frame have? Turns out:
5×5 square frame had a 3×3 opening, which had a 1×1 opening!
“Mom, it’s a fractal of square numbers!”
Let’s see what other patterns we noticed. Even squares (4×4, 6×6, 8×8 and 10×10) had even openings in them. And odd ones had odd openings. Why? Hint: it had a lot to do with the beads themselves and with how we chose to nestle the frames.
Then it was time to fuse the beads together and then to admire them. I set them out on a diagonal, as they would be in a 10×10 multiplication grid. The kid made another discovery of his own:
“We can integrate a pyramid with the squares!” and “This is like a mandala for Minecraft!”
My child played a very active role in the process, from choosing colors to noticing patterns to coming up with the unexpected connections to other ideas, like fractals and integration. What was my job? First, I helped keep the patterns consistent, especially when we did the frames. Second, I shared what I knew – the multiplication grid, square numbers. Third, I documented the experience. Later, as we looked through the pictures and went through my notes, it gave us both a chance to reflect on the math we found.
Together, we had a great time exploring and discovering patterns. Perhaps we’ll try the rest of the tables another time. Do you see bridges to even more ideas we can explore?
Posted in Make
Soroban abacus and finger math
Have you ever wondered why the Oriental Soroban abacus has 4 separate beads? It is in base 10, not 4 or 5, so why organize it that way?
In response to yesterday’s post Hand tricks! Alexander Bogomolny linked his page explaining finger math. As I looked at that neat way of counting to 99 on your two hands, I finally understood Soroban! The four beads stand for the four fingers on your hand, and the separate bead for the thumb.
With Alexander’s photos of hands, and screenshots from an online Soroban abacus, I can show the idea. It works the best if you count along. First, use the four fingers of your right hand to count 1, 2, 3, 4. This corresponds to the four beads in the first row of Soroban, shown yellow.
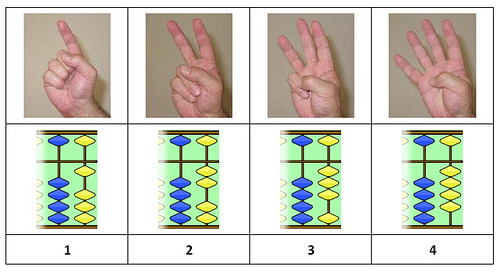
Then things become slightly more abstract. The thumb stands for 5, all by itself, just like the lonely yellow bead does. We move from direct counting to symbols:
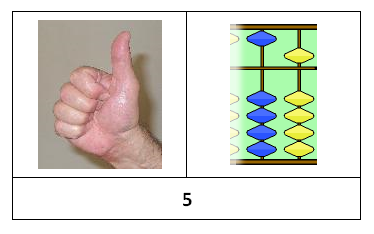
You add fingers to the thumb to count 6, 7, 8, 9. Imagine a young child playing traditional finger counting games with parents. Kids can instantly recognize (subitize) quantities from 1 to 4, but the Western finger counting goes all the way to 10 – well beyond the subitizing range. Unlike the Western finger counting, this system introduces groups and symbols (the thumb stands for 5), as well as addition, as soon as you leave the subitizing range. In other words, the system follows the way children’s minds work.
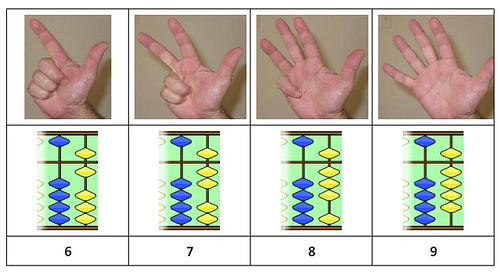
What happens when you arrive at 10? Something very rewarding and exciting! You get to use your other hand, which stands for the new place value – and the new row of beads on the abacus. The digits, the beads, and the fingers all fit together like hand in glove.
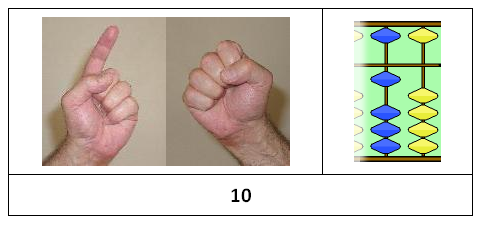
Here is another difference of this system from just counting your 10 fingers. You can count all the way to 99 on your two hands!
And if you join forces with a friend, you can show even bigger numbers.
Here is a video showing how to count all the way from 1 to 99:
Posted in Make
Hand Tricks!
Using one’s hands is practically intuitive in the math world. Counting on one’s fingers is the most basic mathematical practice one could think of. But there is other more complex math you and your kid can do with your hands!
For example, you are hardly limited to counting to 10. If you bring the binary system into the equation, your kid can count all the way to 1,023 using their hands. It’s pretty simple: 0 is your right fist, 1 is your right thumb, 2 is your right index finger, and 4 is your right middle finger. Do you see a pattern? Each finger number is the double of the one before it. So, if you want to count 6, you hold up your index and middle finger (2 and 4). A more thorough explanation is in comic form at Instructables.
In addition to counting on your hands, you can also use them as multiplication tables. Ms. K at Teacher Blog Spot explains how your kid can divide each finger into sections of 3 or 4 and multiply by the number of fingers, with a maximum of either 15 or 20.
A similar method of multiplying on your fingers is called finger reckoning. Finger reckoning has been used since at least the 15th century, when merchants would use it to calculate numbers out of the sight of competitors eyes. While Ms. K’s method is based primarily on counting, finger reckoning uses multiples of ten. It is more complex but you get the answer faster and more efficiently. You can read more about finger reckoning in our blog post about it.
There’s no need to limit you or your kid to computing multiplication and addition, however. An easy and useful trick for remembering how many days are in each month is to count out the months on your knuckles and the spaces in between. Make sure to remember that each knuckle is 31 days and each space is 30 days, except February, which is 28 or 29.
Hand tricks aren’t limited to computation either. One of the most common practices in kid art is tracing hands for drawings, and that can be used to teach symmetry. While we didn’t come up with this particular example, the Moebius Noodles book has a symmetry game called Double Doodle Zoo which demonstrates how one shape (like the hands) can turn into another (the heart).
An easy three-dimensional example of a hand shape is getting a few people together and having them recreate a fibonacci spiral with their hands. This is a great example of shapes in math and how they can transcend two dimensions.
You can do even more geometry with your body than making a Fibonacci spiral with your hands. In this video, mathemetician James Tanton explains how to do the National Math Salute. Using knot theory, you create a simple knot with your hands and undo it. The hand salute also uses elements of topology: the study of insides and outsides, and the orientation of surfaces. It’s simple to watch, but it’s easy to do it wrong. See if you and your kid can figure it out!
Posted in Make
