Multiplication Towers
Check out activity ideas, adaptations by ages, and even more examples of Multiplication Towers (plus 14 other awesome topics):
Multiplication Explorers Self-Paced Course
One of the wonders of the ancient times is that many tribes and nations from different continents independently discovered and built patterns we call Labyrinths. Some math ideas are universal like that! Over the last decades, the Multiplication Tower idea has been appearing in many different projects. We interviewed authors from the 1970s to early 2000s, and it turned out they came up with the idea independently! But for the last few years, we’ve all been talking to one another, directly or through our blogs. Kids and their grown-ups build multiplication towers using many kinds of materials: wooden blocks, LEGO bricks, software and 3D printing, and beads.

This page documents the appearances of multiplication towers. If you build a tower or know of an example we missed, please send it to moby@moebiusnoodles.com
2013 Moebius Noodles
We have a chapter on Multiplication Tower games for young kids in the Adventurous Math for the Playground Crowd book. It summarizes ideas from many other projects on this page.
2013 Malke Rosenfeld
In a blog post with many quality photos and thoughts on commutativity, Malke shares her easy-to-make, beautiful version of the Tower.

Malke writes: “When we started building this tower the questions started flooding in. I started wondering about a LOT of things…” Indeed! So will you wonder, if you build the tower.
2013 Sarah Dees

In her blog post, Sarah included detailed instructions and her thought about the design. She writes: “The finished graph lends itself to interesting observations if you look at it from different angles. I ordered the blocks from the Pick-a-Brick section on lego.com. We have invented several math activities with these bricks (more posts to come!), and it has been totally worth the cost.” Sarah’s activity was inspired by Malke’s beads.
2013 jmommymom at Highhill Homeschool

What a creative way to replace materials! The blog post explains: “We didn’t have a foam block, so we filed a cardboard box with cotton to serve as our base. Then we stuck in wooden skewers in a 5×5 grid pattern, and added beads to that corresponded with the multiplication tables.” This activity was inspired by Malke’s beads, as well.
2013 Andrew Staroszik and Roman Hegglin on Thingiverse
In 2013, several tower model appeared on Thingiverse, a 3D printing site. You can use these files to print your own towers.

Andrew’s tower was originally inspired by Michael Punzak’s wooden model we describe below.

Roman’s tower comes with captions in Roman numerals and Braille. It’s also made of thin tiles rather than cubes. These two features make for more formal or abstract remixes.
2010 Brenda Weiss
Brenda is a physicist and a creative parent. When her son Corbin set out to make a multiplication table with Cuisenaire rods, he built the first set of towers on his own. Brenda writes: “In ‘helping’ make it symmetric, I ended up knocking over most of what he had built. We built this together. Corbin was responsible for the multiple block levels, as I couldn’t balance more than two blocks.” It helps kids to know they are giving real help. Take a page out of Brenda’s book: be open about the areas where you need help.

2010 Colin Graham
Colin made a collection of 20 math adventures with LEGO, modeled with the free Digital Designer software, and invited colleagues to add more ideas. Here is the multiplication tower from his collection.
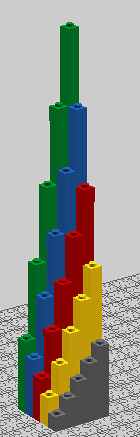
2007 Studio 1:1
The design studio from Gdansk, Poland made this giant tower and took several artistic photos of it.

2004 and up, Maria Droujkova’s Math Circles
Five Math Circle kids built these LEGO towers on a chessboard in 2010. The story was that each block was a creature (hence the smiley faces) that kept growing from row to row.

Later in 2010, the same Math Circle built a model with a cereal box and bamboo skewers. The picture shows the 3 by 4 array with pencils. The skewer in the lower right corner of the array sticks out by 12 units, that is, 3×4.

The above model was inspired by the Kinetic Structure BMW installation:
An earlier picture, from 2004, shows two kids from a Math Circle building with LEGO on a poster board.

2001 and up, Dor Abrahamson and friends
In 2010, Dor wrote: “Multiplication Tower as an Object-to-think-with.” Well put! Check out Dor’s page about 3d multiplication, with more pictures, at his Embodied Design site at University of California, Berkeley. This six-foot structure made of wood was constructed by Michael Bryant, one of Dor’s graduate students.


In 2005, when 3D printers were still rare, Paulo Blikstein printed this model at Uri Wilensky’s lab. Here is Dor playing with the Tower. Paulo now leads Transformative Learning Technology Lab at Stanford.

Here is a third grader building the multiplication tower from plastic blocks and play-dough in one of Dor’s experiments in 2001.

That was the year Dor designed the tower, first as a 3D output from a spreadsheet. Here is that historic document.

1988 and up, Michael Punzak, Michael Gleason, Douglas Shult, and Joshua Tenenbaum

Michael writes in commentary to his page of lovely hands-on explorations into patterns: “I made my first model about 20 years ago. It was inspired by an article and photograph in The Mathematics Teacher (Shult, and Tenenbaum, 1988: A three-dimensional multiplication table inspires mathematical discovery). I found this first model, which is about 3 feet tall, a lot of fun to paint (about 10 coats of acrylic, to get a metallic look to it) but very heavy to schlep around. I commissioned a friendly carpenter, Michael Gleason of Newton, MA, to build a smaller (about 18 inches tall) model, which is much lighter. I also use a 5-by-5 multiplication table model built with LEGO blocks for volume and surface area challenges. It is surprising and a bit disappointing that so far my 4-6 graders (a STEAM) after school class in Needham, MA, have not made the necessary jump from the 5×5 model to the 10×10 model.”
1975 Don Cohen
In the oldest multiplication tower we found, the layers were cut out of wooden Dienes blocks by Don. He has kept it around for his students to build up the layers and to find more patterns. His camera wasn’t good at close shots, so the numbers here are written over the picture. Check out Don’s work on calculus by and for young people!

Happy tower building!
Posted in Grow
Beautiful Objects
Note: This post originally appeared on my personal blog on January 24, 2014 and can be found here. At the end of this post you will find a question related to the following story–I would love to hear your thoughts, ideas and responses. –Malke
___________________________
I’ve been thinking quite a lot lately about the role of physical objects in math education. Sometimes called manipulatives or, more generally, tools, I’ve discovered conflicting opinions and strategies around the use of such objects. In her book Young Children Reinvent Arithmetic, Constance Kamii helpfully sums up some of the issues with which I’ve been wrestling:
“Manipulatives are thus not useful or useless in themselves. Their utility depends on the relationships children can make…” p25
“Base-10 blocks and Unifix cubes are used on the assumption that they represent or embody the ‘ones,’ ‘tens,’ ‘hundreds,’ and so on. According to Piaget, however, objects, pictures and words do not represent. Representing is an action, and people can represent objects and ideas,but objects, pictures, and words cannot.” p31
So, it is not the object itself that holds the math, but rather the process in which the learner uses the tool that creates the meaning. But, of course, when we use this kind of language we are talking abstractly about hypothetical objects and generalized characteristics of ‘the child,’ not any specific object or individual learner in particular.
Too much generality and abstraction drives me crazy so imagine how pleasantly surprised I was when this showed up in my mailbox the other day:

What is it? Well…it’s an object. And a beautiful one, at that. An object that can be “manipulated” (the triangle comes out and can be turned). A thinking tool. It was designed and created by Christopher Danielson to investigate symmetry and group theory with his college students. Not only are parts of this tool moveable, but it also has the potential to help “facilitate [mathematical] conversations that might otherwise be impossible.” (Christopher on Twitter, Jan 17, 2014)
What was even better than getting a surprise package in my real life mailbox containing a real life manipulative (not a theoretical one) was my (real) eight year old’s interest in and reactions to said object.
She spotted the envelope and said, “Hey! What’s that?!” I told her that a math teacher friend of mine had sent me something he made for his students to use. I took it out of the envelope for her to look at.
First thing she noticed was the smell — lovely, smokey wood smell which we both loved. She investigated the burned edges, tried to draw with them (sort of like charcoal). This led to a discussion about laser cutters (heat, precision) and the fact Christopher had designed it.
I pointed out the labeled vertices on the triangle, showed her how you can turn it, and mentioned that the labels help us keep track of how far the shape has turned. She immediately took over this process.
She repeatedly asked if she could take it to school! I asked her, “What would you do with it?” She said, matter-of-factly: “Play around with the triangle…and discover new galaxies.”

Then, she turned the triangle 60° and said, “And make a Jewish star…” Then she put the triangle behind the the opening so it (sort of) made a hexagon. I asked, “What did you make there?” She said, “A diaper.” Ha!
I hope Christopher’s students are just as curious about and enthralled with the “object-ness” of this gorgeous thing as they are with the idea that it helped them talk and think about things that might otherwise be impossible to grasp. I know that the objects themselves hold no mathematical meaning but watching how intrigued my daughter was with Christopher’s gift, I am left thinking about what we miss out on if we consider a tool simply a bridge to the ‘real’ goal of mental abstraction.
Beautiful and intriguing objects, I think, have a role in inspiring the whole of us, all our senses, kinetics, and curiosities, not just our minds, to engage in the process of math learning. An object doesn’t necessarily have to be tangible; narrative contexts are highly motivating ‘tools’ when working with children. As I blend math, dance and basic art making I see over and over again how presenting the object (idea) first pulls my learners in — they are curious about what this dance is, how they might weave their own wonderful designs using math, what does she mean “growing triangles” and why are these pennies on the table?
Learning is hard work, but my experience is that students will gladly work hard if they have even a small sense of the direction in which they’re headed.
MALKE’S QUESTION:
MALKE’S QUESTION:
_____________________________
Malke Rosenfeld is a percussive dance teaching artist who blogs about her experiences at the intersection of math, the arts, and learning at The Map is Not the Territory.
Malke Rosenfeld is a percussive dance teaching artist who blogs about her experiences at the intersection of math, the arts, and learning at The Map is Not the Territory.
Posted in Grow
The Mirror Routine
If you have seen any comedic performance in the past century, you have likely seen the Mirror Routine. When two people try to seamlessly imitate each other, it is not only entertaining to the viewers, but to the performers as well!
In its chapter on symmetry, the Moebius Noodles book gives instructions on how to do this “live mirror” activity with your kids, with examples of movements, and extensions of the game. The Mirror Routine is easy to learn for both kids and adults when the movements are simple. As they grow more complex, however, you may find yourself struggling to keep up with your kid!
[youtube=http://www.youtube.com/watch?v=VKTT-sy0aLg&rel=0]
The Mirror Routine has been around since vaudeville days. The most well-known example of it is this scene from the Marx brothers’ film Duck Soup. In Duck Soup, Harpo Marx’s character breaks a mirror and pretends to be his brother’s reflection in order to conceal it.
[youtube=http://www.youtube.com/watch?v=E4YZKGpe-D0&rel=0]
Twenty-two years later, Harpo Marx returned to the screen on I Love Lucy. When Lucy tries to trick her friend Carolyn into thinking she is Harpo Marx, she is surprised by the real Harpo and mirrors his exact movements.
Your kid or student might be familiar with the routine already! In this scene from My Little Pony: Friendship is Magic, pegasus Rainbow Dash is confronted with a changeling clone of herself and mirrors her every move.
[youtube=http://www.youtube.com/watch?v=64bAg3Zz40w&rel=0]
Or, if your kid is a fan of Adventure Time, they might have seen the magical dog Jake attempting and failing to do the Mirror Routine when his human friend Finn catches him trespassing in their friend Marceline’s house.
Invite your kids to try the Mirror Routine: it will challenge and delight the little performers.
Posted in Make
Math Cafe, holidays <3, three new book and course projects: Newsletter January 31
Got this from a friend? Subscribe!
I am Moby Snoodles, and this is my newsletter. Send me your requests, questions and comments at moby@moebiusnoodles.com

Math Cafe February 18
Several of us at Natural Math are long-time fans of Science Cafes. Yelena McManaman and I presented a Cafe on early cognition in 2013, and will present a teen Cafe on math-rich occupations in March 2014, at the North Carolina Museum of Natural Sciences. From their definition of Science Cafes:
Anyone can participate in topical discussions with leaders in the fields of science and technology. These talks promote discussion of science in an informal setting. Prominent researchers share their expertise during presentations, discussions, and informal talks.

We want to organize a series of cafes of our own: Math Cafes, open to the world. If you are in the Raleigh-Durham area, NC, join Yelena and me on February 18th at 6 pm EST at Cafe Carolina on 137 Weston Parkway, Cary. Bring a device to participate in text chat. If you are elsewhere, brew a cup, get a cookie, and join us online. Get together with friends and family for your own local chat, if they can join you. We will do a short sweet presentation on the surprising and wild science behind multiplication. Then we’ll answer questions from online and local participants – while you informally discuss the ideas. After we try out the format, we will be bringing other leaders of mathematics education communities for more Cafes.
Registration is free and open: your entry ticket is a question about multiplication. Register now!
Description of the first Math Cafe: What is multiplication?
What is multiplication? Well, it’s when you multiply one number by another number. Hmm, that doesn’t sound very helpful, does it? What does it mean to multiply a number by another number? Your child’s experience with multiplication will depend on the answer (or several) you have to this question. It will also determine where you will look for examples of multiplication – multiplication tables, a mirror, your child’s drawings, a stroll around your neighborhood… And researchers suspect that early experiences with multiplication (or lack thereof) largely determine the future success with all math and science. That’s because multiplication is the cornerstone of algebra.
How will learning these critical concepts fit your and your child’s day-to-day activities? And how will it help enrich your and your child’s relationship with mathematics? We will discuss these and other questions in our upcoming Math Cafe.
It is open for sign-up now. Even if you can’t attend, sign up anyway, and we will send you the recording. Ask us your question, tell us your or your child’s multiplication story, share your successes or concerns. The power to shape you child’s view of mathematics is in your hands – and it all starts with asking questions!
(Math) x (Holidays) = <3
February 7th is e day. It’s less famous than the Pi Day, but the more math holidays, the merrier! Check out an intuitive guide to e from Better Explained.
If you want to bring math into Valentine’s Day, here is a cute heart-shaped card idea from KrokoTak, similar to the Moebius Noodles art and visualization game called “Double Doodle Zoo.” Check out the clever use of symmetry and negative space!

Book news
With help from Polgarus Studio, we are making a simplified layout of Moebius Noodles for ebook readers such as Kindle, and also for the translations.Our colleague M. Onur Cesur, a professor at Maltepe University in Istanbul, is going to lead the Turkish translation. The closest to completion is Hebrew; Russian and Farsi are done. If you are interested in translating the book into another language, let me know.
There is also good news from Delta Stream Writers, a Natural Math incubator for projects similar to Moebius Noodles. We just began three new projects, which means more online courses for you, and more books – very soon!
Rodi Steinig of Talking Stick learning center, a math mom, and a blogger is working on a book about her Math Circles – with big help from her daughter Rachel.

Photo from Talking Stick.
Mark Saul and Sian Zelbo of Center for Mathematical Talent, an outreach program of the Courant Institute of Mathematical Sciences, New York University, are making a book of logic games and activities for Math Circles.
Kalid Azad of Better Explained will be joining Yelena McManaman and me in turning our Inspired by Calculus adventures into a book.
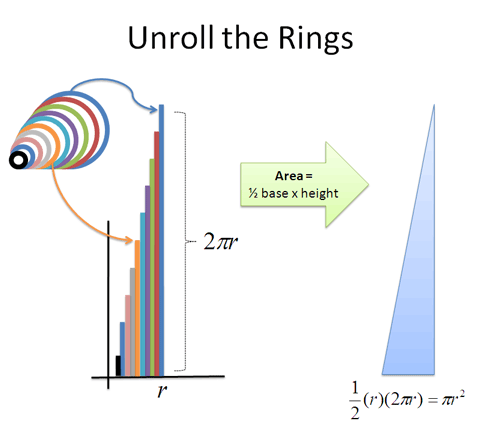
Picture from Kalid’s Gentle Intro to Calculus.
Sharing
You are welcome to share the contents of this newsletter online or in print.
Talk to you in two weeks! Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter










