Multiplication: A parlor finger trick
Click numbers on the left and on the right to set up an example:
This Flash applet teaches you how to compute times tables from 6 to 10, on your fingers. The trick was first recorded around 15th century, when merchants collected techniques called finger reckoning to calculate their profits. Back then, calculating devices were bulky. But you can do finger reckoning under the table or in your pocket, away from prying eyes of competitors. Now we do finger reckoning for fun.

Instructions in words
Number your fingers, starting from 6 on thumbs. You may want to write numbers on your nails.
- thumbs 6
- index 7
- middle 8
- ring 9
- pinkies 10
Bring together the fingers with the numbers you are multiplying, for example, index (7) and middle (8) for 7*8. The fingers that touch, and any fingers under, count as tens, so you get 50 in this case. Multiply the other fingers, left and right, in this case 3*2=6. So you get 56 as the total, which is the answer to 7*8.
Why does it always work? Here is a formal algebraic proof…
Suppose you multiply numbers A and B on your fingers. The trick tells you to count this many tens on either hand: (A-5) + (B-5) as your tens. And your ones are (10-A)*(10-B).
The total is:
(A-5+B-5)*10+(10-A)*(10-B)=
10A+10B-100+100-10A-10B+AB=
AB
But I bet this isn’t how did the merchants of old came up with the system! Was it something about their counting boards or abacuses that suggested the finger trick?
Do you know a plausible explanation about the origins of this trick?
Posted in Grow
Topo maps, musical fractals, easy and complex tasks: Newsletter April 18 2014
Subscribe to Moebius Noodles newsletters
Pinterest | Twitter | Facebook | Google+
I am Moby Snoodles, and this is my newsletter. Send me your questions, comments, and stories of math adventures at moby@moebiusnoodles.com

Seeking all video makers!
We are starting to build Mathematician badge for the wonderful DIY.org site. We need short videos showing how to make things rich in math, mostly models. If you want to collaborate, drop me a line!
Math Spark: Topo maps and derivatives

Can you match mountains to their topographic maps? This mini-game has to do with the idea of slope, which is one of the less steep paths to the idea of derivative.
What happens to the slope when the level lines on the map get closer together? Are higher mountains always steeper? For these and other questions, read the story from our local Math Circle.
Have a math spark from your family or group? Email us so we can share your adventures on the blog!
News from the open Multiplication course
Our online course is in its second week. Participants share deep observations, thoughtful questions, triumphs in parenting, and lots of visual media. Here is a glimpse: James composed “Fractal Jacques” for his baby girl. He writes:
My daughter was in a fussy mood this morning, so we went with a music fractal, as music often makes her happier. We chose one of the songs from her music class, Frère Jacques. It’s 16 measures long, so we pulled out the middle 8, sped up the tune to double time, and inserted that in instead. The double time tune also has a middle (4 bars now), so we put in the original sped up 4 times. Finally, we put in two bars of 8x in the middle of that. We did try even faster, but it was too hard for me to spit out words that fast. Since Frère Jacques is a round, all the iterations can be played at the same time without getting too much clashing of harmonies. Here’s the sheet music for “Fractal Jacques”, followed by a video me singing the fourth iteration to my daughter along with a midi rendering.

Blogs and networks
Our Marina Mersenne interviewed Chiu-Ki Chan, the creator of Heart Collage, for our blog. Building objects out of smaller objects is one of the main ideas of calculus – in this case, embodied in photo collages.

At Bloke School blog, Dave Pommier totally gets the essence of the Moebius Noodles book:
I have seen quite a lot of people discussing moebius noodles, and have just recently managed to acquire a copy of their book. It is full of ideas which can be as simple or difficult as you are prepared to make them, which is what I enjoy about it most. It is a book of easy complexity.
Dave says that kids’ covariance grid got too whimsical when he left for work around Column 3, but I notice what I call local structured variation between some cells. It’s a precursor to grid reasoning!
In an instance of synchronicity, our Matt Droujkov uses a semiotic square to show how math activities can be easy and complex at once, like many of our Natural Math designs, or simple and hard at once, like a worksheet with a hundred of mundane exercises.
I will keynote the Learning Revolution online conference next week. My presentation is called From adventurous learning to disruptive innovations: brave design in mathematics education. I hope you can join! Here is the conference info.

Sharing
You are welcome to share the contents of this newsletter online or in print.
Talk to you soon! Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter
Inspired by Calculus Math Circle – Week 4
Even if five-year-olds can play with advanced ideas, can they do the next steps toward formal math? Can they actually integrate and differentiate? Are they capable of sufficient level of abstract thinking? These are the questions we are focusing on as our “Inspired by Calculus” local math circles for 7-11 year olds are getting closer to the end. Do try these activities at home by yourself (good), with your child (better), or invite some friends over (the best). If you do, please share your experience with us. As always, we welcome your questions and comments.
Week 1 activities | Week 2 activities | Week 3 activities
Week 4 – Islands, Mountains and Steps
The pre-circle homework this time was to match bird’s eye views of mountains with their profiles. The kids seemed to like it and felt inspired by it. They brought pictures of islands and mountains and showed us how different mountains from the homework can be modeled using one’s hands and arms. Maria shared a neat papercraft, a hyperbolic paraboloid. In case you want to make one, here’s how.
The show-and-tell helped us get started with the theme of the day – the relationship between slopes, and slices or layers. Maria showed the kids a rolled-up strip of foam. What will this circle look like if we push it through the center? The kids’ answers included a “round pyramid”, a cone, a hat, Pilot Mountain (a North Carolina landmark), and an upside down tornado. The kids showed not just their understanding of the idea, but also their ability to seek similarities between objects, an important step on the way to developing abstract thinking (more on this – later).
Next we asked the kids to become map-makers, to draw their fantasy islands and add contour lines. Some of the islands the children designed included a spoon island, a heart island, a fish island, and a rooster island!
Once the islands were designed, the kids got felt, craft foam, and decorator foam. They started tracing and cutting out the layers of their islands. There was confusion over what needed to be done. We did have a pre-assembled model to show, but forgot to do that step. Usually our maker activities are very open-ended. We do not have to show what the end result needs to look like. But this time the island-making was not an end in itself, but a bridge to the next activity. And it needed to be done just so.
What happens to your math circle if you mess up the plan? It’s a measure of the robustness of the group. In this case, perseverance (kids stayed on task) and cooperation (parents helped) kicked in and all the children ended up with great islands. You need soft skills like perseverance and cooperation for most STEM professions.
Once the islands were ready, it was time to explore their mathematical properties. We started with a “can you imagine” game of wild questions. Can you imagine a mountain with an infinite slope? An infinitely high mountain? A mountain with a zero slope?
It can be risky to start a discussion with questions about “extreme cases.” Kids might lose the main concept altogether. After all, most slopes are neither zero nor infinite. But by now kids had many encounters with the idea of a slope. So we felt safe. Still, the questions threw them for a loop and made them look for very divergent ways to satisfy these extreme conditions. Some laid their pieces down flat, jigsaw puzzle-like, modeling a zero slope, others set the pieces on edge on top of each other for infinite slope.
One of the children chose thin material (craft foam) for her heart mountain. Others opted for the chunkier decorators foam or a mix of materials. As the kids were building vertical slopes (infinite slopes), Maria pointed out the fact that even though the Heart Mountain was not high, it could still be arranged to show infinite slope.
This Heart Mountain provided a perfect bridge to the next activity. Maria modeled three slopes – a vertical one (holding up an index card), a steep-angled one (folding that right angle in half) and a shallow-angled one (folding in half again). She asked the kids to rearrange the layers of their islands to match these slopes. How can we show ever smaller slopes?
A couple of kids suggested decreasing the height of the mountain by removing a few layers or squishing the foam. The chunky models, most with only 3-4 layers, were not very helpful. The kids struggled to imagine a smooth mountain. They needed smoother models with more, and thinner, layers. Using 3×5 cards to “smooth out” the slopes helped somewhat.
Why was it so hard for the kids to understand that a slope does not have to change if the height of a mountain (or pyramid) changes? Size is absolute, but slope depends on the ratio of two sizes – so the size is “in there somewhere,” but indirectly. Slope is a relationship OF sizes, so it’s a derivative concept in more ways than one.
Can we train the kids, at this point, to do formal differentiation? We can train them to do some, for sure. But that would not be interesting, probably not developmentally appropriate, nor helpful to the kids in reaching their current life goals.
So why bother? Are we making a mountain (pun intended) out of a molehill when we call it “early calculus”? After all, calculus requires a great deal of abstraction and, as we just said ourselves, the kids aren’t there yet.
Noticing Similarities – Keys to Math Fluency
The goal of our math circles is to help children develop mathematical mastery. The part of mastery we focus on is not calculation, but the ability to recognize similarities and differences in ideas and abstractions.
During the Circle, children often describe something as something else. This week, for example, they described a shape as a silly hat or a “circle pyramid” or the Pilot Mountain. This shows us that they are developing their ability to move past superficial differences, to notice and celebrate similarities.
Noticing differences is an important skill, but it is also something we do well with very little practice. Noticing similarities is much harder, but it paves the way to abstract thinking. Introducing calculus concepts to young children helps them further develop this “similarities over differences” view. For more on the importance of noticing similarities, read this short Wiki entry .
The Inspired by Calculus series will wrap up next week when we post the notes from the math circle’s final meeting.
Posted in Grow
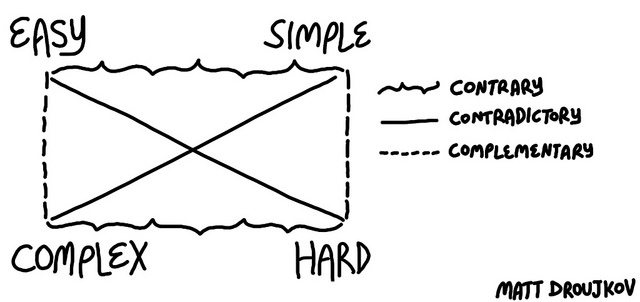
Semiotic Square: Easy-Complex-Simple-Hard

The semiotic square is a tool used for the structural analysis of relationships, developed by linguist Algirdas Greimas. We’re going to relate four different concepts in three different ways.
First we want to rule out the incompatibilities. The diagonal lines represent a contradictory relationship. Easy and hard live on opposite ends of one spectrum, so you can’t use them both in one sitting. Likewise, for something to be both complex and simple is a contradiction.
Next, the squiggly horizontal lines represent a contrary relationship. These are kind of like cousins. They might have similar properties, but they’re on different spectra, so they can coexist. When the stars align, something can be both easy and simple.
Lastly, the vertical connections represent a complementary relationship. This is a sort of double-negative. Complex is the anti-anti-easy. Simple is the anti-anti-hard.
If you want to go even further, you can add examples to your connections. My favorite way to do this is to embed the semiotic square in a rhombus, and label the points of the rhombus with examples that correspond to the connection. I think about pedagogy when I look at mine. The ideal activities are complex but easy, like building elaborate structures out of prefabricated LEGO blocks. Conversely, drilling long division in bulk is hard but simple.
I first came across the concept in Kim Stanley Robinson’s Red Mars. The diagram above is the very same one that appears in the book. Red Mars chronicles the history of the first one hundred colonists of the red planet, and their successors. One of the characters, a psychologist and an aspiring philosopher Michel Duval, is responsible for choosing the first hundred, and later for their well-being when he joins their ranks. Michel uses the semiotic square to classify the other Mars colonists, as an attempt to extrapolate from the traditional introvert-extrovert spectrum.
I loved it immediately for how human it is. Once you figure out the semiotic square, you’ll start seeing applications everywhere. If you make your own, share them in the comments. I’d love to see.
Posted in Make













