1001 Leaders: Make and fly boomerangs with Yutaka Nishiyama
Professor Yutaka Nishiyama(西山豊) seeks mathematics in everyday life and in cultural traditions. How does an egg roll down a slope? Why do French, Japanese, and Indian people count on their fingers in such different ways? Why do boomerangs fly? Yutaka finds out through research so playful you can follow it with your kids. I love how his accessible explorations mix childlike curiosity, the DIY spirit of making, the scientific experiments – and global sharing. In 1999-2007, The International Boomerang Project for world peace translated instructions for making simple paper boomerangs into 70 languages, making it accessible to 99.99% of the world’s population.

Photo: Yutaka Nishiyama with a variety of boomerangs, 1992
In our 1001 Circles series, we feature math circles stories from the point of view of a circle leader, who acts as an invisible tour guide. In the companion series 1001 Leaders, we put the spotlight on the leaders themselves. What got them started and what keeps them going? What are their math dreams and worries? If you lead a math circle, an engineering club, or an informal playgroup, we would like to hear your story or interview you. Write moby@moebiusnoodles.com to talk about your adventures. Here is the interview Prof. Yutaka Nishiyama gave for the series. When Yutaka works with kids and adults from all over the world, the activities center on simple curiosity about objects from the daily life. Try this technique with your kids!
How did you start working on mathematics? How did you get interested in topics such as boomerangs and direction of writing in different languages?
When I was young, I liked math – or rather, I needed math, like I needed eating. I studied math earlier than my friends did, and I was bored with math textbooks at school, and with my math schoolteachers.
Math is hidden everywhere in the daily life, but nobody notices it. I have always enjoyed finding interesting math themes in the daily life. Most people might say that the boomerang is about physics or aerodynamics, not math, and direction of writing is about linguistics, not math. For me, whatever I feel or think is math, or can be math. There is Math of Egg Shapes, Math of Fans, Math of Languages and so on. Math is unlimited! We, teachers and kids, have to go out from math textbooks and into the world.
I started to ask questions about boomerangs when I was 10 years old, and started to study Math of Boomerangs at 30, in 1978. In the summer of 1978, it was very hot. I had blinds on the windows, and researched blinds in an encyclopedia. The article about boomerangs happened to be on the same page. It brought back questions I had at 10, and I felt studying boomerangs would be more interesting than studying blinds.
To spread the word about fantastic boomerangs all over the world, I wanted to translate instructions for making boomerangs into 70 native languages. English is a common language, but only 20% of world people can read it. After translations into 70 languages, my interest changed from the Math of Boomerangs to the Math of Languages. How do the ways languages evolved relate to the ways people write? This theme is very exciting for me.

Picture: a screenshot from Yutaka Nishiyama’s site. His new book includes the first thirty articles from this collection – The Mysterious Number 6174: One of 30 Mathematical Topics in Daily Life.
What activity can a family or a math circle do with children, about their native language and math?
Almost all people in the world only know their native language, and believe their language is correct and excellent. Ask kids what is the correct direction of writing. They are likely to answer about their native language. Then you can discuss how there are hundreds of languages on this Earth, and knowing different languages and cultures is useful for world peace. English is written left to right, Arabic right to left, but which is correct? There is no right answer for that question!
In our upcoming book Bright, Brave, Open Minds by Julia Brodsky, there are dozens of “Aha!” problems that sound easy, but lead to wise or funny insights. Yutaka Nishiyama’s simple question, “What is the correct direction of writing?” is a great example of an easy task that leads into deep insights. – Maria D.

In the Boomerang Project kids learn to make their own boomerangs. How can kids experiment and play around? What variations and variables can they try?
For kids, paper boomerangs are easy to make and safe to fly. Here are some variations:
- Make two copies of the same boomerang and glue them together. How far will that double boomerang fly, compared to the single?
- Make holes at the end of wings. You can hear the whistle. Try different holes.
- Make alphabetical boomerangs, in shapes of letters from A to Z, or the first letter of your name. Whose boomerangs can return the best? X or Y return well, but I does not. O is stable to fly but does not return so well, and so on.
Posted in A Math Circle Journey, Make
Live online events, 1001 Circles, Math Storytelling Day: Newsletter September 2, 2014
Subscribe and read archives
Pinterest | Twitter | Facebook | Google+
Hi, I am Moby from the Moebius Noodles project, bringing you the news about Natural Math. Send me your questions, comments, and stories of math adventures at moby@moebiusnoodles.com

In this newsletter:
- Join us September 3 for a live online Math Future event with leaders of Proof School
- 1001 Circles: five newest interviews with leaders
- Stories for the Math Storytelling Day, September 25
Math Future live online event September 3: What if you could design a school any way you want?
Imagine like-minded parents, teachers, and administrators who deeply care about math. Imagine hundreds of years of their combined experience running math circles, math Olympiads, and family mathematics. Imagine freedom to design the best school you can for the kids of that community. This is what Proof School is about!
Join the open, free online event in the Math Future series. Meet the founders of Proof School, a radical education innovation for children who love math. Listen to a short presentation, chat with people in the audience, and ask presenters questions.
1001 circles and leaders
Try a math circle activity with your kids, or check out what keeps math circle leaders inspired! We are interviewing math circle leaders, experienced and new, with groups large and small, from all over the world. Here are the newest stories in the 1001 Circles series:
- Train your robot with DrTechniko
- An environmental geologist wants to save the world, runs a Math Club
- Jane Kats on game circles and family math camps
- EuclidKids LLC begins as a friend helps a friend’s 5 year old
- Dad and son organize Raleigh Advanced Science Club



If you run a math circle or a family group, or want us to interview a friend who does, email moby@moebiusnoodles.com and we’ll add your story to the 1001 Circles showcase!
Math Storytelling Day September 25: send us your stories!
Celebrate Math Storytelling Day by sharing your math stories, big or small. One in every 20 people who submits a story before September 25th gets a Math Maker t-shirt.

Our first story this year is about a dad who shared his fascination of cost-benefit analysis with his 6-year-old and their friends. They set up a pretend casino, found ways to rig games, and… Well, I will let Stephen Taylor tell you all about their adventure: The day my first grader fell in love with numbers.

Sharing
You are welcome to share this newsletter online or in print.
Talk to you soon! Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter
Math Storytelling: The Day my First Grader Fell in Love with Numbers
Stephen Taylor first wrote about Zometool adventures for our 1001 Circles series. Now Stephen shares a more personal story, to celebrate Math Storytelling Day on September 25.
For some, the love of mathematics grows gradually, over time. Other people experience love at the first sight of a math game or a tricky puzzle. Many grown-ups who love math, if you only ask them for their math story, can trace the feeling to an initial obsession with a single activity! Read Stephen’s tale to see how parents can notice, support, and nurture these feelings…
I have two young kids, now 6 and 8 years old. My wife and I have put much effort in teaching our kids from a very young age. We threw out the TV, and have played numerous games with our children. Like Maria Droujkova, we believe that what you learn as a young child you learn incredibly well, in a very natural manner, and that it will serve you through life. We also believe that teaching with love, kindness, and lots of involvement is not a chore, but fun for the parents as well as the kids.
As we get older we cannot but absorb the built-in assumptions of the society. We now watch our kids enter school, and see both the value of our efforts, and also how the opportunity for them to learn freely is quickly taken away by the school system. My particular goals have been to teach my kids the concepts and vocabulary of knowledge, easy and fluid methods for learning, and a love of learning and problem-solving. Imagine my dismay when midway through the first grade, I noticed my 6 year old Kai did not really love arithmetic and numbers! The games we had played had been mostly conceptual, with a lot of pattern recognition, such as Chess, Traffic Jam, Chinese Checkers, Mastermind, Pentago, Blockus 3D, Lego, and Zometool. So I got to thinking about number games, and remembered how as a kid loved to play roulette.
I bought an inexpensive used roulette set. When my kids became sufficiently curious as to what was in the package, I opened it up and started playing with my family, the neighbor, and his two kids. I do not believe in teaching formal rules before the start of a game. I just let the kids learn the rules along the way – kind of the way they learn a language. I soon found that the kids absolutely loved the thrill of the spinning ball, the sorting, grouping and counting of their chips, and the simulation of the casino environment. Yes, I hammed it up a bit: calling “no more bets” as the spinning ball started to slow down, and offering free drinks to players who had just suffered a loss – this one caused shrieks of delight! In turn, I was delighted to see the children’s fascination with the pace of the game, winning and losing according to the spin of the wheel, their choices of bets, and their effortless understanding of the numbers. I must add that along the way I did coach them on the evils of gambling and casinos. My kids now know you are highly unlikely to win big in a casino, and if the casino sees you winning too much, you are summarily thrown out – how unfair!
The game of roulette has three concurrent number systems running at all times. First, there are the numbers 1-36, 0, and 00 on the wheel itself. They are selected at random by the spinning ball that drops into one of the 38 wheel slots. Second, there are the corresponding 38 numbers on the mat, and their many categories: black and red, odd and even, rows, thirds and halves of the board, and finally the zero and double zero. The last two tilt the game odds in favor of the house. Third, there are the players’ and casino’s chip counts, going up and down with random winning and losing.

I was not able to teach the kids the finer details of the probability of winning and losing, but they certainly got the gist of it by trying different bets and observing the outcomes. For example, a good exercise is to blot out the zero and double zero and then have kids place equal bets on red and black, odd and even, or each of the 36 numbers. They soon see that under such a system the total chip counts of the players and of the house remain constant. Under that system, at each turn players’ gains (that is, house’s losses) from the winning number equal total players’ losses (that is, house’s gains) from all the losing numbers. However, when you uncover zero and double zero, the house start to win.
After playing the game for a couple of weeks, I said to Kai: “Let’s see if the wheel is off balance, and if we can figure out how to beat the casino”, which, in his mind, meant beating his friends, sister, and mom. One Sunday morning, while everybody was out, we started to spin and spin the wheel and record the results. My son had just learned how to tally, so he was the scribe. He quickly realized what we were trying to do, and it produced great motivation, especially after he saw that certain numbers come up more frequently. After all, it was just a toy wheel and not very well balanced. At his insistence, we spun the wheel nonstop for two hours, while he kept track of how frequently numbers came up. What better number practice can you get? Kai developed his own little system for counting the frequency of numbers. It wasn’t the most efficient system, but it was original, and it worked. We also plotted the numbers in a simple visual way, which he totally understood – and how could he not? You can see his workings in the figures below.

Professionally and personally, I am very interested in probability and risk applied to games, investing, and designing large facilities. In such situations, one has to understand the risks of events such as floods and earthquakes, and the costs and benefits of reducing these risks. I feel that sharing my knowledge and interests with my children (and my friends’ children) is a core parental responsibility. To see kids grab that knowledge, even tacitly through a game, is thrilling. It adds value to my years of study and, yes, it strokes my ego. What’s more, almost every time I play a game some kid comes up with a startlingly fresh and unusual approach and I end up learning too.
As the pattern emerged clearer and clearer, Kai realized that we were onto something very valuable. Thus our important findings were to be kept secret, so that he could beat his mom and 4 year old sister when they came home. He memorized the 8 or so best numbers and then hid the recording book. I wasn’t sure yet if we had a strong enough winning formula. Later it turned out that we had a good advantage over the house, which became huge when compounded turn by turn. I also knew I was favoring my son like a deus ex machina, but he had to see his effort rewarded. For all his research effort, he got to play the central stage in a performance that could surprise, delight, and enlighten others.
When my wife and daughter returned, out came the roulette set. Because of the potential for gambler’s ruin (a random string of bad luck), I dealt out 50 chips, rather than the usual 30 chips we had previously dealt, and off we went. Lo and behold, the wheel was off balance enough for Kai’s system to work. With a sufficient buffer of the initial 50 chips and a good edge in probabilities, compounding turn by turn, Kai was soon in the money, betting heavier and heavier following his intuition, and winning more and more chips. (See William Poundstone’s book Fortune’s Formula for optimizing bet size according to your edge.) Eventually, Kai broke the bank and held all the chips. My wife, still in the dark, was astounded: she had no idea that the boy had “rigged” the game!
All the while Kai had been zealously sorting, counting and grouping chips of various denominations, watching the spinning numbers, correlating these to his bets on the board, thinking of better strategies, thinking of how much to bet, watching the casino’s money, and lending money to his mom and sister as the casino broke them. His mind was full of numbers. Spin by spin I could almost see new synaptic connections being made in his brain. His strategy was improving. This went on for two hours, and this after two hours earlier in the day spinning and recording! My wife, daughter, and I were also having fun. Yes, everyone was having hours of fun with numbers, and my first grader had spent 4 hours in one day doing just arithmetic – without any coercion!
The game went on so long that eventually we had to send the kids to bed. This involved packing up and taking away Kai’s huge winnings. This did not go down well, and he was in tears. I did not realize how strongly attached he was to his chips, and I was perturbed at this attachment. Was I teaching my kids to become obsessed with money? Kai’s tears soon dried up as he just had to tell his mom and his sister how he had won at roulette. Kai brought out his recording book and everything was explained, which was another proud moment – and a math exercise.
Of course after this game of roulette we had to play the game again and again. Our neighborhood friends and their mothers, uncles and aunts, and everyone was invited to play. The family had been sworn to secrecy. Kai was a hero and people said that they wanted to take him to Vegas on their next visit. I always countered this by whispering in his ear that the casinos use well balanced wheels, and if they did see him winning big, they would take him into the dark back alley and rough him up. He seemed to get the message as he would repeat it. (See the fascinating History Channel documentary Breaking Vegas – The Roulette Assault, where an out of luck family develops a system to determine the off balance of casino wheels to win big and how they are roughed up and eventually broken by the casinos.)
How did people enjoy Kai’s “show”? His sister picked up on the excitement, and wanted to spin the wheel and record the bias too! I usually explained to the neighbor parents what Kai and I had done fairly early, so they knew it was about experiments and learning, rather than cheating. They were accepting of “those things nerdy engineers without TVs do with their kids.” Usually Kai would show the other kids “the trick” quite soon after demonstrating he could win. They often struggled to understand, not having spent hours spinning and tallying. When the kids understood, they immediately wanted to use the trick to beat their parents! None of the kids were upset with Kai. On the contrary, they showed appreciation for sharing his trick.
After a while, I bought another toy roulette wheel and waited for the next game of roulette, cunningly positioning myself as casino’s banker. As expected, Kai used his system to soon have more chips than anyone else, at which point I announced: “The casino is not stupid”, and pulled out the new wheel. Kai was shocked and was not sure what to do. He continued betting his system on the new wheel, which was highly unlikely to have the same imbalance as the old wheel. Soon the house odds knocked him down and ate up all his earnings. He was not happy with this little game of life that I had inserted. In fact, he was in tears. Yet he soon recovered, and set out to find the bias of the the new wheel.
I experience a lot of emotion and worry in choosing approaches to teaching my kids. I have had to work very hard to understand my children’s personalities and their boundaries between fun learning, and frustration or anger. Although learning does seem to continue even during bouts of frustration and anger. I feel good seeing tremendous progress in my kids’ mental abilities, a strong attachment to me, and a desire to learn. If left to themselves, kids bounce back quickly from frustration and anger, so by feeling blue about it, I am not helping them or myself. I remember my own frustrations as a kid; now I believe it is a part of learning, not necessarily bad. It is interesting to note that some Asian cultures are much more inclined than we are to give their kids difficult problems and let them be frustrated. I mostly, but not always, avoid pushing the hot buttons and crossing the frustration boundary. I also delay difficult discussions to a point at which the discussion can be rational and unemotional.
From this experience my son saw utility in numbers. The amount of arithmetic practice from the gazillion games of roulette and wheel spin tests helped him surge ahead. Since then we have found that other games with numbers, such as card games, dice games, and Monopoly, are a good way to teach our kids arithmetic. I still prefer the concepts and have not stopped teaching those. But arithmetic is important too: it helps the kids do well at school and to feel good about their skills. I don’t think that my kids will be attracted to gambling as they grow older: the novelty will not be there, and they now have the inside knowledge coupled with the stories they have heard from me about the evil casinos. Kai quickly grew to lose his attachment to his winnings. He can now win or lose and move on. Roulette is no longer a favorite game, but it was a great teacher. Kai’s love of numbers has not waned and over time he has become very strong at arithmetic. Mathematics has been his favorite subject at school since the middle of first grade and one memorable day.
Posted in Make
1001 Leaders: dad and son organize Raleigh Advanced Science Club
David Handy is a computer engineer and a homeschooling dad of four. He started a math, science, and programming science club to help youth, including his son Evan, to succeed in challenging technical studies in college, in their careers, and in life. Here David gives an interview for the 1001 Circles series.
In our 1001 Circles series, we feature math circles stories from the point of view of a circle leader, who acts as an invisible tour guide. In the companion series 1001 Leaders, we put the spotlight on the leaders themselves. What got them started and what keeps them going? What are their math dreams and worries? If you lead a math circle, an engineering club, or an informal playgroup, we would like to hear your story or interview you. Write moby@moebiusnoodles.com to talk about your adventures.

Photo: David at the Raleigh Maker Faire, with the elevator tower the club presented there.
What made you decide to organize a club for your son?
What started us down this path was when Theresa and I decided together, before our first child was born, that we would homeschool them. We work together as a team. She designs the main curriculum and does the more day-to-day supervision, and I fill in special needs that Theresa does not feel comfortable with (such as high school science) and do special projects, the science club being one of them.
I have tried a variety of activities with my children over the years, some more organized than others. When Evan was younger, I worked with him to develop a computer game called Bug Blast. The game was never “finished”, but we had some good times together. Evan created an outrageously humorous animation of a frog eating a bug – chewing and swallowing!
Evan’s older brother Nate actually gave me the idea of a science club. When Nate was age seven he formed his own little club of neighbors and friends and called it “Science Group”. Seriously.
Where can we see some of your club’s work?
The students in our club built our club’s website themselves using WordPress. My son Evan installed WordPress on the Linux server and configured it himself. Students in the club authored all of the content except for a couple of pages owned by me. And here is the link to the description I sent to parents of prospective students via spice-line (a local homeschool email list). We didn’t do everything described on this page, but we did most of it. We showed off projects publicly at the Raleigh Maker Faire.
The main modification I made was to make our projects way simpler than what I originally had in mind. If I had been working with only 4 or 5 students I could probably have done more advanced projects than what I could do with 9. I updated the “Time Commitment” section to reflect what actually happened vs. what was originally planned.
Here is a quote from the document, with some of the club’s principles:
4. Acquiring real knowledge and experience is the purpose of our class. Getting better test scores is a likely side effect but not the direct goal. “Teaching to the test” results in erasure of knowledge from the student’s brain as soon as the test is passed. We will avoid that pitfall.
5. The requirement to demonstrate skill in mathematics, especially Calculus, is the narrow gateway that excludes many from the sciences and engineering. We intend to remove the mystery of Calculus and blast that gate wide open for our students.
6. Calculus was invented by Newton to solve real Physics problems and to describe the behavior of the natural world. We will go against the trend of most textbooks that teach Calculus in isolation, but instead we will demonstrate a use and a purpose for each new mathematical principle we learn.
7. If you learn a principle and immediately apply it to some purpose meaningful to you, you will probably remember it forever. We intend to apply what we learn in hands-on projects.

Photo: seven of the club members by the elevator tower; Evan is in the back on the right, in the red shirt with a circle.
And here is the overview of what members of the club were to learn in their unit studies:
- The Scientific Method
- Modeling Physical Systems
- Modeling in General
- Try Before You Die, or the Genius of the Wright Brothers in Making Model Gliders Before Trying To Fly Themselves
- Mathematical Modeling
- Einstein and Thought Experiments
- Equations
- Numbers
- Computer Simulations
- Standing on the Shoulders of Giants
- Benjamin Franklin
- Isaac Newton
- Maxwell and Faraday
- Thomas Edison
- Nicolai Tesla
- Orville and Wilbur Wright
- Albert Einstein
- Werner von Braun
- Philo Farnsworth
- Modern-Day Pioneers (Guido van Rossum, Steve Wozniak, others…)
- Foundational Principles
- The First and Second Laws of Thermodynamics
- Newton’s Laws of Motion
- Basic Electronics
- Ohm’s Law (V=IR)
- Kirkoff’s Circuit Laws
- Capacitors
- Inductors
- Intermediate Electronics
- Operational Amplifiers
- Oscillators
- Applications (Projects)
- Rockets
- Robots
- Radios
- Control Systems
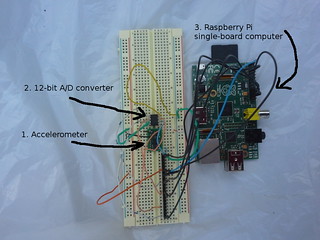

Photos: The accelerometer device student wired with a Raspberri Pi computer. It was mounted at the bottom of the elevator cage of the tower.
How did you plan the club?
I was looking at two things: Evan had only one more year with us before finishing high school and going to college, and he had told me that he wanted to be an inventor some day. I had sort of a “bucket list” of things I wanted to do with him before he started a challenging engineering or technical course in college. Those were things that Evan might not have known to ask for, and that retrospectively I wish I had done before I left for college. That was my state of mind as I planned our science club.
But after we got underway, the situation changed. Our church recently changed its policies to allow young men to begin missionary service at age 18 instead of age 19. Evan announced that he wanted to leave for his mission at the earliest opportunity, and he turns 18 in August of 2014. Evan graduated from our home school in Dec. 2013 and began working and earning money for his mission. He was accepted to the college of his choice (BYU-Idaho) and then deferred starting college until after his mission. The net effect was that Evan was very engaged with the science club the first half of the school year, but much less so the second half, as his work took priority, and college was no longer on the immediate horizon (though definitely still there in his future!)
This is what I meant when I said earlier that things didn’t work out like I planned. Life happens! So then the science club for me became more about mentoring an amazing group of people in the community, a self-selected group of very interested teens and very supportive parents. Evan has a friendly, outgoing personality. He participated in all of our in-person meetings the second half of the year, even though he missed most of the online meetings. He is the oldest student in the club, and I think the others look up to him.
Question to Evan: What can you say to a teen whose parent is willing to help build a club like that?
I would tell the teen to be enthusiastic about it; help out and don’t complain. From my perspective, several times I helped out when something needed to be explained to the whole class, and half of them weren’t getting it. If I understood the topic that my dad was talking about, I could explain my view-point and help the others understand the concept. If I did something like this again, I would try harder to stay alert during the morning calls and get more involved in the projects (i.e. make a few python programs for the website). I had a lot going on in my life during the last half of the class, so I wasn’t as involved or enthusiastic as I would have liked, especially since work made me miss most of the morning calls.
Back to David. Imagine parents who are planning their very first math circle or science club. What advice do you have for such newbies?
You have to give in order to get. You can recruit people whose strengths match your needs, but in turn you need to give of your time and talents to others as well. In helping other families you can help your own.
Find other families with common interests.
Don’t try and do everything yourself. The other dads in the group stepped up and helped a lot at the end. I should have asked them sooner.
How can a student organize and create a structure for learning and prepare, if the student doesn’t know the subject yet (catch 22)?
Google is your friend. But you need other friends as well. Make friends with adults who know what they are talking about. You would be amazed at how many of them will want to help you. They may be too busy to teach you everything, but they can point you at what to read.
Is it hard for different generations to work together? What about genders?
To me the highlight of the science club was our final meeting the Saturday before the Maker Faire, when we put all the parts together. We had 4 dads there, including me. There was a father showing his son how to solder a connection, another father and son team getting their Arduino project working, and another father and son programming together. Some great generational learning going on!
All the applicants to the club were boys, although it was not my intention to limit the class to boys. Next year, my experience changes. For the first time since I started teaching homeschool science, my students will be mostly girls, including our oldest daughter, age 14. I’ve been reading up on gender differences in learning, and trying to prepare. One challenge I intend to take on is that some of the girls in this Chemistry class “don’t like science” and “aren’t good at it.” Maybe we aren’t all Einsteins, but I think everyone is capable of appreciating science and succeeding at their own level. I’m hoping to get some people more interested in science.
Wish me luck!
Posted in A Math Circle Journey, Grow




