“Adventurous Math” on Kindle; what is multiplication? Newsletter February 17
Subscribe to Moebius Noodles newsletters
Pinterest | Twitter | Facebook | Google+
I am Moby Snoodles, and this is my newsletter. Send me your requests, questions and comments at moby@moebiusnoodles.com

Book news
Adventurous Math for the Playground Crowd is now available for Kindle and other e-readers in the .moby format.

What is multiplication?
Questions, comments, ideas, blog posts about multiplication are coming in for the project that starts with our online and local Math Cafe on February 18th. @twen1977 and quite a few others ask about memorization:
Is there a better way to learn multiplication tables besides just memorizing?
Yes, yes there is! We will be addressing this and other parent and teacher questions during the Math Cafe, and throughout the multiplication project. Meanwhile, head for the blog to check out the variety of posts that bridge multiplication and other human endeavors.
Marina Mersenne presents an advanced theater game, The Mirror Routine – easy enough for toddlers to learn, complex enough for professionals to use. Of course, symmetry is one of the major models of multiplication.

Malke Rosenfeld invites you to share memories of Beautiful Objects from your childhood, using a hands-on manipulative about group theory (hence multiplication!) as her example. Alexander Bogomolny, a mathematician and math educator of Cut-the-Knot fame, responds with a touching example:
Puddles, I was absolutely taken with the puddles. The surprising thing was that an object’s reflection moved when I moved while it was not mine but the object’s.

Yelena McManaman shares an invention of her son Mark (7), who found a way to model fractal stars with mirror books: a combination of two models of multiplication in one beautiful project.

Mark Gonyea gave us an interview about his artistic 100-charts, with many cells built on arrays, fractals, symmetry and other multiplication patterns.

The Natural Math crew added new finds to our big history of the Multiplication Tower, a slightly mysterious 3D-modeling project that people have been independently reinventing since the 1970s.

In response to examples made of wood, LEGO, beads and more, we got two fresh versions. The history continues to grow: after our story came out, Jenny’s son Viktor built his multiplication towers in Minecraft, and Sheryl Morris remixed the bead version in Montessori colors.


Sharing
You are welcome to share the contents of this newsletter online or in print.
Talk to you in two weeks! Moby Snoodles, aka Dr. Maria Droujkova
Posted in Newsletter
Mirror book fractal stars
Yelena McManaman’s son Mark loves deep ideas. Yelena writes: “Mark is obsessed with the idea of symmetry and infinity. Now he’s also trying to build up on his “zero infinity and infinite zero” ideas.” In one of his latest experiments, Mark invented a way to model fractals with two mirror books.
There is a chapter on fractals and another chapter on mirrors in our Adventurous Math book, but I’ve never thought of combining the two ideas! This is a great example of why we need children in our workplaces and creative projects. Young kids are great at divergent thinking, unexpected connection, and noticing details. Imagine the worlds where engineers and scientists developed a way to consult Mark and other young kids during explorations.
Here is Mark’s fractal star, with four rays made out of double pencils. Note how both mirror books are opened at 90 degree angles, to make four copies.

After Yelena sent me this cool photo, I just had to make my own mirror book fractal stars! I played with three-ray stars and five-ray stars.


When kids draw fractals by hand, they often use new color for each new level. I colored levels of my five-ray fractal in Photoshop: the first level stayed the original orange, the second level is yellow, and the third level is green.

This is how the setup with two mirror books looks from the top. You can only see a few levels of the fractal from that angle:

You can get small mirrors in craft stores, and large mirror tiles in home improvement and hardware stores. Invite your kids to join Mark in his experiments! If you want to share your mirror book or other fractal creations, email me your photos – moby@moebiusnoodles.com

Posted in Make
One to one hundred: a series of posters from Mark Gonyea
Mark Gonyea is an artist and graphic designer who recently crowd-funded an inventive and elegant series of 100-charts. The artwork caught my eye because the patterns were both adventurous and algebraic. Want to borrow my math goggles? Go on a scavenger hunt within the posters to find these mathematical structures:
- Arrays
- Star sheafs and star polygons
- Fractals
- Tessellations
- Mirror and radial symmetry
- Randomness
My finds (and the brief definitions of these math terms) are at the end of the post. What else do you see in the posters?

I sent Mark a few interview questions.
— Do you remember how math was for you when you were a little boy?
— I remember being good at math. I liked Algebra the most, which when I think about it is not unlike graphic design to me. It’s adding, subtracting, dividing and multiplying. It’s all about trying to solve a problem.
— What feelings drove you to create that many complex hundred-charts? What’s the story of this project, and the meaning of the story for you?
— I started creating multi-panel posters around the year 2000 as a reason to exhibit at the San Diego Comic-con. So at first, they were very much narrative and kind of a long comic strip in nature. Fairly quickly I started to do more design focused posters as well and a few years ago one of those posters was reprinted in an art book about abstract comics. The piece was a 48 panel comic called Squares in Squares where each panel pulled back to reveal more and more squares surrounding each other with no narrative other than the increasing complexity of shapes. So when I started to think about what kind of Kickstarter project I wanted to do I thought back to the popularity of that poster and it really got me thinking of doing a series of sequential designs.
— Can you give a few design tips for families and Math Circles creating their own artistic number charts?
— Definitely start small. I realized pretty quickly how complicated things can get, even before I got to the larger numbers. With the first 1 to 100 poster (Shapes) I think it was actually #14 where I realized “Oh, this is going to be more involved than I thought” and that number became my first asymmetrical panel.
— Where can we find your work online?
— MarkGonyea.com is the best place to see what I’m up to and where to find my work online. Thanks!


Here are examples I found. It strikes me that many of them have to do with multiplicative reasoning: grids, symmetry, and fractals for sure! What other math ideas do you see here?

Posted in Make
Multiplication Towers
Check out activity ideas, adaptations by ages, and even more examples of Multiplication Towers (plus 14 other awesome topics):
Multiplication Explorers Self-Paced Course
One of the wonders of the ancient times is that many tribes and nations from different continents independently discovered and built patterns we call Labyrinths. Some math ideas are universal like that! Over the last decades, the Multiplication Tower idea has been appearing in many different projects. We interviewed authors from the 1970s to early 2000s, and it turned out they came up with the idea independently! But for the last few years, we’ve all been talking to one another, directly or through our blogs. Kids and their grown-ups build multiplication towers using many kinds of materials: wooden blocks, LEGO bricks, software and 3D printing, and beads.

This page documents the appearances of multiplication towers. If you build a tower or know of an example we missed, please send it to moby@moebiusnoodles.com
2013 Moebius Noodles
We have a chapter on Multiplication Tower games for young kids in the Adventurous Math for the Playground Crowd book. It summarizes ideas from many other projects on this page.
2013 Malke Rosenfeld
In a blog post with many quality photos and thoughts on commutativity, Malke shares her easy-to-make, beautiful version of the Tower.

Malke writes: “When we started building this tower the questions started flooding in. I started wondering about a LOT of things…” Indeed! So will you wonder, if you build the tower.
2013 Sarah Dees

In her blog post, Sarah included detailed instructions and her thought about the design. She writes: “The finished graph lends itself to interesting observations if you look at it from different angles. I ordered the blocks from the Pick-a-Brick section on lego.com. We have invented several math activities with these bricks (more posts to come!), and it has been totally worth the cost.” Sarah’s activity was inspired by Malke’s beads.
2013 jmommymom at Highhill Homeschool

What a creative way to replace materials! The blog post explains: “We didn’t have a foam block, so we filed a cardboard box with cotton to serve as our base. Then we stuck in wooden skewers in a 5×5 grid pattern, and added beads to that corresponded with the multiplication tables.” This activity was inspired by Malke’s beads, as well.
2013 Andrew Staroszik and Roman Hegglin on Thingiverse
In 2013, several tower model appeared on Thingiverse, a 3D printing site. You can use these files to print your own towers.

Andrew’s tower was originally inspired by Michael Punzak’s wooden model we describe below.

Roman’s tower comes with captions in Roman numerals and Braille. It’s also made of thin tiles rather than cubes. These two features make for more formal or abstract remixes.
2010 Brenda Weiss
Brenda is a physicist and a creative parent. When her son Corbin set out to make a multiplication table with Cuisenaire rods, he built the first set of towers on his own. Brenda writes: “In ‘helping’ make it symmetric, I ended up knocking over most of what he had built. We built this together. Corbin was responsible for the multiple block levels, as I couldn’t balance more than two blocks.” It helps kids to know they are giving real help. Take a page out of Brenda’s book: be open about the areas where you need help.

2010 Colin Graham
Colin made a collection of 20 math adventures with LEGO, modeled with the free Digital Designer software, and invited colleagues to add more ideas. Here is the multiplication tower from his collection.
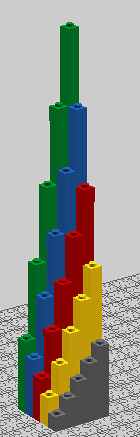
2007 Studio 1:1
The design studio from Gdansk, Poland made this giant tower and took several artistic photos of it.

2004 and up, Maria Droujkova’s Math Circles
Five Math Circle kids built these LEGO towers on a chessboard in 2010. The story was that each block was a creature (hence the smiley faces) that kept growing from row to row.

Later in 2010, the same Math Circle built a model with a cereal box and bamboo skewers. The picture shows the 3 by 4 array with pencils. The skewer in the lower right corner of the array sticks out by 12 units, that is, 3×4.

The above model was inspired by the Kinetic Structure BMW installation:
An earlier picture, from 2004, shows two kids from a Math Circle building with LEGO on a poster board.

2001 and up, Dor Abrahamson and friends
In 2010, Dor wrote: “Multiplication Tower as an Object-to-think-with.” Well put! Check out Dor’s page about 3d multiplication, with more pictures, at his Embodied Design site at University of California, Berkeley. This six-foot structure made of wood was constructed by Michael Bryant, one of Dor’s graduate students.


In 2005, when 3D printers were still rare, Paulo Blikstein printed this model at Uri Wilensky’s lab. Here is Dor playing with the Tower. Paulo now leads Transformative Learning Technology Lab at Stanford.

Here is a third grader building the multiplication tower from plastic blocks and play-dough in one of Dor’s experiments in 2001.

That was the year Dor designed the tower, first as a 3D output from a spreadsheet. Here is that historic document.

1988 and up, Michael Punzak, Michael Gleason, Douglas Shult, and Joshua Tenenbaum

Michael writes in commentary to his page of lovely hands-on explorations into patterns: “I made my first model about 20 years ago. It was inspired by an article and photograph in The Mathematics Teacher (Shult, and Tenenbaum, 1988: A three-dimensional multiplication table inspires mathematical discovery). I found this first model, which is about 3 feet tall, a lot of fun to paint (about 10 coats of acrylic, to get a metallic look to it) but very heavy to schlep around. I commissioned a friendly carpenter, Michael Gleason of Newton, MA, to build a smaller (about 18 inches tall) model, which is much lighter. I also use a 5-by-5 multiplication table model built with LEGO blocks for volume and surface area challenges. It is surprising and a bit disappointing that so far my 4-6 graders (a STEAM) after school class in Needham, MA, have not made the necessary jump from the 5×5 model to the 10×10 model.”
1975 Don Cohen
In the oldest multiplication tower we found, the layers were cut out of wooden Dienes blocks by Don. He has kept it around for his students to build up the layers and to find more patterns. His camera wasn’t good at close shots, so the numbers here are written over the picture. Check out Don’s work on calculus by and for young people!

Happy tower building!
Posted in Grow






