Today, our guest is Joey Grether, an unbridled idealist, parent, and teacher. His journey to math play with kids started with designing tools and devices. Have you ever wondered how Montessori designed all the activities with her beads, or how Cuisenaire came up with the base ten rods? Here is Joey’s story about a colorful multiplication wheel that helps children and their adults explore factorization and primes. You can see how the ideas for student activities come up as a grown-up is playing, exploring, and designing.

In our 1001 Circles series, we feature math circles stories from the point of view of a circle leader, who acts as an invisible tour guide. In 1001 Leaders, the companion series to our 1001 Circles, we put the spotlight on the leaders themselves. What got them started and what keeps them going? What are their math dreams and worries? If you lead a math circle, an engineering club, or an informal playgroup, we would like to hear your story or interview you. Write moby@moebiusnoodles.com to talk about your adventures.

Updates:

1. The sites linked here still exist, though the products aren’t commercially available. We hope you can make something similar from pictures.
2. The Tesla connection was a hoax. You can see some discussion in the comments. Since the hoax was relatively benign, we are keeping the original write-up here as a memento/archive.

Hi there. I am a high school substitute teacher, graphic designer, and parent, with a degree in Cultural Anthropology. I have an 11 year old and a 3 year old. When the 3 year old was a little younger, I decided to work on a project that would combine numbers and letters. I sketched and struggled for a few weeks. One day I was impatiently waiting for something, looking at the clock as I was dividing up the letters for my project. I realized that if I combined the most used triads, ABC and XYZ, I could fit the rest of the letters in pairs around the clock. Once I did that, I knew how to fit other ideas into the circle: months, degrees, seasons, moon cycles, elements, the color wheel, and the music scale. I called the device The Learning Flower.

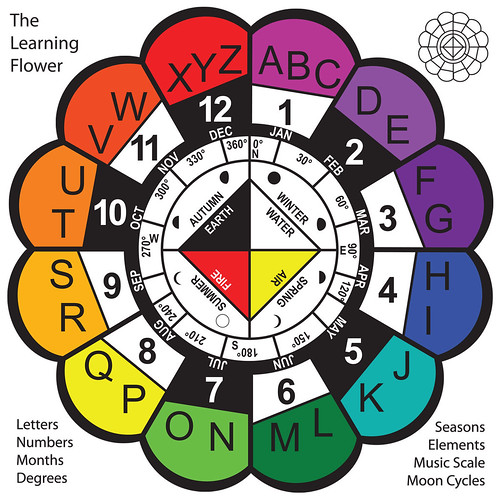
We have a lot of magnetic toys and puzzles around the house, so I made the Learning Flower into a vinyl magnet project. You can take apart the petals, and put them together again in a round cookie sheet. My 3 year old, Indara, would play with it on and off. Observing her and listening to other parents’ feedback, I made a simpler device with just colors, numbers, and letters. Indara seems to understand that one a bit better, because its middle disk supplies a picture for her to model. Here is a photo of another toddler playing with it, from a review at Tog&Glam blog.

I was showing the Learning Flower to friends. Some asked me where the math was, and I was kinda thrown back, thinking – math? This tool got 8 overlapping sets of symbols! Why add more? But then I tried anyway. It led me to develop a more complex device, adding days of the week, the periodic elements, and two more layers of numbers. As I played with the clock positions on my screen, patterns slowly began to stick out to me. First I noticed that 15 and 27 were in the 3 o’clock position, then that other numbers there were multiples of 3 too. Hmm… four positions (3, 6, 9, 12) contained multiples of 3, looking like a square. I started tracing other multiples. Then I saw multiples of 4 forming a triangle in positions 4, 8, and 12. Multiples of 2 make a hexagon.

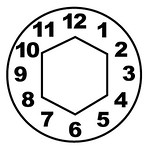
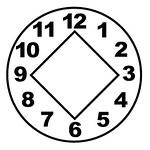
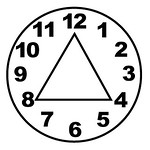
I sketched out the first 12 dozen numbers in a 12-position spiral, using the same positions of the clock. I then tried tracing the multiples of 2, 3 and 4. I noticed there were numbers that just were not part of the first few multiples. I worked on the diagram for several more days, fascinated by the simple patterns. I underlined the numbers that were not a part of the 2, 3, and 4 multiples systems. It turned out that they were primes. The rest of the numbers were prime! And as crazy as it sounds, this realization of how primes are distributed around the 12 positions hit me on 12/12/12! Were all numbers in these positions prime? Mostly. I checked prime lists online to be sure, and all were, except 25, 35, 49, 55, 65, 121… that is, the multiples of 5, 7, 11, and 13. The patterns began to feel more comprehensive.

Since then, I have been developing the device, trying to understand it, sharing it, and presenting it. I started calling it The Number Spiral, but people confused it with the Ulam Prime spirals. On different versions of posters, I call it Number Patterns, 12x Spiral, Web of Compositability, The Symmetry of Divisibility, and Grethers Spiral. Which name do you like the most? My pick and the name of my site is 12x Spiral, because it implies the design.

Why do numbers work like that? As I played with the 12x Spiral, I have developed a theory. For me, and for students using the 12x Spiral, answering that question is the most useful aspect of the device. It leads to figuring out where numbers are placed in each of the 12 positions, by combing the divisibility rules. Every number has a place, and if we can figure out that place, we can figure out what the number’s divisors are. Here are just some of the patterns students can explore while trying to answer that one Why question!

The theory is that numbers are self-organized around the smallest, most highly composite number, 12. The number 12 and many of its multiples (24, 36, 48, 60, etc.) are HCNs: highly composite numbers (with lots of divisors), which are extremely useful for measuring and proportions. Why are there 12 eggs in a carton, 12 inches in a foot, 12 months in a year, 24 hours in a day, 360 degrees in a circle, 60 seconds in minute? Because highly composite numbers can be divided evenly in many ways. For each 12 numbers in one ring around the spiral, there are 4 candidates to be prime. I started calling the 4 positions where these candidates reside the prime fields: positions 1, 5, 7, and 11. When two prime numbers are separated by just one composite number, such as 5 and 7, 17 and 19, or 29 and 31, we call them twin primes.

Here is another way to look at the prime fields. Recall the hexagon, square, and triangle that are the shapes of 2x, 3x, and 4x. The prime fields sit next to the vertical line between the positions of 6 and 12 o’clock, which is the shape of 6x. In other words, all numbers in the prime fields are either 1 higher or 1 lower than a multiple of 6. We also understand this as the equation 6x +/- 1 that, for natural x’s, works for all primes other than 2 and 3 (though not all results of the equation are prime). I found this equation online while I was researching prime number theory.

I like to draw these spirals in chalk or make wall murals. I tried this activity first with my kids, then as math workshops with their friends. I just start drawing a spiral, and color-coding the 12 positions. I make the spirals large, because kids love to run to clock positions or particular numbers when they seek patterns. As the spiral grows, students begin to see where numbers and colors belong. They jump in to help color and draw, making the mural bigger and bigger. You can also use found materials. Once we raked rocks in a dirt lot into a spiral. We invited kids to walk to its center, and to lay out rocks in a triangle shape (like bowling pins) to show more number patterns. Once you start drawing or building a spiral project, it can inspire many math and art extensions.

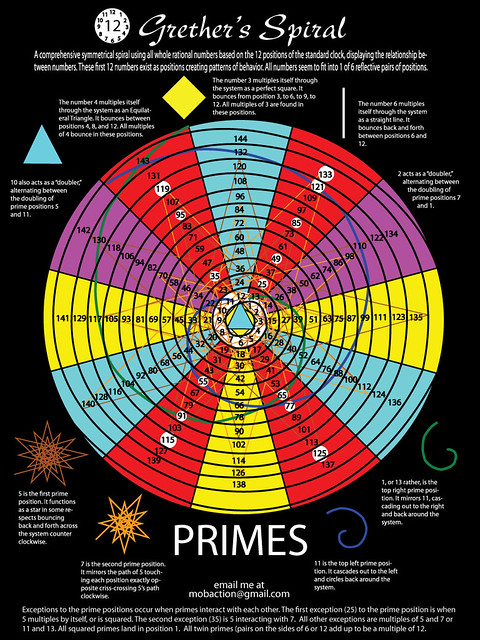
Now that we are looking at number relationships and tracing the web of multiples, we can explore more complex patterns. For example, let us define a way for numbers to intersect one another. Say, 55 is a product of just two numbers, 5 and 11. Looking at the spiral, mark the multiples of 5, that is, 5, 10, 15, 20, 25… Connect the numbers with lines. They will form a beautiful star. Now follow the multiples of 11, that is, 11, 22, 33, 44, 55… They form a spiral. The star and the spiral intersect at 55 and then at 110. Try it with other primes: observe how the stars and spirals of the numbers 2, 3, 5, 7, 11, and 13 intersect one another.  The stars and spirals relate to spirolaterals and Waldorf multiplication stars, but are also different, so you can explore them separately.

Here is another bridge to number theory, made visible by the 12x Spiral. When only two prime numbers are multiplied, or a prime is squared, we get semi-primes such as 35=5×7 or 49=7×7. The first non-prime exemption in the prime field is 25, which is a semi-prime, because it’s 5 squared. Want to know a neat pattern about primes squared? Find the first few on the 12x Spiral: 4, 9, 25, 49, 121. Starting from 5 squared, they all fall into the 1 o’clock position! In other words, all primes squared (besides 2 and 3) equal 12x + 1. Is it always true? How can you make sure without checking all the infinitely many primes?

Parents and math circle leaders who want to have a casual, easy math experience can start with checking the patterns of multiples. If you want to work with kids, draw the 12x Spiral with them! Or you can print the activity page I have created. Young kids can color, and older students can name each number’s divisors. The 12x Spiral poster is more of a reference, a way to invite math into the homes of kids.

Follow the multiples of 2, 3, and 4. See how their patterns become predictable. Then explore 8x, 9x, and 10x. For a more advanced task, seek links between patterns. For example, 5 and 17 are in the same position, next to one another. Are the patterns 5x and 17x linked? Let us find out! 5×2 and 17×2 are again in the same position, 2 rings apart. Look at 5×3 and 17×3. The same position once more, this time 3 rings apart. Ha. Awesome!

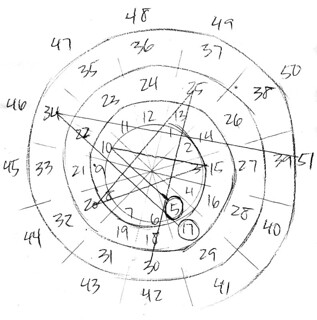
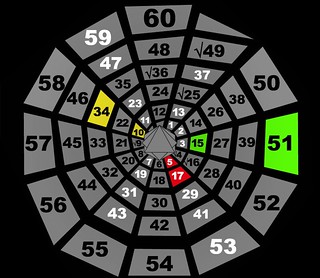
You can find patterns like this through simple, quick sketches. I would like people to get comfortable drawing this model, sharing it, thinking about it, and so, helping develop it! It doesn’t matter if our work is perfect, what matters is if we learn from doing it.

Up to now, we looked at positions to find numbers. The inverse game is more challenging: pick random numbers, and dial them in to the correct position on the spiral. The kids will eventually discover the strategy of using the divisibility rules (see below). For example, your number is 180. It is even (divisible by 2). Cut in half, and the result is still even (180/2=90): this means 180 is divisible by 4. The sum of digits 1 + 8 + 0 = 9, so 180 is divisible by 3. Since it’s divisible by 3 and 4, it’s also divisible by 12, and so it is in the 12 o’clock position. Do it for your birth date, your address, the current year 2014, whatever. Once you become more familiar with placing numbers into the web of compositibility, you will know their divisors at a glance.

Here are the rules of divisibility useful for these games. Knowing these rules, any number can be placed into one of the 12 positions on the spiral.

• If the last digit is even, the number is divisible by 2.
• Multiples of 3 have the sum of the digits divisible by 3.
• Halve a multiple of 4, and the result is even.
• If a number is divisible by 3 and 4, it is also divisible by 12.

The more you can understand how numbers relate, the easier it is to process them in your head. Say, you need 187 inches of 2×4 for a wall, but the store only sells it by the foot. How many inches do you need to add? How many feet will you need to buy? If you can visualize where the numbers belong, you know 187 is on the ring that is starts at 180 and ends at 192 in the 12 o’clock position. So you’ll need 192 inches, which divided by 12 gives you 16 feet. Many things use 12x as their systems of measure. If you go on a scavenger hunt, you will find examples such as 72 pixels per inch image resolution, or 12 packs of soda with 12 ounces each.

I have recently figured out how to make a simpler game. Print out the 12x Spiral poster for a visual reference, or draw the spiral using the first 36 numbers. Now take a pair of dice, roll them, multiply the numbers, and see how the result fits into the spiral. For example, if you roll 4 and 5, put the first die on the number 4 on the spiral. Now skip-count around the spiral by fours, as many times as the second die shows – in this case, five times: 4, 8, 12, 16, 20. There you are! 4 times 5 is 20. Another example: you got 3 and 6. Put the first die on the number 3. Skip-count from it around the spiral by threes, six times: 3, 6, 9, 12, 15, 18.

I’m sure there are many more ways to use the 12x Spiral, but I can’t figure them all out just by myself! Want to join? For more exploration, prompt students to look for patterns, try to draw some patterns of their own, or see what they notice about individual numbers. On that note, I am still developing this project and noticing new patterns. I am open to any and all ideas. Your and your children’s feedback will be greatly appreciated!

I believe the national math standard is to have 5 year olds know the first 10 numbers. What if I could get 5 year olds to know their number patterns (multiples) all the way up to 12×12? I think I can, but I need some support. The project is all about improving math literacy, and inspiring people to quit saying, “I’m no good at math, or art, or whatever.” Personally, I would love to teach kids that have rejected or are rejected by schools. It seems kind of ridiculous to me, but so far I have had a hard time getting people to understand and appreciate this project. Even educators seem hesitant to introduce the 12x Spiral. I think it’s because this is so new, while curricula are planned out months in advance and handed down from within the bureaucracy.

I would love to travel the world teaching any student of any age the web of compositability – with chalk murals, wall murals, or rocks even. I think this model is more useful than any multiplication table based purely on memorization. The 12x Spiral combines the multiplication table and the Sieve of Eratosthenes, allowing students to see how all numbers work together as patterns. It could resurrect many people’s interest in numbers, patterns, and math. If that’s too much to ask the universe at this time, I would just like more students to try it out. Maybe I could get a curriculum developing grant, or just sell a few posters to get young minds to explore the patterns. My ultimate lifelong dream is to run a 24/7 cultural recreation center.